《2025年小题狂做八年级数学上册苏科版提优版》

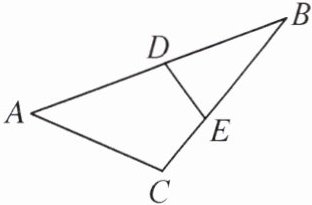
9. 如图,在△ABC 中,点 D,E 分别在边 AB,BC 上,连接 DE,AD= AC,ED= EC.
(1)求证：∠ADE= ∠C.
(2)若 BD= BE,∠B= 30°,求∠A 的度数.

答案：
(1)证明:连接AE.在△ADE和△ACE中，$\left\{\begin{array}{l} AD=AC,\\ ED=EC,\\ AE=AE,\end{array}\right. $所以△ADE≌△ACE(SSS)，所以∠ADE=∠C.
(2)解:因为BD=BE，∠B=30°，所以∠BDE=∠BED=75°.因为△ADE≌△ACE，所以∠C=∠ADE=180° - ∠BDE=105°.所以∠BAC=180° - ∠B - ∠C=45°.

1. 如图,AB= 2,BC= AE= 6,CE= CF= 7,BF= 8,则四边形 ABDE 与△CDF 面积的比值是(D)
A.3
B.2
C.$\frac{1}{2}$
D.1

答案： D　提示:因为AB=2，BC=AE=6，所以AC=BC + AB=8=BF.又因为CE=FC，AE=BC，所以△AEC≌△BCF(SSS)，所以$S_{\triangle AEC}=S_{\triangle BCF}$，所以$S_{四边形ABDE}+S_{\triangle CDB}=S_{\triangle CDF}+S_{\triangle CDB}$，所以$S_{四边形ABDE}=S_{\triangle CDF}$，所以四边形ABDE与△CDF面积的比值是1.

2. 如图所示的网格是由 9 个相同的小正方形拼成的,图中多边形的各个顶点均在格点上,则∠1-∠2-∠3 的度数为(C)
A.15°
B.30°
C.45°
D.60°

答案： C　提示:如图，可知AB=CD，BE=DE，AE=CE，所以△ABE≌△CDE，所以∠2=∠DCE.因为BE//CD，所以∠DCE=∠BEC，所以∠BEC=∠2，所以∠1=∠BEC+∠AEB=∠2+∠AEB=90°.因为∠2+∠3=∠DCE+∠3=∠HCB=45°，所以∠1 - ∠2 - ∠3=45°.

3. 如图,AB= AC,AD= AE,BD= CE,且点 B,D,E 在同一条直线上,给出下面四个结论：①△ABD≌△ACE；②∠ADE= ∠CAE+∠ACE；③AD//CE；④∠BEC= ∠DAE. 其中正确结论的序号有①②④.

答案： ①②④　提示:因为AB=AC，AD=AE，BD=CE，所以△ABD≌△ACE(SSS)，故①正确；因为△ABD≌△ACE，所以∠BAD=∠CAE，∠ABD=∠ACE，所以∠ADE=∠BAD+∠ABD=∠CAE+∠ACE，故②正确；根据已知条件不能证明AD//CE，故③错误；因为△ABD≌△ACE，所以∠BDA=∠CEA，因为∠BDA=∠DAE+∠AED，∠CEA=∠BEC+∠AED，所以∠BEC=∠DAE，故④正确.

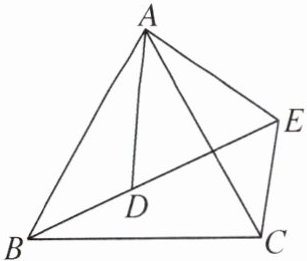
4. 如图,D 是四边形 AEBC 内一点,连接 AD,BD. 已知 CA= CB,DA= DB,EA= EB,则 C,D,E 三点在一条直线上吗？为什么？

答案： 解:C，D，E三点在一条直线上.理由如下:连接CD，ED.易证△ADC≌△BDC，△ADE≌△BDE，所以∠ADC=∠BDC，∠ADE=∠BDE.因为∠ADC+∠BDC+∠ADE+∠BDE=360°，所以∠ADC+∠ADE=180°，所以C，D，E三点在一条直线上.

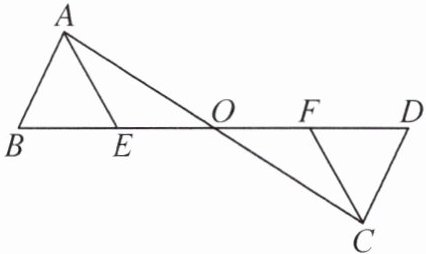
5. 如图,点 E,F 在线段 BD 上,BF= DE,点 A,C 在线段 BD 的两侧,且 AB= CD,AE= CF,连接 AC 交 BD 于点 O. 求证：
(1)∠B= ∠D.
(2)AO= CO.

答案：
(1)证明:因为BF=DE，所以BF - EF=DE - EF，即BE=DF.在△ABE和△CDF中，$\left\{\begin{array}{l} AB=CD,\\ AE=CF,\\ BE=DF,\end{array}\right. $所以△ABE≌△CDF(SSS)，所以∠B=∠D.
(2)在△ABO和△CDO中，$\left\{\begin{array}{l} ∠B=∠D,\\ ∠AOB=∠COD,\\ AB=CD,\end{array}\right. $所以△ABO≌△CDO(AAS)，所以AO=CO.