第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 估计$\sqrt{14}+1$的值在 (
A.2 和 3 之间
B.3 和 4 之间
C.4 和 5 之间
D.5 和 6 之间
C
)A.2 和 3 之间
B.3 和 4 之间
C.4 和 5 之间
D.5 和 6 之间
答案:
C
2. 下列整数中,与$\sqrt{(3-π)^2}$最接近的是 (
A.-1
B.0
C.1
D.2
B
)A.-1
B.0
C.1
D.2
答案:
B
3. 下列说法中,不正确的个数是 (
①实数包括有理数、无理数和零;②有理数和数轴上的点一一对应;③所有无理数都是无限不循环小数;④平方根与立方根都等于它本身的数为 0 和 1.
A.1
B.2
C.3
D.4
C
)①实数包括有理数、无理数和零;②有理数和数轴上的点一一对应;③所有无理数都是无限不循环小数;④平方根与立方根都等于它本身的数为 0 和 1.
A.1
B.2
C.3
D.4
答案:
C
4. 下列说法正确的是 (
A.$\sqrt{5}$是有理数
B.5 的平方根是$\sqrt{5}$
C.$2<\sqrt{5}<3$
D.数轴上不存在表示$\sqrt{5}$的点
C
)A.$\sqrt{5}$是有理数
B.5 的平方根是$\sqrt{5}$
C.$2<\sqrt{5}<3$
D.数轴上不存在表示$\sqrt{5}$的点
答案:
C
5. 实数a,b,c在数轴上对应点的位置如图所示.如果$a+b= 0$,那么下列结论正确的是(
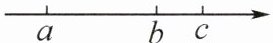
A.$|a|>|c|$
B.$a+c<0$
C.$abc<0$
D.$\frac{a}{b}= 1$
C
)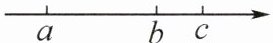
A.$|a|>|c|$
B.$a+c<0$
C.$abc<0$
D.$\frac{a}{b}= 1$
答案:
C
6. 若$a<1-\sqrt{7}<b$,且a,b是两个连续整数,则$a+b$的值是 (
A.-1
B.-2
C.-3
D.-4
C
)A.-1
B.-2
C.-3
D.-4
答案:
C 提示:因为$2<\sqrt{7}<3$,所以$-3<-\sqrt{7}<-2$,所以$-2<1-\sqrt{7}<-1$.因为a,b是两个连续整数,所以$a=-2$,$b=-1$,所以$a+b=-3$.
7. 绝对值小于$\sqrt{7}$的整数有
-2,-1,0,1,2
;这些整数之和是0
.
答案:
-2,-1,0,1,2 0
8. 化简:
(1)$|-2\sqrt{3}|=$
(2)$|\sqrt{3}-1.3|=$
(3)$(\sqrt{2}-1)^0=$
(1)$|-2\sqrt{3}|=$
$2\sqrt{3}$
;(2)$|\sqrt{3}-1.3|=$
$\sqrt{3}-1.3$
;(3)$(\sqrt{2}-1)^0=$
1
.
答案:
(1)$2\sqrt{3}$;
(2)$\sqrt{3}-1.3$;
(3)1
(1)$2\sqrt{3}$;
(2)$\sqrt{3}-1.3$;
(3)1
9. 比较大小:
(1)$-π$
(2)$-\sqrt{2}+1$
(3)$2\sqrt{3}$
(4)$\frac{\sqrt{5}-1}{2}$
(1)$-π$
<
$-3.14$;(2)$-\sqrt{2}+1$
>
$-\sqrt{3}+1$;(3)$2\sqrt{3}$
<
$3\sqrt{2}$;(4)$\frac{\sqrt{5}-1}{2}$
>
$\frac{1}{2}$.
答案:
(1)<;
(2)>;
(3)<;
(4)>
(1)<;
(2)>;
(3)<;
(4)>
10. 若$a= \sqrt[3]{7},b= \sqrt{5},c= 2$,则a,b,c的大小关系为
$a<c<b$
(用“<”连接).
答案:
$a<c<b$
11. 定义$[x]$为不大于x的最大整数.例如:$[2]= 2,[\sqrt{3}]= 1,[4.1]= 4$,则满足$[\sqrt{n}]= 5$的n的最大整数为
35
.
答案:
35 提示:根据题意,得$5\leqslant\sqrt{n}<6$,所以$25\leqslant n<36$,所以n的最大整数为35.
12. 请把下列各数填在相应的括号内:
$+4,0.333…,-|-\frac{1}{2}|,-(+\frac{2}{7}),π,-(-2),0,2.5,-1.232232223…$(相邻两个3之间依次多一个2).
正有理数:{
非负整数:{
负分数:{
无理数:{
$+4,0.333…,-|-\frac{1}{2}|,-(+\frac{2}{7}),π,-(-2),0,2.5,-1.232232223…$(相邻两个3之间依次多一个2).
正有理数:{
$+4,0.333\cdots,-(-2),2.5$
};非负整数:{
$+4,-(-2),0$
};负分数:{
$-\vert-\frac{1}{2}\vert,-(+\frac{2}{7})$
};无理数:{
$\pi,-1.232232223\cdots$(相邻两个3之间依次多一个2)
}.
答案:
正有理数:$\{+4,0.333\cdots,-(-2),2.5\}$;非负整数:$\{+4,-(-2),0\}$;负分数:$\{-\vert-\frac{1}{2}\vert,-(+\frac{2}{7})\}$;无理数:$\{\pi,-1.232232223\cdots$(相邻两个3之间依次多一个2)$\}$
13. 计算:
(1)$\sqrt{16}-\sqrt{(-5)^2}+\sqrt[3]{\frac{1}{8}}$;
(2)$|-2|+\sqrt{(-2)^2}+\sqrt[3]{-8}-(\frac{1}{3})^{-1}$.
(1)$\sqrt{16}-\sqrt{(-5)^2}+\sqrt[3]{\frac{1}{8}}$;
(2)$|-2|+\sqrt{(-2)^2}+\sqrt[3]{-8}-(\frac{1}{3})^{-1}$.
答案:
解:
(1)原式$=4-5+\frac{1}{2}=-\frac{1}{2}$;
(2)原式$=2+2+(-2)-3=-1$
(1)原式$=4-5+\frac{1}{2}=-\frac{1}{2}$;
(2)原式$=2+2+(-2)-3=-1$
查看更多完整答案,请扫码查看


