《2025年小题狂做八年级数学上册苏科版提优版》

1. 如图,两个正方形的面积分别为 64 和 49,则 AC 的长为(B)
A.15
B.17
C.23
D.113

答案： B

2. 已知一直角三角形的木板,三边的平方和为1800,则斜边的长为(C)
A.10
B.20
C.30
D.40

答案： C

3. 设a,b是直角三角形两条直角边的长.若该三角形的周长为6,斜边的长为2.5,则ab的值是(D)
A.1.5
B.2
C.2.5
D.3

答案： D

4. 如图,在等腰直角三角形 ACB 中,∠ACB= 90°,AC= BC,且$AB^2= 8,$以边AB,AC,BC 为直径画半圆,所得两个月形图案 AFCD 和 BGCE(图中阴影部分)的面积之和为(C)
A.8
B.4
C.2
D.1

答案： C 提示:由题意,易得AC=BC=2.所以阴影部分的面积之和为π$\left(\frac{AC}{2}\right)^2$+$S_{\triangle ACB}$-$\frac{1}{2}$π$\left(\frac{AB}{2}\right)^2$=π+2-π=2.

5. 如图,把由5个小正方形组成的十字形纸板剪开,以下剪法中能够将剪成的若干块拼成一个大正方形的有(填序号).

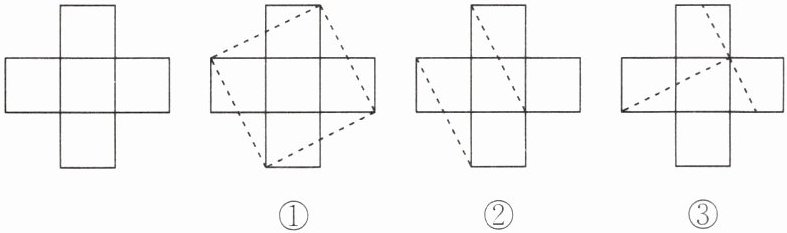
①③

答案： ①③

6. 如图,已知长方形 E 的长是宽的2倍,图中所有阴影四边形都是正方形,所有三角形都是直角三角形.若正方形 A,B,C 的面积依次为5,23,8,则正方形 D 的面积为1。

答案： 1 提示:设正方形A,B,C,D的边长分别为a,b,c,d,长方形E的长为m,宽为n.由题意可知,m=2n,$a^2$=5,$b^2$=23,$c^2$=8.由勾股定理,得$m^2$=$a^2$+$b^2$,$n^2$=$c^2$-$d^2$.因为m=2n,所以$m^2$=4$n^2$,所以$a^2$+$b^2$=4($c^2$-$d^2$),即5+23=4(8-$d^2$),解得$d^2$=1.所以正方形D的面积为1.

7. (2025 南京市建邺区期末)青朱出入图是魏晋时期数学家刘徽根据“割补术”运用数形关系证明勾股定理的几何证明法.如图,四边形 ABCD,DEFG,CGHI 均为正方形.若正方形 ABCD,CCHI 的面积分别为$S_1,S_2,$则 AF=$\sqrt{S_1-S_2}-\sqrt{S_2}$(用含$S_1$和$S_2$的代数式表示).

答案： $\sqrt{S_1-S_2}$-$\sqrt{S_2}$ 提示:由题意,得EF=DG=$\sqrt{DC^2-CG^2}$=$\sqrt{S_1-S_2}$.由割补,可知AE=IC=$\sqrt{S_2}$,所以AF=EF-AE=$\sqrt{S_1-S_2}$-$\sqrt{S_2}$.

8. 如图,在△ABD 中,AC⊥BD 于点 C,E 为AC 上一点,连接 BE,DE,DE 的延长线交AB 于点 F.已知 DE= AB,∠CAD= 45°.
(1)求证:△ABC≌△DEC.
证明:因为AC⊥BD,所以∠ACB=∠ACD=90°.因为∠CAD=45°,所以∠ADC=90°-∠CAD=45°=∠CAD,所以AC=DC.又因为AB=DE,所以Rt△ABC≌Rt△DEC(HL).
(2)DF⊥AB.(填位置关系,这个结论可以直接用于证明过程)
(3)利用图中阴影部分面积完成勾股定理的证明.
已知:如图,在△ABC 中,∠ACB= 90°,BC= a,AC= b,AB= c.
求证$:a^2+b^2= c^2.$
证明:因为△ABC≌△DEC,所以DE=AB=c,DC=AC=b,EC=BC=a.由题图,得$S_{阴影}$=$S_{\triangle BCE}$+$S_{\triangle ACD}$=$S_{\triangle ABD}$-$S_{\triangle ABE}$,所以$\frac{1}{2}$BC·EC+$\frac{1}{2}$AC·DC=$\frac{1}{2}$AB·DF-$\frac{1}{2}$AB·EF=$\frac{1}{2}$AB·(DF-EF)=$\frac{1}{2}$AB·DE,即$\frac{1}{2}a^2$+$\frac{1}{2}b^2$=$\frac{1}{2}c^2$,所以$a^2$+$b^2$=$c^2$.

答案： （1）证明:因为AC⊥BD,所以∠ACB=∠ACD=90°.因为∠CAD=45°,所以∠ADC=90°-∠CAD=45°=∠CAD,所以AC=DC.又因为AB=DE,所以Rt△ABC≌Rt△DEC(HL).（2）⊥（3）证明:因为△ABC≌△DEC,所以DE=AB=c,DC=AC=b,EC=BC=a.由题图,得$S_{阴影}$=$S_{\triangle BCE}$+$S_{\triangle ACD}$=$S_{\triangle ABD}$-$S_{\triangle ABE}$,所以$\frac{1}{2}$BC·EC+$\frac{1}{2}$AC·DC=$\frac{1}{2}$AB·DF-$\frac{1}{2}$AB·EF=$\frac{1}{2}$AB·(DF-EF)=$\frac{1}{2}$AB·DE,即$\frac{1}{2}a^2$+$\frac{1}{2}b^2$=$\frac{1}{2}c^2$,所以$a^2$+$b^2$=$c^2$.