《2025年小题狂做八年级数学上册苏科版提优版》

1. (2024 连云港市赣榆区期中)如图,∠MON= 90°,以点 O 为圆心,任意长为半径画弧,分别交 OM,ON 于点 A,D,再以点 A 为圆心,AO 长为半径画弧,与弧 AD 交于点 B,连接 OB,AB,AB 的延长线交 ON 于点 C. 若 OD= 4,则 CB 的长为 (B)

A.3
B.4
C.5
D.6
]

答案： B 提示:由作图可知,OA=OB=OD=4,OA=AB,所以△ABO为等边三角形,所以∠OAC=∠ABO=∠AOB=60°.因为∠MON=90°,所以∠BCO=∠BOC=30°,所以CB=OB=4.

2. 如图,在边长为 2 的等边三角形 ABC 中,点 D 在边 BC 上运动(不与点 B,C 重合),点 E 在边 AB 的延长线上,点 F 在边 AC 的延长线上,AD= DE= DF. 点 D 在边 BC 上从点 B 至点 C 的运动过程中,△BED 周长的变化规律为 (D)

A.不变
B.一直变小
C.先变大后变小
D.先变小后变大
]

答案： D 提示:因为AD=DE=DF,所以∠DAB=∠DEB,∠DAC=∠DFC.因为∠DAB+∠DAC=∠BAC=60°,所以∠DEB+∠DFC=60°.因为∠ABC=∠DEB+∠EDB=60°,所以∠EDB=∠DFC.因为∠ACB=∠DFC+∠FDC=60°,所以∠FDC=∠DEB,所以△BDE≌△CFD(AAS),所以BD=CF,BE=CD,所以△BED的周长为BD+BE+DE=BD+CD+AD=BC+AD.因为点D在边BC上从点B至点C的运动过程中,AD的长先变小后变大,所以△BED的周长先变小后变大.

3. 如图,∠AOB= 120°,OP 平分∠AOB,且 OP= 1. 若点 M,N 分别在 OA,OB 上,且△PMN 为等边三角形,则满足上述条件的△PMN 有 ( )

A.1 个
B.2 个
C.3 个
D.无数个
]

答案：
D 提示:如图,过点P作PM⊥OA于点M,PN⊥OB于点N.因为OP平分∠AOB,PM⊥OA,PN⊥OB,所以PM=PN,∠PMO=90°,∠PNO=90°.所以∠MPN=360°-∠AOB-∠PMO-∠PNO=60°.所以此时△PMN是等边三角形.当点M向MO方向移动时,使点N向NB方向移动,且∠MPM₁=∠NPN₁.则∠M₁PN₁=∠M₁PN+∠NPN₁=∠M₁PN+∠MPM₁=∠MPN=60°.易证△PMM₁≌△PNN₁(ASA).所以PM₁=PN₁.所以△M₁PN₁是等边三角形.所以当点M向MO方向移动,点N向NB方向移动,且∠MPM₁=∠NPN₁时,△M₁PN₁是等边三角形.同理可得,当点M向MA方向移动,点N向NO方向移动,且∠MPM₂=∠NPN₂时,△M₂PN₂是等边三角形.故满足条件的△PMN有无数个.

4. 如图是两块完全一样的含 30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点 M 转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点 C. 已知 AC= 5,则这两块直角三角板顶点 A,A'之间的距离为 ______2.5
]

答案： 2.5 提示:连接AA'.因为M是线段AC,A'C'的中点,AC=5,所以AM=MC=A'M=MC'=2.5.因为∠MA'C=30°,所以∠MCA'=∠MA'C=30°,所以∠AMA'=∠MCA'+∠MA'C=60°,所以△AA'M是等边三角形,所以AA'=AM=2.5.

5. 如图,在锐角三角形 ABC 中,∠A= 30°,BC= 3,S△ABC= 8,P 是边 BC 上的一动点,点 P 关于直线 AB,AC 的对称点分别是 M,N,连接 MN,则 MN 的最小值为 ______$\frac{16}{3}$.

答案： $\frac{16}{3}$ 提示:连接PM,PN,AM,AN,AP.因为点P关于直线AB,AC的对称点分别是M,N,所以AB垂直平分PM,AC垂直平分PN,所以AM=AP,AN=AP,∠MAB=∠PAB,∠NAC=∠PAC.因为∠PAB+∠PAC=30°,所以∠MAB+∠NAC=30°,所以∠MAN=60°,所以△AMN是等边三角形,所以MN=AM=AP.当AP⊥CB时,AP的长最小,此时MN的长最小.此时,由$S_{\triangle ABC}=8$,得$\frac{1}{2}BC\cdot AP=8$,解得AP=$\frac{16}{3}$,所以MN的最小值是$\frac{16}{3}$.

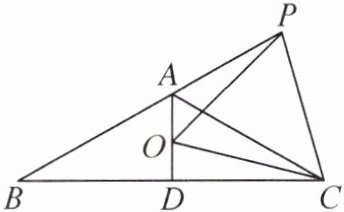
6. 如图,在等腰三角形 ABC 中,AB= AC,∠BAC= 120°,AD⊥BC 于点 D,P 是 BA 延长线上的一点,O 是线段 AD 上一点,OP= OC.
(1)求∠APO+∠DCO 的度数.
(2)求证:点 P 在 OC 的垂直平分线上.

答案： （1）解:连接OB.因为AB=AC,AD⊥BC,所以BD=CD,∠BAD=$\frac{1}{2}$∠BAC=60°,所以OB=OC,∠ABC=90°-∠BAD=30°.因为OP=OC,所以OB=OC=OP,所以∠APO=∠ABO,∠DCO=∠DBO,所以∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°. （2）证明:因为∠APC+∠DCP+∠ABC=180°,所以∠APC+∠DCP=150°.因为∠APO+∠DCO=30°,所以∠OPC+∠OCP=120°,所以∠POC=180°-（∠OPC+∠OCP）=60°.因为OP=OC,所以△OPC是等边三角形,所以OP=PC,所以点P在OC的垂直平分线上.