第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 在Rt△ABC中,∠C= 90°,周长为60,斜边长与一条直角边长之比为13:5,则Rt△ABC的斜边长为(
A.5
B.10
C.13
D.26
D
)A.5
B.10
C.13
D.26
答案:
D
2. 已知直角三角形的面积为15,两条直角边的和为11,则其斜边长的平方为(
A.61
B.62
C.63
D.64
A
)A.61
B.62
C.63
D.64
答案:
A
3. 如图,在Rt△ABC中,AB= 6,BC= 8,AD为∠BAC的平分线,将△ADC沿直线AD翻折得到△ADE,则DE的长为(
A.4
B.5
C.6
D.7
B
)A.4
B.5
C.6
D.7
答案:
B 提示:在Rt△ABC中,由勾股定理,得AC=10.由折叠,得AE=AC=10,所以BE=4.设DE=x,则BD=BC - DC=BC - DE=8 - x.在Rt△BDE中,由勾股定理,得(8 - x)²+4²=x²,解得x=5.所以DE的长为5.
4. 已知在△ABC中,AB= 17,AC= 10,边BC上的高AD= 8,则边BC的长为
21或9
.
答案:
21或9 提示:当高AD在△ABC内部时,BC=21;当高AD在△ABC的外部时,BC=9.
5. 如图,在△ABC中,AB= AC= 5,BC= 6,M为BC的中点,MN⊥AC于点N,则MN的长是
$\frac{12}{5}$
.
答案:
$\frac{12}{5}$ 提示:连接AM.因为AB=AC=5,M为BC的中点,所以AM⊥CM,$BM=CM=\frac{1}{2}BC=3$.在Rt△ABM中,根据勾股定理,得$AM=\sqrt{AB^2 - BM^2}=4$.又因为$S_{\triangle AMC}=\frac{1}{2}MN\cdot AC=\frac{1}{2}AM\cdot CM$,所以$MN=\frac{AM\cdot CM}{AC}=\frac{12}{5}$.
6. 如图,正方形网格中的每个小正方形的边长都是1,任意连接这些小正方形的顶点,可得到一些线段.请在图中画出AB= √2,AC= √5,AD= √13这样的线段.
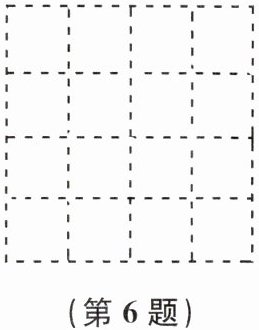

答案:
解:如图所示(答案不唯一).
解:如图所示(答案不唯一).

7. 如图,A是数轴上表示实数a的点.
(1)请用直尺和圆规在数轴上作出表示实数√2的点P.(保留作图痕迹,不写作法)
(2)利用数轴比较√2和a的大小,并说明理由.

(1)请用直尺和圆规在数轴上作出表示实数√2的点P.(保留作图痕迹,不写作法)
(2)利用数轴比较√2和a的大小,并说明理由.

答案:
解$:$
$(1)$如图$,$点$P$即为所求$.$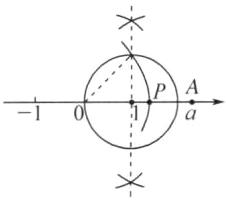
$(2)a>\sqrt{2}.$理由如下$:$在数轴上$,$位于右侧的数大于位于左侧的数$,$所以由$(1)$中所作的图$,$可知$a>\sqrt{2}. $
解$:$
$(1)$如图$,$点$P$即为所求$.$

$(2)a>\sqrt{2}.$理由如下$:$在数轴上$,$位于右侧的数大于位于左侧的数$,$所以由$(1)$中所作的图$,$可知$a>\sqrt{2}. $
8. 如图,△ACB和△DCE均是等腰直角三角形,∠ACB= ∠ECD= 90°,D为边AB上一点.
(1)求证:△ACE≌△BCD.
(2)若AD= 5,BD= 12,求DE的长.
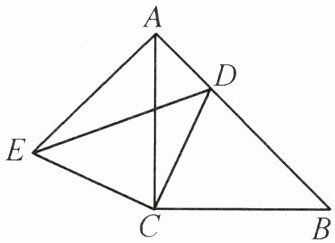
(1)求证:△ACE≌△BCD.
(2)若AD= 5,BD= 12,求DE的长.

答案:
(1)证明:因为△ACB和△DCE均是等腰直角三角形,$\angle ACB = \angle ECD = 90^{\circ}$,所以AC = BC,EC = DC,所以$\angle DCB = \angle ACB - \angle ACD = \angle ECD - \angle ACD = \angle ECA$.在△ACE和△BCD中,$\begin{cases}AC = BC\\\angle ECA = \angle DCB\\EC = DC\end{cases}$,所以△ACE≌△BCD(SAS).
(2)解:由
(1)知△ACE≌△BCD,所以AE = BD = 12,$\angle EAC = \angle DBC$.因为△ACB是等腰直角三角形,所以$\angle EAC = \angle DBC = \angle CAB = 45^{\circ}$,所以$\angle EAD = 90^{\circ}$.在Rt△ADE中,根据勾股定理,得$AD^2 + AE^2 = DE^2$,即$5^2 + 12^2 = DE^2$,所以DE = 13.
(1)证明:因为△ACB和△DCE均是等腰直角三角形,$\angle ACB = \angle ECD = 90^{\circ}$,所以AC = BC,EC = DC,所以$\angle DCB = \angle ACB - \angle ACD = \angle ECD - \angle ACD = \angle ECA$.在△ACE和△BCD中,$\begin{cases}AC = BC\\\angle ECA = \angle DCB\\EC = DC\end{cases}$,所以△ACE≌△BCD(SAS).
(2)解:由
(1)知△ACE≌△BCD,所以AE = BD = 12,$\angle EAC = \angle DBC$.因为△ACB是等腰直角三角形,所以$\angle EAC = \angle DBC = \angle CAB = 45^{\circ}$,所以$\angle EAD = 90^{\circ}$.在Rt△ADE中,根据勾股定理,得$AD^2 + AE^2 = DE^2$,即$5^2 + 12^2 = DE^2$,所以DE = 13.
9. 如图,在△ABC中,AB= AC,AD⊥BC于点D,∠CBE= 45°,BE分别交AC,AD于点E,F,连接CF.
(1)判断△BCF的形状,并说明理由.
(2)若AF= BC,求证:$BF^2+EF^2= AE^2.$

(1)判断△BCF的形状,并说明理由.
(2)若AF= BC,求证:$BF^2+EF^2= AE^2.$

答案:
(1)△BCF为等腰直角三角形.理由如下:因为AB = AC,AD⊥BC,所以BD = CD,所以AD垂直平分BC,所以BF = CF,所以$\angle BCF = \angle CBF = 45^{\circ}$,所以$\angle CFB = 180^{\circ} - \angle BCF - \angle CBF = 90^{\circ}$,所以△BCF为等腰直角三角形.
(2)在线段BF上取一点H,使BH = FE,连接CH.因为△BCF为等腰直角三角形,AD⊥BC,易得$\angle AFE = \angle DFB = \angle DBF = 45^{\circ}$.在△CHB和△AEF中,$\begin{cases}BH = FE\\\angle CBH = \angle AFE\\BC = FA\end{cases}$,所以△CHB≌△AEF(SAS),所以AE = CH,$\angle AEF = \angle CHB$.因为$\angle AEF + \angle CEF = 180^{\circ}$,$\angle CHB + \angle CHE = 180^{\circ}$,所以$\angle CEF = \angle CHE$,所以CE = CH.因为$\angle CFB = 90^{\circ}$,即CF⊥EH,所以EF = FH.由
(1)可知CF = BF.在Rt△CFH中,由勾股定理,得$CF^2 + FH^2 = CH^2$,所以$BF^2 + EF^2 = AE^2$.
(1)△BCF为等腰直角三角形.理由如下:因为AB = AC,AD⊥BC,所以BD = CD,所以AD垂直平分BC,所以BF = CF,所以$\angle BCF = \angle CBF = 45^{\circ}$,所以$\angle CFB = 180^{\circ} - \angle BCF - \angle CBF = 90^{\circ}$,所以△BCF为等腰直角三角形.
(2)在线段BF上取一点H,使BH = FE,连接CH.因为△BCF为等腰直角三角形,AD⊥BC,易得$\angle AFE = \angle DFB = \angle DBF = 45^{\circ}$.在△CHB和△AEF中,$\begin{cases}BH = FE\\\angle CBH = \angle AFE\\BC = FA\end{cases}$,所以△CHB≌△AEF(SAS),所以AE = CH,$\angle AEF = \angle CHB$.因为$\angle AEF + \angle CEF = 180^{\circ}$,$\angle CHB + \angle CHE = 180^{\circ}$,所以$\angle CEF = \angle CHE$,所以CE = CH.因为$\angle CFB = 90^{\circ}$,即CF⊥EH,所以EF = FH.由
(1)可知CF = BF.在Rt△CFH中,由勾股定理,得$CF^2 + FH^2 = CH^2$,所以$BF^2 + EF^2 = AE^2$.
查看更多完整答案,请扫码查看


