第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 如图是本地区一种产品30天的销售情况图象,图1是产品日销售量 y(件)与时间t(天)之间的函数关系,图2是一件产品的销售利润 z(元)与时间t(天)之间的函数关系.已知日销售利润= 日销售量×一件产品的销售利润,则下列结论错误的是 (
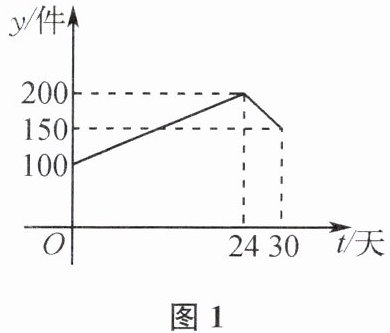

A.第24天的销售量为200件
B.第10天销售一件产品的利润是15元
C.第12天与第30天这两天的日销售利润相等
D.第30天的日销售利润是750元
C
)

A.第24天的销售量为200件
B.第10天销售一件产品的利润是15元
C.第12天与第30天这两天的日销售利润相等
D.第30天的日销售利润是750元
答案:
C 提示:由题图可知,$y=\left\{\begin{array}{l} \frac {25}{6}t+100(0≤t≤24),\\ -\frac {25}{3}t+400(24<t≤30),\end{array}\right. $$z=\left\{\begin{array}{l} -t+25(0≤t≤20),\\ 5(20<t≤30).\end{array}\right. $由题图1知,选项A正确;由题图2知,$z=-10+25=15$,故选项 B 正确;第12天的销售件数是$y=\frac {25}{6}×12+100=150$,一件产品的利润是$z=-12+25=13$,所以日销售利润是$150×13=1950(元)$,第30天的销售件数是150,一件产品的利润是5元,日销售利润是750元,故选项C错误,D正确.
2. 一天,小明从家出发匀速步行去学校上学.几分钟后,在家休假的爸爸发现小明忘带数学书,于是爸爸立即匀速跑步去追小明,爸爸追上小明后又以原速原路跑回家.小明拿到书后以原速的$\frac {5}{4}$快步赶往学校,并在从家出发23 min后到校(小明被爸爸追上时交流时间忽略不计).两人之间相距的路程 y(m)与小明从家出发到学校的步行时间 x(min)之间的函数关系如图所示,则小明家到学校的路程为______m.


2080
答案:
2080 提示:设小明原速度为x m/min,爸爸跑步速度为y m/min,则小明拿到书后的速度为1.25x m/min,家校距离为$11x+(23-11)×1.25x=26x m$.根据题意,得$\left\{\begin{array}{l} 11x=(16-11)y,\\ (16-11)×(1.25x+y)=1380,\end{array}\right. $解得$\left\{\begin{array}{l} x=80,\\ y=176.\end{array}\right. $所以小明家到学校的路程为$80×26=2080(m).$
3. 一列快车和一列慢车同时从甲地出发,分别以速度$v_{1},v_{2}$(单位:km/h,且$v_{1}>2v_{2}$)匀速驶向乙地,快车到达乙地后停留了2 h.沿原路仍以速度$v_{1}$匀速返回甲地.设慢车行驶的时间为x(h),两车之间的距离为y(km).图中的折线表示从慢车出发至慢车到达乙地的过程中,y与x之间的函数关系.
根据图象进行以下研究:
(1)甲、乙两地之间的距离为
(2)求线段AB,CD所表示的y与x之间的函数表达式.
(3)慢车出发多长时间后,两车相距480 km?
根据图象进行以下研究:
(1)甲、乙两地之间的距离为
900
km.(2)求线段AB,CD所表示的y与x之间的函数表达式.
由题图,可知慢车的速度为$\frac {900}{15}=60(km/h),$快车的速度为$\frac {900×2-10×60}{10-2}=150(km/h).$因为点 A 表示快车到达乙地,所以此时快车行驶的时间为$\frac {900}{150}=6(h),$两车距离为900-60×6=540(km),所以点A(6,540).设线段 AB 所表示的 y 与 x 之间的函数表达式为y_{1}=-60x+b.把点A(6,540)代入,得-60×6+b=540,解得b=900.所以线段 AB 所表示的 y 与 x 之间的函数表达式为y_{1}=-60x+900(6≤x≤8).因为两车的速度之和为60+150=210(km/h),所以设线段 CD 所表示的 y 与 x 之间的函数表达式为y_{2}=210x+n.把点C(10,0)代入,得210×10+n=0,解得n=-2100.因为快车到达乙地后停留了2 h,所以点 D 的横坐标为14,所以线段 CD 所表示的 y 与x 之间的函数表达式为y_{2}=210x-2100(10≤x≤14).
(3)慢车出发多长时间后,两车相距480 km?
当x=8时,y_{1}=-60×8+900=420.所以点B(8,420).由(2)知点A(6,540),因为420<480<540,所以分以下情况讨论:①线段 OA 所表示的 y 与 x 之间的函数表达式为y_{3}=90x(0≤x<6).令y_{3}=480,得$x=\frac {16}{3}.②$线段 AB 所表示的 y 与x 之间的函数表达式为y_{1}=-60x+900(6≤x≤8).令y_{1}=480,得x=7.③线段 CD 所表示的 y 与 x 之间的函数表达式为y_{2}=210x-2100(10≤x≤14).令y_{2}=480,得$x=\frac {86}{7}.$综上所述,慢车出发$\frac {16}{3}h$或7h或$\frac {86}{7}h$后,两车相距480 km.
答案:
(1)900
(2)由题图,可知慢车的速度为$\frac {900}{15}=60(km/h),$快车的速度为$\frac {900×2-10×60}{10-2}=150(km/h).$因为点 A 表示快车到达乙地,所以此时快车行驶的时间为$\frac {900}{150}=6(h),$两车距离为900-60×6=540(km),所以点A(6,540).设线段 AB 所表示的 y 与 x 之间的函数表达式为y_{1}=-60x+b.把点A(6,540)代入,得-60×6+b=540,解得b=900.所以线段 AB 所表示的 y 与 x 之间的函数表达式为y_{1}=-60x+900(6≤x≤8).因为两车的速度之和为60+150=210(km/h),所以设线段 CD 所表示的 y 与 x 之间的函数表达式为y_{2}=210x+n.把点C(10,0)代入,得210×10+n=0,解得n=-2100.因为快车到达乙地后停留了2 h,所以点 D 的横坐标为14,所以线段 CD 所表示的 y 与x 之间的函数表达式为y_{2}=210x-2100(10≤x≤14).
(3)当x=8时,y_{1}=-60×8+900=420.所以点B(8,420).由
(2)知点A(6,540),因为420<480<540,所以分以下情况讨论:①线段 OA 所表示的 y 与 x 之间的函数表达式为y_{3}=90x(0≤x<6).令y_{3}=480,得$x=\frac {16}{3}.②$线段 AB 所表示的 y 与x 之间的函数表达式为y_{1}=-60x+900(6≤x≤8).令y_{1}=480,得x=7.③线段 CD 所表示的 y 与 x 之间的函数表达式为y_{2}=210x-2100(10≤x≤14).令y_{2}=480,得$x=\frac {86}{7}.$综上所述,慢车出发$\frac {16}{3}h$或7h或$\frac {86}{7}h$后,两车相距480 km.
(1)900
(2)由题图,可知慢车的速度为$\frac {900}{15}=60(km/h),$快车的速度为$\frac {900×2-10×60}{10-2}=150(km/h).$因为点 A 表示快车到达乙地,所以此时快车行驶的时间为$\frac {900}{150}=6(h),$两车距离为900-60×6=540(km),所以点A(6,540).设线段 AB 所表示的 y 与 x 之间的函数表达式为y_{1}=-60x+b.把点A(6,540)代入,得-60×6+b=540,解得b=900.所以线段 AB 所表示的 y 与 x 之间的函数表达式为y_{1}=-60x+900(6≤x≤8).因为两车的速度之和为60+150=210(km/h),所以设线段 CD 所表示的 y 与 x 之间的函数表达式为y_{2}=210x+n.把点C(10,0)代入,得210×10+n=0,解得n=-2100.因为快车到达乙地后停留了2 h,所以点 D 的横坐标为14,所以线段 CD 所表示的 y 与x 之间的函数表达式为y_{2}=210x-2100(10≤x≤14).
(3)当x=8时,y_{1}=-60×8+900=420.所以点B(8,420).由
(2)知点A(6,540),因为420<480<540,所以分以下情况讨论:①线段 OA 所表示的 y 与 x 之间的函数表达式为y_{3}=90x(0≤x<6).令y_{3}=480,得$x=\frac {16}{3}.②$线段 AB 所表示的 y 与x 之间的函数表达式为y_{1}=-60x+900(6≤x≤8).令y_{1}=480,得x=7.③线段 CD 所表示的 y 与 x 之间的函数表达式为y_{2}=210x-2100(10≤x≤14).令y_{2}=480,得$x=\frac {86}{7}.$综上所述,慢车出发$\frac {16}{3}h$或7h或$\frac {86}{7}h$后,两车相距480 km.
查看更多完整答案,请扫码查看


