第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2所示的方式放置在最大的正方形内.若已知图中阴影部分的面积,则一定能求出(
A.直角三角形的面积
B.最大正方形的面积
C.较小的两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积之和
C
)A.直角三角形的面积
B.最大正方形的面积
C.较小的两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积之和
答案:
C 提示:设直角三角形的斜边长为c,较长直角边为b,较短直角边为a.由勾股定理,得$c^2 = a^2 + b^2$,阴影部分的面积为$c^2 - b^2 - a(c - b)=a^2 - ac + ab = a(a + b - c)$.由题图可知,较小两个正方形重叠部分的宽为$a - (c - b)$,长为a,则面积为$a(a + b - c)$.所以若已知题图中阴影部分的面积,则一定能求出较小两个正方形重叠部分的面积.
2. 如图,在△ABC中,∠ACB= 90°,BC= 3,AC= 4,D是AB的中点,将△ACD沿CD翻折得到△ECD,连接AE,BE,则线段BE的长为(
A.7/5
B.3/2
C.5/3
D.2
A
)A.7/5
B.3/2
C.5/3
D.2
答案:
A 提示:延长CD交AE于点H,过点C作CF⊥AB于点F.在Rt△ABC中,由勾股定理,得AB = 5.因为$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CF$,所以$\frac{1}{2}×3×4=\frac{1}{2}×5× CF$,所以$CF=\frac{12}{5}$.因为D为AB的中点,$\angle ACB = 90^{\circ}$,所以AD = BD = CD.由翻折的性质,可知AC = CE,所以CH⊥AE,所以AH = HE.易证Rt△CDF≌Rt△ADH(AAS),所以AH = CF,所以$AE = 2AH = 2CF=\frac{24}{5}$.由翻折的性质,可知DE = AD = DB,所以$\angle DAE = \angle DEA$,$\angle DBE = \angle DEB$.又因为$\angle DAE + \angle DBE + \angle DEA + \angle DEB = 180^{\circ}$,所以$\angle AEB = \angle DEA + \angle DEB = 90^{\circ}$,所以△ABE为直角三角形.所以$BE=\sqrt{AB^2 - AE^2}=\sqrt{5^2 - (\frac{24}{5})^2}=\frac{7}{5}$.
3. 如图,在Rt△ABC中,∠C= 90°,AC= 6,BC= 8,D,E分别是边AB和边CB上的点,把△BDE沿着直线DE折叠.若点B落在边AC上,则CE的取值范围是
$\frac{7}{4}\leqslant CE\leqslant4$
.
答案:
$\frac{7}{4}\leqslant CE\leqslant4$ 提示:设点B的对应点为F,CE = x,则BE = 8 - x.由题意,得EF = BE = 8 - x.设CF = m.在Rt△CEF中,由勾股定理,得$CF^2 = EF^2 - CE^2$,即$m^2=(8 - x)^2 - x^2 = 64 - 16x$.因为$0\leqslant m\leqslant6$,所以$0\leqslant64 - 16x\leqslant36$,解得$\frac{7}{4}\leqslant x\leqslant4$,即$\frac{7}{4}\leqslant CE\leqslant4$.(也可以通过观察图形,当点B落在点A时,CE取得最小值,此时由勾股定理可知,CE的长为$\frac{7}{4}$;当点B落在点C时,CE取得最大值4.)
4. 阅读与应用:下面是小敏写的数学日记的一部分,请你认真阅读,并完成相应的任务.
|无理数与线段长|
|今天我们借助勾股定理,在数轴上找到了一些特殊的无理数对应的点,认识了“数轴上的点与实数一一对应”这一事实.|
|回顾梳理:要在数轴上找到表示±√2的点,关键是在数轴上构造线段OA= OA'= √2.如图1,正方形的边长为1个单位长度,以原点O为圆心,对角线长为半径画弧与数轴分别交于点A,A',则点A对应的数为√2,点A'对应的数为-√2.类似地,我们可以在数轴上找到表示±√5,±√10,…的点.|
|拓展思考:如图2,改变图1中正方形的位置,用类似的方法作图,可在数轴上构造出线段OB与OB',其中O仍为原点,点B,B'分别在原点的右侧、左侧,可由线段OB与OB'的长得得到点B,B'所表示的无理数.按照这样的思路,只要构造出特定长度的线段,就能在数轴上找到无理数对应的点.|
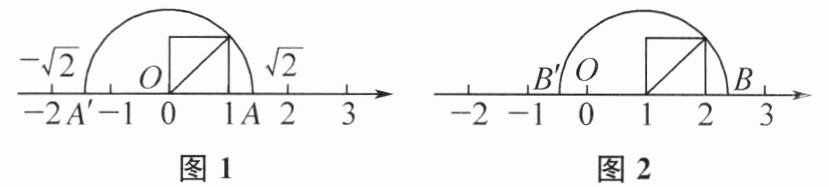
任务:
(1)“拓展思考”中,线段OB的长为______,OB'的长为______;点B表示的数为______,点B'表示的数为______.
(2)请在图3所示的数轴上,画图确定表示2-√10的点M.

|无理数与线段长|
|今天我们借助勾股定理,在数轴上找到了一些特殊的无理数对应的点,认识了“数轴上的点与实数一一对应”这一事实.|
|回顾梳理:要在数轴上找到表示±√2的点,关键是在数轴上构造线段OA= OA'= √2.如图1,正方形的边长为1个单位长度,以原点O为圆心,对角线长为半径画弧与数轴分别交于点A,A',则点A对应的数为√2,点A'对应的数为-√2.类似地,我们可以在数轴上找到表示±√5,±√10,…的点.|
|拓展思考:如图2,改变图1中正方形的位置,用类似的方法作图,可在数轴上构造出线段OB与OB',其中O仍为原点,点B,B'分别在原点的右侧、左侧,可由线段OB与OB'的长得得到点B,B'所表示的无理数.按照这样的思路,只要构造出特定长度的线段,就能在数轴上找到无理数对应的点.|

任务:
(1)“拓展思考”中,线段OB的长为______,OB'的长为______;点B表示的数为______,点B'表示的数为______.
(2)请在图3所示的数轴上,画图确定表示2-√10的点M.

答案:
(1)$\sqrt{2}+1$ $\sqrt{2}-1$ $\sqrt{2}+1$ $1-\sqrt{2}$
(2)因为$2 - \sqrt{10}<0$,所以点M在数轴的负半轴.如图,以表示的数为2的点为圆心,在圆心的左侧,作出以1个单位长度和3个单位长度为直角边的直角三角形,其斜边长为$\sqrt{3^2 + 1^2}=\sqrt{10}$,然后以$\sqrt{10}$为半径画弧,与数轴负半轴相交的点M即为所求.
(1)$\sqrt{2}+1$ $\sqrt{2}-1$ $\sqrt{2}+1$ $1-\sqrt{2}$
(2)因为$2 - \sqrt{10}<0$,所以点M在数轴的负半轴.如图,以表示的数为2的点为圆心,在圆心的左侧,作出以1个单位长度和3个单位长度为直角边的直角三角形,其斜边长为$\sqrt{3^2 + 1^2}=\sqrt{10}$,然后以$\sqrt{10}$为半径画弧,与数轴负半轴相交的点M即为所求.

查看更多完整答案,请扫码查看


