第72页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
1. 公式L= L₀+KP表示当重力为P的物体作用在弹簧上时弹簧的长度.L₀(cm)表示弹簧的初始长度,K(cm)表示单位重力物体作用在弹簧上时弹簧拉伸的长度.下面给出的四个公式中,表明这是一个短而硬的弹簧的是(
A.L= 10+0.5P
B.L= 10+5P
C.L= 80+0.5P
D.L= 80+5P
A
)A.L= 10+0.5P
B.L= 10+5P
C.L= 80+0.5P
D.L= 80+5P
答案:
A
2. 若一次函数y= kx+3的自变量取值增加2,函数值就相应减少2,则k的值为(
A.2
B.-2
C.-1
D.4
C
)A.2
B.-2
C.-1
D.4
答案:
C
3. 某商店今年6月初销售纯净水的数量如下表:
| 日期 | 1 | 2 | 3 | 4 |
| 数量/瓶 | 120 | 125 | 130 | 135 |
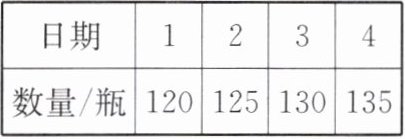
观察此表,利用所学的函数知识预测今年6月7日该商店销售纯净水的数量
| 日期 | 1 | 2 | 3 | 4 |
| 数量/瓶 | 120 | 125 | 130 | 135 |

观察此表,利用所学的函数知识预测今年6月7日该商店销售纯净水的数量
150
瓶.
答案:
150
4. 下表给出的是关于某个一次函数的自变量x及其对应的函数值y的若干信息.

| x | ... | -1 | 1 | 2 | ... |
| y | ... | m | 2 | n | ... |
请根据表格中的相关数据计算:m+2n= ______.

| x | ... | -1 | 1 | 2 | ... |
| y | ... | m | 2 | n | ... |
请根据表格中的相关数据计算:m+2n= ______.
6
答案:
6 提示:设这个一次函数的表达式为y=kx+b(k≠0),则-k+b=m①;k+b=2②;2k+b=n③.所以m+2n=①+2×③=3k+3b=3×2=6.
5. 已知$y= y_1+y_2,$且$y_1-3$与x成正比例$,y_2$与x-2成正比例.当x= 2时,y= 7;当x= 1时,y= 0.
(1) 求出y与x之间的函数表达式.
(2) 当x= 4时,求y的值.
(3) 当y= 6时,求x的值.
(1) 求出y与x之间的函数表达式.
(2) 当x= 4时,求y的值.
(3) 当y= 6时,求x的值.
答案:
解:
(1)设y₁-3=k₁x,y₂=k₂(x-2),则y=y₁+y₂=k₁x+3+k₂(x-2).把x=2,y=7和x=1,y=0代入,得{2k₁+3=7,k₁+3-k₂=0,解得{k₁=2,k₂=5,所以y=2x+3+5(x-2)=7x-7,所以y与x之间的函数表达式为y=7x-7.
(2)把x=4代入y=7x-7,得y=7×4-7=21.
(3)把y=6代入y=7x-7,得x=13/7.
(1)设y₁-3=k₁x,y₂=k₂(x-2),则y=y₁+y₂=k₁x+3+k₂(x-2).把x=2,y=7和x=1,y=0代入,得{2k₁+3=7,k₁+3-k₂=0,解得{k₁=2,k₂=5,所以y=2x+3+5(x-2)=7x-7,所以y与x之间的函数表达式为y=7x-7.
(2)把x=4代入y=7x-7,得y=7×4-7=21.
(3)把y=6代入y=7x-7,得x=13/7.
6. 某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1) 求每台A型电脑和B型电脑的销售利润.
(2) 该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数表达式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?最大利润是多少?
(1) 求每台A型电脑和B型电脑的销售利润.
(2) 该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
①求y关于x的函数表达式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?最大利润是多少?
答案:
解:
(1)设每台A型电脑销售利润为a元,每台B型电脑的销售利润为b元.根据题意,得{10a+20b=4000,20a+10b=3500,解得{a=100,b=150.答:每台A型电脑销售利润为100元,每台B型电脑的销售利润为150元.
(2)①根据题意,得y=100x+150(100-x),即y=-50x+15000.因为100-x≤2x,所以x≥33 1/3.所以y关于x的函数表达式为y=-50x+15000(x为整数,34≤x≤99).②因为y=-50x+15000,x的值越大,y的值越小.所以当x=34时,100-x=66,此时最大利润是y=-50×34+15000=13300.答:商店购进34台A型电脑和66台B型电脑时,销售利润最大,最大利润是13300元.
(1)设每台A型电脑销售利润为a元,每台B型电脑的销售利润为b元.根据题意,得{10a+20b=4000,20a+10b=3500,解得{a=100,b=150.答:每台A型电脑销售利润为100元,每台B型电脑的销售利润为150元.
(2)①根据题意,得y=100x+150(100-x),即y=-50x+15000.因为100-x≤2x,所以x≥33 1/3.所以y关于x的函数表达式为y=-50x+15000(x为整数,34≤x≤99).②因为y=-50x+15000,x的值越大,y的值越小.所以当x=34时,100-x=66,此时最大利润是y=-50×34+15000=13300.答:商店购进34台A型电脑和66台B型电脑时,销售利润最大,最大利润是13300元.
查看更多完整答案,请扫码查看


