《2025年小题狂做八年级数学上册苏科版提优版》

1. 直角三角形的两边分别是3,5,那么这个三角形的面积是(D)
A.6
B.12 或 7.5
C.7.5
D.6 或 7.5

答案： D

2. 如图,在数轴上点 A 表示的数为 2,在点 A 的右侧作一个长为 2,宽为 1 的长方形 ABCD,将对角线 AC 绕点 A 逆时针旋转,使对角线的另一端落在数轴上的点 E 处,则点 E 表示的数是(C)
A.$\sqrt {5}$
B.$-\sqrt {5}$
C.$2-\sqrt {5}$
D.$\sqrt {5}-2$

答案： C 提示:由题意可知,AB=1,BC=2.根据勾股定理,得AC=√(AB²+BC²)=√5,所以AC=AE=√5.所以点E表示的数是2-√5.

3. 如图,网格中小正方形的边长都是 1,四边形 ABCD 的四个顶点都在格点上,在四条边 AB,BC,CD,AD 中,长度是无理数的条数为(B)
A.1
B.2
C.3
D.4

答案： B

4. 为了比较$\sqrt {5}+1与\sqrt {10}$的大小,可以构造如图所示的图形进行推算,其中$∠C= 90^{\circ },BC= 3$,点 D 在边 BC 上,且$BD= AC= 1$.通过计算,可得$\sqrt {5}+1$＞$\sqrt {10}$(填“＞”“＜”或“=”).

答案： ＞ 提示:因为∠C=90°,BD=AC=1,BC=3,所以CD=BC - BD=2.由勾股定理,得AB=√10,AD=√5.因为AD + BD＞AB,所以√5 + 1＞√10.

5. 如图,AB,BC,CD,DE 是四根长度均为 5 cm 的小木棒,点 A,C,E 共线. 若$AC= 6cm,CD⊥BC$,则线段 CE 的长是______.

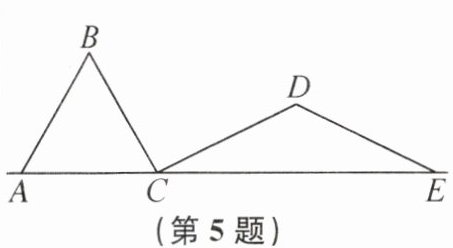
答案： 8cm 提示:过点B作BM⊥AC于点M,过点D作DN⊥CE于点N,则∠BMC=∠CND=90°,AM=CM=1/2AC=3cm,CN=EN.在Rt△BCM中,由勾股定理,得BM=√(BC² - CM²)=4cm.因为CD⊥BC,所以∠BCD=90°.所以∠BCM + ∠CBM=90°=∠BCM + ∠DCN,所以∠CBM=∠DCN.易证△BCM≌△CDN,所以CN=BM=4cm,所以CE=2CN=8cm.

6. 如图,把长为 12 cm 的长方形纸条 ABCD 沿 EF,GH 所在的直线同时翻折,B,C 两点恰好落在边 AD 上的点 P 处,且$∠FPH= 90^{\circ },BF= 3cm$,则 FH 的长为5cm.

答案： 5 提示:由翻折的性质,得PF=BF=3cm,CH=PH.设FH=xcm,则PH=CH=(9 - x)cm.在Rt△PFH中,由勾股定理,得FH²=PH²+PF²,即x²=(9 - x)²+3²,解得x=5.

7. (2025 南京市鼓楼区期末)用两种方法证明“垂线段最短”. 如图 1,点 P 在直线 l 外,$PA⊥l$,垂足为 A,Q 为直线 l 上不同于点 A 的任意一点. 求证:$PA＜PQ.$
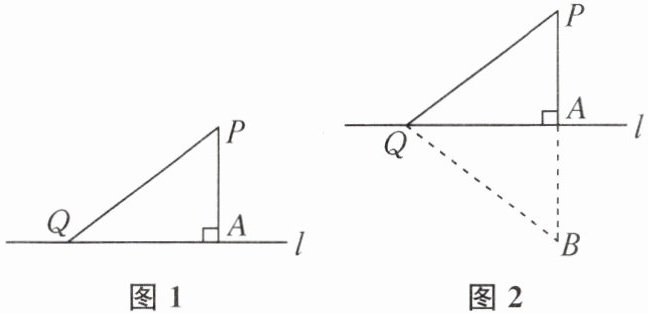
(1)小明的操作是:如图 2,延长 PA 至点 B,使得$AB= PA$,连接 BQ,……请根据小明的操作完成证明.
(2)小芳发现还可以通过“勾股定理”来证明,请根据小芳的想法完成证明.

答案： 证明:
(1)延长PA至点B,使得AB=PA,连接BQ,则PB=2PA.又因为QA⊥PB,所以QA垂直平分PB,所以PQ=BQ.因为PQ + BQ＞PB,所以2PQ＞2PA,所以PA＜PQ.
(2)因为PA⊥l,所以∠PAQ=90°,所以PQ²=PA²+AQ²,所以PA²＜PQ²,所以PA＜PQ.