第98页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
11 [2024沈阳126中月考]下列投影一定不会改变△ABC的形状和大小的是 (
A. 中心投影
B. 平行投影
C. 当△ABC平行于投影面时的正投影
D. 当△ABC平行于投影面时的中心投影
C
)A. 中心投影
B. 平行投影
C. 当△ABC平行于投影面时的正投影
D. 当△ABC平行于投影面时的中心投影
答案:
C
12 教材P132T1变式 [2024阜新期末]下图是一天中四个不同时刻两座建筑物的影子,将它们按时间先后顺序排列正确的是 (
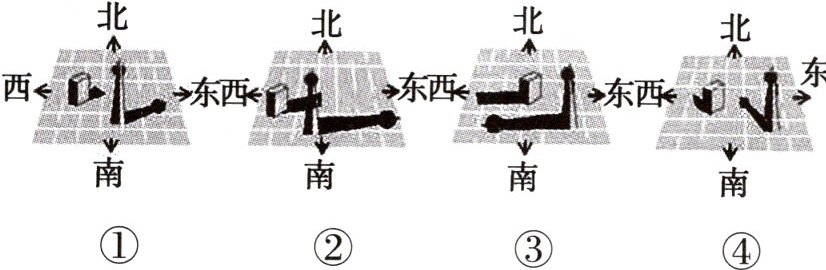
A. ③①④②
B. ③②①④
C. ③④①②
D. ②④①③
C
)
A. ③①④②
B. ③②①④
C. ③④①②
D. ②④①③
答案:
C 由于太阳从东边升起,西边落下,所以物体影子的方向为正西—西北—正北—东北—正东,所以影子的变化顺序为③④①②.
策略点拨
太阳光下物体影子的变化规律
在太阳光下,物体的投影随时间的变化而变化,体现在长度和偏移方向两个方面:由早上到傍晚,影子长度变化为长—短—长,中午是分界点;偏移方向变化为西—北偏西—北—北偏东—东(北半球).
策略点拨
太阳光下物体影子的变化规律
在太阳光下,物体的投影随时间的变化而变化,体现在长度和偏移方向两个方面:由早上到傍晚,影子长度变化为长—短—长,中午是分界点;偏移方向变化为西—北偏西—北—北偏东—东(北半球).
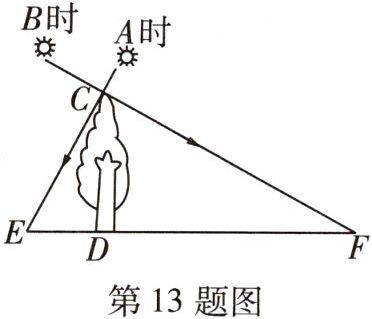
13 [2025阳泉期中]如图,在A时测得某树的影长DE为4m,B时又测得该树的影长DF为16m,若两次日照的光线互相垂直,则树的高度CD为
8
m.
答案:
8 由题意知∠EDC=∠CDF=∠ECF=90°,
∴∠E+∠ECD=∠ECD+∠DCF=90°,
∴∠E=∠DCF,
∴△EDC∽△CDF,
∴$\frac{ED}{CD}=\frac{CD}{FD}$,即$CD^{2}=ED\cdot FD$,
∴$CD^{2}=4×16=64$,
∴CD=8m.
∴∠E+∠ECD=∠ECD+∠DCF=90°,
∴∠E=∠DCF,
∴△EDC∽△CDF,
∴$\frac{ED}{CD}=\frac{CD}{FD}$,即$CD^{2}=ED\cdot FD$,
∴$CD^{2}=4×16=64$,
∴CD=8m.
14 某地夏季中午,当太阳移到屋顶上方偏南时,光线与地面成60°角,房屋向南的窗户AB= 1.6m.现要在窗户外面的上方安装一个水平遮阳篷AC(如图所示).要使此时的太阳光线不能直接射入室内,遮阳篷AC的宽度至少为
$\frac{8\sqrt{3}}{15}$
m.
答案:
$\frac{8\sqrt{3}}{15}$ 连接AB,此时△ABC为直角三角形,且∠ABC=30°,∠BAC=90°,所以BC=2AC.在Rt△ABC中,由勾股定理,得$AB^{2}+AC^{2}=BC^{2}$,即$1.6^{2}+AC^{2}=(2AC)^{2}$,所以$AC=\frac{8\sqrt{3}}{15}$m.所以遮阳篷AC的宽度至少为$\frac{8\sqrt{3}}{15}$m.
15 [2024烟台期末]如图,正方形纸板ABCD在投影面α上的正投影为四边形$A_1B_1C_1D_1,$其中边AB,CD与投影面α平行,AD,BC与投影面α不平行.若正方形ABCD的边长为$5cm,∠BCC_1= 45°,$求其投影$A_1B_1C_1D_1$的面积.
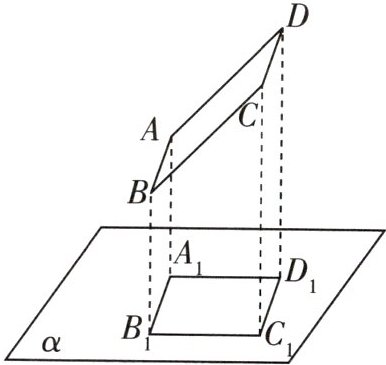

答案:
解:如图,过点B作BH⊥CC₁于点H,
∵∠BCC₁=45°,BC=5cm,
∴$BH=\frac{5\sqrt{2}}{2}$cm.
∵正方形纸板ABCD在投影面α上的正投影为四边形A₁B₁C₁D₁,边AB,CD与投影面α平行,
∴四边形A₁B₁C₁D₁为矩形,且$B_{1}C_{1}=BH=\frac{5\sqrt{2}}{2}$cm,$C_{1}D_{1}=CD=5$cm,
∴四边形A₁B₁C₁D₁的面积为$\frac{5\sqrt{2}}{2}×5=\frac{25\sqrt{2}}{2}$(cm²).

解:如图,过点B作BH⊥CC₁于点H,
∵∠BCC₁=45°,BC=5cm,
∴$BH=\frac{5\sqrt{2}}{2}$cm.
∵正方形纸板ABCD在投影面α上的正投影为四边形A₁B₁C₁D₁,边AB,CD与投影面α平行,
∴四边形A₁B₁C₁D₁为矩形,且$B_{1}C_{1}=BH=\frac{5\sqrt{2}}{2}$cm,$C_{1}D_{1}=CD=5$cm,
∴四边形A₁B₁C₁D₁的面积为$\frac{5\sqrt{2}}{2}×5=\frac{25\sqrt{2}}{2}$(cm²).

16 模型观念 [2025枣庄四十一中月考]甲、乙两栋楼的位置如图1,图2所示,甲楼AB高16米.
(1)如图1,当地中午12时,物高与影长的比是1:√2,甲楼的影子刚好不落到乙楼上,则两楼间距BD的长为______米.
(2)当地下午14时,物高与影长的比是1:2.如图2,甲楼的影子有一部分落在乙楼上,求落在乙楼上的影子DE的长.
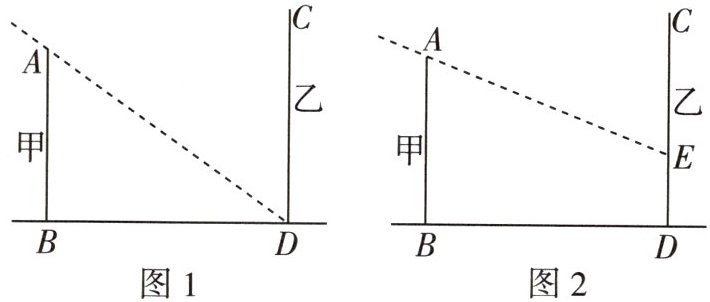
(1)如图1,当地中午12时,物高与影长的比是1:√2,甲楼的影子刚好不落到乙楼上,则两楼间距BD的长为______米.
(2)当地下午14时,物高与影长的比是1:2.如图2,甲楼的影子有一部分落在乙楼上,求落在乙楼上的影子DE的长.

答案:
解:
(1)$16\sqrt{2}$
由题意,得$\frac{AB}{BD}=\frac{1}{\sqrt{2}}$,即$\frac{16}{BD}=\frac{1}{\sqrt{2}}$,解得$BD=16\sqrt{2}$(米).
(2)如图,设FE⊥AB于点F,那么在Rt△AEF中,∠AFE=90°,EF=BD=$16\sqrt{2}$米.

∵物高与影长的比是1:2,
∴$\frac{AF}{EF}=\frac{1}{2}$,
∴$AF=\frac{1}{2}EF=8\sqrt{2}$(米),
∴DE=FB=AB - AF=$(16 - 8\sqrt{2})$米.
答:落在乙楼上的影子DE的长为$(16 - 8\sqrt{2})$米.
解:
(1)$16\sqrt{2}$
由题意,得$\frac{AB}{BD}=\frac{1}{\sqrt{2}}$,即$\frac{16}{BD}=\frac{1}{\sqrt{2}}$,解得$BD=16\sqrt{2}$(米).
(2)如图,设FE⊥AB于点F,那么在Rt△AEF中,∠AFE=90°,EF=BD=$16\sqrt{2}$米.

∵物高与影长的比是1:2,
∴$\frac{AF}{EF}=\frac{1}{2}$,
∴$AF=\frac{1}{2}EF=8\sqrt{2}$(米),
∴DE=FB=AB - AF=$(16 - 8\sqrt{2})$米.
答:落在乙楼上的影子DE的长为$(16 - 8\sqrt{2})$米.
查看更多完整答案,请扫码查看


