《2025年一遍过九年级初中数学上册北师大版》

1 [2024上海静安区一模]下列选项中的两个图形一定相似的是 (B)

A. 两个平行四边形
B. 两个正方形
C. 两个菱形
D. 两个等腰三角形

答案： B

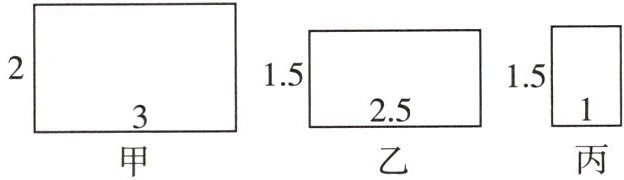
2 [2024唐山路南区期末]如图所示的三个矩形,其中是相似图形的是 (B)

A. 甲和乙
B. 甲和丙
C. 乙和丙
D. 甲、乙和丙

答案： B 根据题意得，矩形甲的长与宽的比是 $3:2$，矩形乙的长与宽的比是 $5:3$，矩形丙的长与宽的比是 $3:2$，矩形的四个角都是直角，所以矩形甲和矩形丙相似。
名师点睛
观察题目中所给图形，找出形状相同的图形。边数相同并不代表形状相同，判断两个图形是否相似一定要抓住“形状相同”这一本质特征。有时不仅要从“形”去观察，还应从“量”的角度去推断。

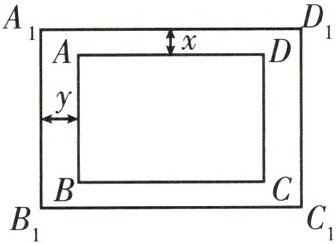
3 教材P88随堂练习T2变式 如图,在矩形花坛ABCD四周修筑小路,已知AB= 20m,AD= 30m.如果相对着的两条小路的宽均相等,宽度分别为x,y,试问小路的宽x与y的比值为多少时,能使得小路四周所围成的矩形$A_1B_1C_1D_1$和矩形ABCD相似.

$\frac{2}{3}$

答案： 解：当 $\frac{20 + 2x}{20} = \frac{30 + 2y}{30}$，即 $\frac{x}{y} = \frac{2}{3}$ 时，小路四周所围成的矩形 $A_1B_1C_1D_1$ 和矩形 $ABCD$ 相似，
∴ 当小路的宽 $x$ 与 $y$ 的比值为 $\frac{2}{3}$ 时，能使小路四周所围成的矩形 $A_1B_1C_1D_1$ 和矩形 $ABCD$ 相似。

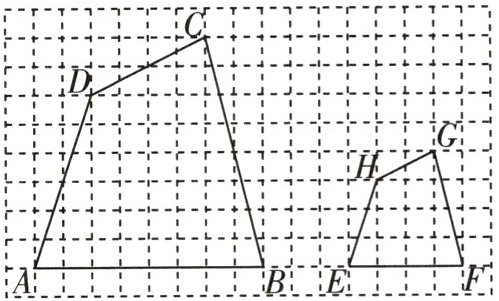
4 [2025佛山禅城区月考]如图,设小正方形的边长为1,四边形ABCD与四边形EFGH相似,且它们的顶点都在格点上,则它们的相似比是 (2:1)
A. $\sqrt{5}:1$
B. $\sqrt{5}:2$
C. $2:1$
D. $3:1$

答案： C
∵ 四边形 $ABCD \backsim$ 四边形 $EFGH$，
∴ $\frac{AB}{EF} = \frac{8}{4} = 2$，
∴ 它们的相似比是 $2:1$。

5 [2024淮南谢家集区期末]一个多边形的边长分别为2,3,4,5,6,另一个与它相似的多边形的最长边长为24,则这个多边形的最短边长为 (B)
A. 6
B. 8
C. 10
D. 12

答案： B 设这个多边形的最短边长为 $x$，
∵ 这两个多边形相似，
∴ $\frac{24}{6} = \frac{x}{2}$，
∴ $x = 8$。

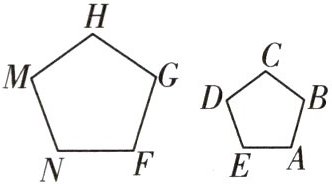
6 如图,正五边形FGHMN∽正五边形ABCDE,若AB:FG= 2:3,则下列结论正确的是 (B)

A. $2DE= 3MN$
B. $3DE= 2MN$
C. $3\angle A= 2\angle F$
D. $2\angle A= 3\angle F$

答案： B 因为相似多边形的对应角相等，对应边成比例，所以 $\angle A = \angle F$，$DE:MN = 2:3$，所以 $3DE = 2MN$。

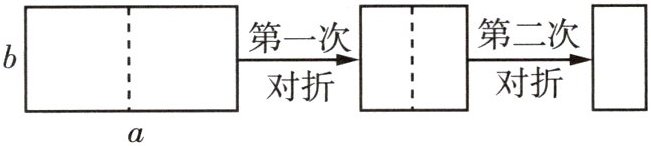
7 [2025深圳翠园文锦中学段考]如图,取一张长为a,宽为b的矩形纸片,将它对折两次后得到一张小矩形纸片,若要使小矩形纸片与原矩形纸片相似,则$a:b=$$2:1$.

答案： $2:1$ 对折两次后得到的小矩形纸片的长为 $b$，宽为 $\frac{1}{4}a$，
∵ 小矩形纸片与原矩形纸片相似，
∴ $\frac{a}{b} = \frac{b}{\frac{1}{4}a}$，又
∵ $a ＞ 0$，$b ＞ 0$，
∴ $\frac{a}{b} = 2$，即 $a:b = 2:1$。

8 如图,四边形ABCD∽四边形A'B'C'D',且$\angle A= 62^{\circ}$,$\angle B= 75^{\circ}$,$\angle D'= 140^{\circ}$,AD= 9,A'B'= 11,A'D'= 6,B'C'= 8.

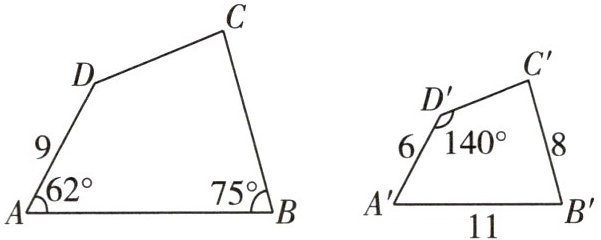
(1)请直接写出:$\angle C= $______°.
(2)求边AB和BC的长.
(1)83
(2)AB=$\frac{33}{2}$，BC=12

答案： 解：
(1) $83$
四边形 $ABCD \backsim$ 四边形 $A'B'C'D' \to \angle D = \angle D' = 140^\circ \to \angle C = 360^\circ - \angle A - \angle B - \angle D = 360^\circ - 62^\circ - 75^\circ - 140^\circ = 83^\circ$。
(2)
∵ 四边形 $ABCD \backsim$ 四边形 $A'B'C'D'$，
∴ $\frac{AB}{A'B'} = \frac{BC}{B'C'} = \frac{AD}{A'D'} = \frac{9}{6}$，
∴ $\frac{AB}{11} = \frac{BC}{8} = \frac{9}{6}$，
∴ $AB = \frac{33}{2}$，$BC = 12$。