《2025年一遍过九年级初中数学上册北师大版》

1 [2023 临沂中考]若菱形的两条对角线长分别为 6 和 8,则该菱形的面积为24.

答案： 24

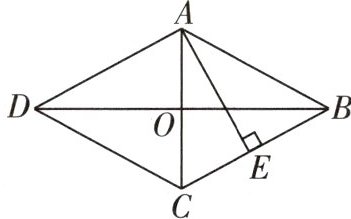
2 教材 P9T3 变式[2024 绥化中考]如图,四边形 ABCD 是菱形,$CD = 5$,$BD = 8$,$AE⊥BC$于点 E,则 AE 的长是____$\frac{24}{5}$.

答案： $\frac{24}{5}$ $\because$ 四边形 $ABCD$ 是菱形，$CD = 5$，$BD = 8$，$\therefore BC = CD = 5$，$BO = DO = 4$，$OA = OC$，$AC \perp BD$，$\therefore \angle BOC = 90^{\circ}$，在 $Rt\triangle OBC$ 中，$OC = \sqrt{BC^{2} - BO^{2}} = \sqrt{5^{2} - 4^{2}} = 3$，$\therefore AC = 2OC = 6$，$\because AE \times BC = \frac{1}{2}BD \times AC = OB \times AC$，（等面积法）$\therefore AE = \frac{OB \times AC}{BC} = \frac{4 \times 6}{5} = \frac{24}{5}$。

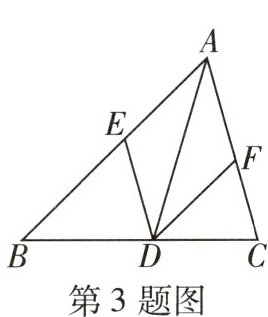
3 [2024 武威十一中期末]如图,$△ABC$中,AD 是角平分线,$DE// AC$交 AB 于 E,$DF// AB$交 AC 于 F,若$AE = 3$,那么四边形 AEDF 的周长为(12)

A. 9
B. 12
C. 15
D. 18

答案： B $\because DE // AC$，$DF // AB$，$\therefore$ 四边形 $AEDF$ 是平行四边形，$\angle EDA = \angle FAD$，$\because AD$ 平分 $\angle BAC$，$\therefore \angle EAD = \angle FAD$，$\therefore \angle EAD = \angle EDA$，$\therefore EA = ED$，$\therefore$ 平行四边形 $AEDF$ 是菱形，$\therefore$ 四边形 $AEDF$ 的周长为 $4AE = 12$。

4 [2024 泉州五中月考]如图,平行四边形 ABCD 中,$∠A = 110^{\circ}$,$AD = DC$,E,F 分别是边 AB 和 BC 的中点,$EP⊥CD$于点 P,连接 EF,PF,则$∠PEF = $(35°)
A.$35^{\circ}$
B.$45^{\circ}$
C.$50^{\circ}$
D.$55^{\circ}$

答案： A 在平行四边形 $ABCD$ 中，$AD = DC$，$\therefore$ 四边形 $ABCD$ 为菱形，$\therefore AB = BC$，$AD // BC$，$\therefore \angle ABC = 180^{\circ} - \angle A = 70^{\circ}$。$\because E$，$F$ 分别为 $AB$，$BC$ 的中点，$\therefore BE = \frac{1}{2}AB$，$BF = \frac{1}{2}BC$，$\therefore BE = BF$，$\therefore \angle BEF = \angle BFE = 55^{\circ}$。$\because PE \perp CD$，$AB // CD$，$\therefore PE \perp AB$，$\therefore \angle PEB = 90^{\circ}$，$\therefore \angle PEF = 90^{\circ} - 55^{\circ} = 35^{\circ}$。

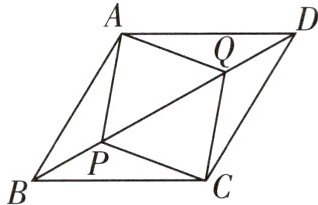
5 如图,在四边形 ABCD 中,$AD// BC$,点 P,Q 是对角线 BD 上不同的两点,若四边形 APCQ 是菱形,则下列说法中不正确的是(

)
A.$BP = DQ$
B.$∠ABD = ∠ADB$
C.$AB// CD$
D.$∠ABP = ∠BAP$

答案：
D 如图，连接 $AC$，$\because$ 四边形 $APCQ$ 是菱形，$\therefore AP = PC = CQ = AQ$，$AQ // PC$，$AC \perp BD$，$\therefore \angle AQP = \angle CPQ$，$\therefore \angle AQD = \angle BPC$。$\because AD // BC$，$\therefore \angle ADQ = \angle CBP$。在 $\triangle ADQ$ 和 $\triangle CBP$ 中，$\left\{\begin{array}{l}\angle ADQ = \angle CBP,\\\angle AQD = \angle CPB,\\AQ = CP,\end{array}\right.$ $\therefore \triangle ADQ \cong \triangle CBP(AAS)$，$\therefore AD = BC$，$BP = DQ$（A 项不合题意）。又 $\because AD // BC$，$\therefore$ 四边形 $ABCD$ 是平行四边形，$\therefore AB = CD$，$AB // CD$（C 项不合题意）。在平行四边形 $ABCD$ 中，$AC \perp BD$，$\therefore$ 平行四边形 $ABCD$ 是菱形，$\therefore AB = AD$，$\therefore \angle ABD = \angle ADB$（B 项不合题意）。

6 教材 P8 做一做变式[2024 太原三十六中月考]如图,两张等宽的纸条交叉叠放在一起,重合部分构成四边形 ABCD.测得 A,B 之间的距离为 6,A,C 之间的距离为 4,则 B,D 之间的距离是( )

A.$4\sqrt{2}$
B. 8
C.$8\sqrt{2}$
D.$4\sqrt{10}$

答案：
C 如图，过点 $A$ 作 $AE \perp BC$ 于点 $E$，$AF \perp CD$ 于点 $F$，连接 $AC$，$BD$ 交于点 $O$，$\because$ 两条纸条宽度相同，$\therefore AE = AF$。$\because AB // CD$，$AD // BC$，$\therefore$ 四边形 $ABCD$ 是平行四边形。$\because S_{\square ABCD} = BC \cdot AE = CD \cdot AF$，$\therefore BC = CD$，$\therefore$ 四边形 $ABCD$ 是菱形，$\therefore AO = CO = \frac{1}{2}AC = \frac{1}{2} \times 4 = 2$，$BO = DO$，$AC \perp BD$。$\because AB = 6$，$\therefore BO = \sqrt{AB^{2} - AO^{2}} = \sqrt{6^{2} - 2^{2}} = 4\sqrt{2}$，$\therefore BD = 8\sqrt{2}$。

7 [2024 哈尔滨中考]四边形 ABCD 的对角线 AC,BD 相交于点 O,$AD// BC$,$OA = OC$,$AB = BC$.
(1)如图 1,求证:四边形 ABCD 是菱形.
(2)如图 2,$AB = AC$,$CH⊥AD$于点 H,交 BD 于点 E,连接 AE,点 G 在 AB 上,连接 EG 交 AC 于点 F,若$∠FEC = 75^{\circ}$,在不添加任何辅助线的情况下,直接写出四条与线段 CE 相等的线段(线段 CE 除外).
AE，DE，AG，CF

答案： （1）证明：$\because AD // BC$，$\therefore \angle ADO = \angle CBO$。
在 $\triangle ADO$ 和 $\triangle CBO$ 中，$\left\{\begin{array}{l}\angle ADO = \angle CBO,\\\angle AOD = \angle COB,\\OA = OC,\end{array}\right.$
$\therefore \triangle ADO \cong \triangle CBO(AAS)$，$\therefore OD = OB$，
$\therefore$ 四边形 $ABCD$ 是平行四边形，
又 $\because AB = BC$，$\therefore$ 四边形 $ABCD$ 是菱形。
（2）解：与线段 $CE$ 相等的线段有 $AE$，$DE$，$AG$，$CF$。
由（1）知：四边形 $ABCD$ 是菱形，$\therefore AB = BC = CD = AD$，$AC \perp BD$。
$\because AB = AC$，$\therefore AB = BC = CD = AD = AC$，
$\therefore \triangle ABC$ 和 $\triangle ADC$ 均为等边三角形，
$\because CH \perp AD$，$\therefore AH = DH$，
$\therefore CH$ 为 $AD$ 的垂直平分线，$\therefore AE = DE$。
同理，$CE = AE$，$\therefore AE = DE = EC$。
$\because \triangle ADC$ 为等边三角形，$CH \perp AD$，
$\therefore \angle ACH = \frac{1}{2}\angle ACD = 30^{\circ}$。
$\because \angle FEC = 75^{\circ}$，$\therefore \angle EFC = 180^{\circ} - \angle ACH - \angle FEC = 75^{\circ}$，
$\therefore \angle EFC = \angle FEC$，$\therefore CF = CE$。
$\because \triangle ABC$ 和 $\triangle ADC$ 均为等边三角形，$\therefore \angle BAC = \angle CAD = 60^{\circ}$，
$\because CE = AE$，$\therefore \angle EAC = \angle ECA = 30^{\circ}$，
$\therefore \angle BAE = \angle BAC + \angle CAE = 90^{\circ}$，$\angle AEC = 180^{\circ} - \angle EAC - \angle ECA = 120^{\circ}$，
$\therefore \angle AEG = \angle AEC - \angle FEC = 45^{\circ}$，$\therefore \triangle AGE$ 为等腰直角三角形，
$\therefore AE = AG$，$\therefore AG = EC$。