《2025年一遍过九年级初中数学上册北师大版》

1 如果$\frac {a+b-c}{c}= \frac {a-b+c}{b}= \frac {-a+b+c}{a}= k$成立,那么k的值为(1或-2)
A. 1
B. -2
C. -2或1
D. 1或2

答案： C 当 $ a + b + c \neq 0 $ 时，由比例的性质，得 $ k = \frac { a + b + c } { a + b + c } = 1 $；当 $ a + b + c = 0 $，即 $ a + b = - c $ 时，$ k = \frac { - 2 c } { c } = - 2 $。综上，$ k $ 的值为 1 或 -2。
易错分析：解答本题时，最容易出现的错误是直接应用等比性质，得出 $ k = 1 $，忽视了等比性质的运用条件。

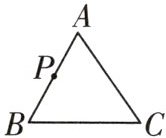
2 [2024菏泽牡丹区期末]如图,$\triangle ABC$中,P是AB边上一点(与A,B不重合),过点P作直线截$\triangle ABC$,所截得的三角形与$\triangle ABC$相似,满足这样条件的直线共有( )

A. 1条
B. 2条
C. 3条
D. 4条

答案：
D 如图 1，作 $ PE // BC $，交 $ AC $ 于点 $ E $，则 $ \triangle APE \backsim \triangle ABC $；如图 2，作 $ PE // AC $，交 $ BC $ 于点 $ E $，则 $ \triangle PBE \backsim \triangle ABC $；如图 3，作 $ PE $，交 $ AC $ 于点 $ E $，使 $ \frac { A E } { A B } = \frac { A P } { A C } $，则 $ \triangle A E P \backsim \triangle A B C $；如图 4，作 $ PE $，交 $ BC $ 于点 $ E $，使 $ \frac { B P } { B C } = \frac { B E } { B A } $，则 $ \triangle E B P \backsim \triangle A B C $。

3 在平面直角坐标系中,原点O是$\triangle ABC$和$\triangle A'B'C'$的位似中心,点A的对应点是点A',点B的对应点是点$B',\triangle ABC$与$\triangle A'B'C'$的面积比是1:9,点A的坐标是(1,0),则点A'的坐标是 ( - 3, 0 ) 或 ( 3, 0 ) ．

答案： $ ( - 3, 0 ) $ 或 $ ( 3, 0 ) $ $ \because \triangle A B C $ 与 $ \triangle A ^ { \prime } B ^ { \prime } C ^ { \prime } $ 的面积比是 $ 1 : 9 $，$ \therefore \triangle A B C $ 与 $ \triangle A ^ { \prime } B ^ { \prime } C ^ { \prime } $ 的相似比是 $ 1 : 3 $。分两种情况，$ \triangle A B C $ 和 $ \triangle A ^ { \prime } B ^ { \prime } C ^ { \prime } $ 在原点 $ O $ 的异侧与 $ \triangle A B C $ 和 $ \triangle A ^ { \prime } B ^ { \prime } C ^ { \prime } $ 在原点 $ O $ 的同侧，$ \therefore $ 将点 $ A $ 的横、纵坐标同时乘以 $ - 3 $ 或 $ 3 $，得点 $ A ^ { \prime } $ 的坐标为 $ ( - 3, 0 ) $ 或 $ ( 3, 0 ) $。
易错分析：当只知道相似比和位似中心时，可以画出两种不同的位似图形，解题时常因只对一种情况进行求解而出错。本题易忽略 $ A ^ { \prime } $ 和 $ A $ 位于点 $ O $ 的异侧的情况。

4 [2024抚州临川一中月考]如图,$AB⊥BD$,$CD⊥BD$,$AB= 6$,$CD= 4$,$BD= 14$,点P在线段BD上移动,当$\triangle PCD与\triangle ABP$相似时,PB的

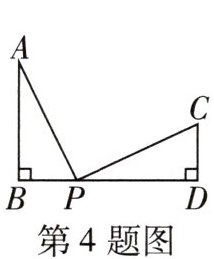
长为____8.4 或 2 或 12．

答案： 8.4 或 2 或 12 设 $ D P = x $，则 $ B P = B D - P D = 14 - x $。$ \because A B \perp B D $，$ C D \perp B D $，$ \therefore \angle B = \angle D = 90 ^ { \circ } $，$ \therefore $ 当 $ \frac { A B } { C D } = \frac { B P } { D P } $ 时，$ \triangle A B P \backsim \triangle C D P $，即 $ \frac { 6 } { 4 } = \frac { 14 - x } { x } $，解得 $ x = \frac { 28 } { 5 } $，$ \therefore B P = 14 - \frac { 28 } { 5 } = 8.4 $；当 $ \frac { A B } { P D } = \frac { B P } { D C } $ 时，$ \triangle A B P \backsim \triangle P D C $，即 $ \frac { 6 } { x } = \frac { 14 - x } { 4 } $，整理，得 $ x ^ { 2 } - 14 x + 24 = 0 $，解得 $ x _ { 1 } = 2 $，$ x _ { 2 } = 12 $，$ \therefore B P = 14 - 2 = 12 $ 或 $ B P = 14 - 12 = 2 $，$ \therefore $ 当 $ P B $ 为 8.4 或 2 或 12 时，$ \triangle P C D $ 与 $ \triangle A B P $ 相似。

5 将三角形纸片($\triangle ABC$)按如图所示的方式折叠,使点B落在边AC上,记为点$B'$,折痕为EF．已知$AB= AC= 3$,$BC= 4$,若$\triangle B'FC与\triangle ABC$相似,则BF的长是$\frac{12}{7}$或2．

答案： $ \frac { 12 } { 7 } $ 或 2 设 $ B F = x $，则 $ F C = 4 - x $，由折叠的性质知 $ B ^ { \prime } F = B F = x $。分两种情况：①当 $ B ^ { \prime } F = B ^ { \prime } C $ 时，有 $ \triangle B ^ { \prime } F C \backsim \triangle ABC $，则 $ B ^ { \prime } F : A B = F C : B C $，即 $ x : 3 = ( 4 - x ) : 4 $，解得 $ x = \frac { 12 } { 7 } $；②当 $ B ^ { \prime } F = F C $ 时，有 $ \triangle B ^ { \prime } F C \backsim \triangle B A C $，则 $ B ^ { \prime } F : B A = F C : A C $，即 $ x : 3 = ( 4 - x ) : 3 $，解得 $ x = 2 $。综上，$ B F $ 的长是 $ \frac { 12 } { 7 } $ 或 2。

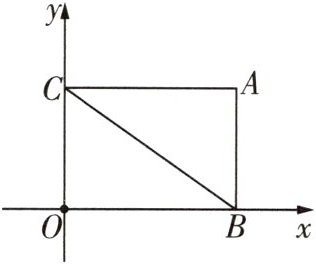
6 [2025盘锦双台子区联考]如图,在平面直角坐标系中,矩形ABOC的边OB,OC分别在x轴、y轴的正半轴上,点A的坐标为$(8,6)$,点P在矩形ABOC的内部,点E在BO边上,且满足$\triangle PBE\backsim \triangle CBO$,当$\triangle APC$是等腰三角形时,点P的坐标为____．

答案：
$ ( \frac { 32 } { 5 }, \frac { 6 } { 5 } ) $ 或 $ ( 4, 3 ) $ $ \because $ 点 $ P $ 在矩形 $ A B O C $ 的内部，且 $ \triangle A P C $ 是等腰三角形，$ \therefore $ 点 $ P $ 在 $ A C $ 的垂直平分线上或在以点 $ C $ 为圆心 $ A C $ 为半径的圆弧上。当点 $ P $ 在 $ A C $ 的垂直平分线上时，点 $ P $ 同时在 $ B C $ 上，$ A C $ 的垂直平分线与 $ B O $ 的交点即是 $ E $，如图 1，$ \because P E \perp B O $，$ C O \perp B O $，$ \therefore P E // C O $，$ \therefore \angle B P E = \angle B C O $，$ \angle B E P = \angle B O C $，$ \therefore \triangle P B E \backsim \triangle C B O $，$ \therefore \frac { P E } { C O } = \frac { B E } { B O } $，$ \because $ 四边形 $ A B O C $ 是矩形，点 $ A $ 的坐标为 $ ( 8, 6 ) $，$ \therefore $ 点 $ P $ 的横坐标为 4，$ O C = 6 $，$ B O = 8 $，$ B E = 4 $，$ \therefore \frac { P E } { 6 } = \frac { 4 } { 8 } $，解得 $ P E = 3 $，$ \therefore $ 点 $ P ( 4, 3 ) $。当点 $ P $ 在以点 $ C $ 为圆心 $ A C $ 为半径的圆弧上时，如图 2，圆弧与 $ B C $ 的交点为 $ P $，过点 $ P $ 作 $ P E \perp B O $ 于点 $ E $。$ \because C O \perp B O $，$ \therefore P E // C O $，$ \therefore \angle B P E = \angle B C O $，$ \angle B E P = \angle B O C $，$ \therefore \triangle P B E \backsim \triangle C B O $，$ \therefore \frac { P E } { C O } = \frac { B E } { B O } = \frac { B P } { B C } $。$ \because $ 四边形 $ A B O C $ 是矩形，点 $ A $ 的坐标为 $ ( 8, 6 ) $，$ \therefore A C = B O = 8 $，$ C P = 8 $，$ A B = O C = 6 $，$ \therefore B C = \sqrt { B O ^ { 2 } + O C ^ { 2 } } = \sqrt { 8 ^ { 2 } + 6 ^ { 2 } } = 10 $，$ \therefore B P = 2 $。$ \therefore \frac { P E } { 6 } = \frac { B E } { 8 } = \frac { 2 } { 10 } $，解得 $ P E = \frac { 6 } { 5 } $，$ B E = \frac { 8 } { 5 } $，$ \therefore O E = 8 - \frac { 8 } { 5 } = \frac { 32 } { 5 } $，$ \therefore $ 点 $ P ( \frac { 32 } { 5 }, \frac { 6 } { 5 } ) $。综上，点 $ P $ 的坐标为 $ ( \frac { 32 } { 5 }, \frac { 6 } { 5 } ) $ 或 $ ( 4, 3 ) $。

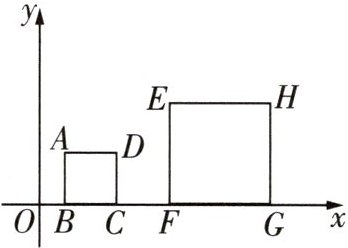
7 如图,在平面直角坐标系中,正方形ABCD的边BC在x轴上,其中点A的坐标为$(1,2)$,正方形EFGH的边FG在x轴上,且点H的坐标为$(9,4)$．已知正方形ABCD与正方形EFGH是位似图形,求位似中心的坐标．

答案：
解：分两种情况讨论：
①如图 1，连接 $ H D $ 并延长交 $ x $ 轴于点 $ P $，则点 $ P $ 为正方形 $ A B C D $ 与正方形 $ E F G H $ 的位似中心，$ \because $ 四边形 $ A B C D $ 为正方形，点 $ A $ 的坐标为 $ ( 1, 2 ) $，$ \therefore $ 点 $ D $ 的坐标为 $ ( 3, 2 ) $，$ \because \angle D C P = \angle H G P = 90 ^ { \circ } $，$ \angle D P C = \angle H P G $，$ \therefore \triangle P C D \backsim \triangle P G H $，$ \therefore \frac { P C } { P G } = \frac { C D } { G H } $，即 $ \frac { O P + 3 } { O P + 9 } = \frac { 2 } { 4 } $，$ \therefore O P = 3 $，$ \therefore $ 正方形 $ A B C D $ 与正方形 $ E F G H $ 的位似中心的坐标是 $ ( - 3, 0 ) $；

②如图 2，连接 $ C E $，$ D F $ 交于点 $ P $，由题意得 $ C ( 3, 0 ) $，$ E ( 5, 4 ) $，$ D ( 3, 2 ) $，$ F ( 5, 0 ) $，易求出直线 $ D F $ 的函数表达式为 $ y = - x + 5 $，直线 $ C E $ 的函数表达式为 $ y = 2 x - 6 $，联立，得 $ \left\{ \begin{array} { l } { y = - x + 5 }, \\ { y = 2 x - 6 }, \end{array} \right. $ 解得 $ \left\{ \begin{array} { l } { x = \frac { 11 } { 3 } }, \\ { y = \frac { 4 } { 3 } }, \end{array} \right. $ $ \therefore $ 直线 $ D F $，$ C E $ 的交点 $ P $ 的坐标为 $ ( \frac { 11 } { 3 }, \frac { 4 } { 3 } ) $，$ \therefore $ 正方形 $ A B C D $ 与正方形 $ E F G H $ 的位似中心的坐标是 $ ( \frac { 11 } { 3 }, \frac { 4 } { 3 } ) $。
综上，位似中心的坐标为 $ ( - 3, 0 ) $ 或 $ ( \frac { 11 } { 3 }, \frac { 4 } { 3 } ) $。