第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
1 [2024济南中考]3月14日是国际数学节.某学校在今年国际数学节策划了“竞速华容道”“玩转幻方”和“巧解鲁班锁”三个挑战活动,如果小红和小丽每人随机选择参加其中一个活动,那么她们恰好选到同一个活动的概率是( )
A. $\frac{1}{9}$
B. $\frac{1}{6}$
C. $\frac{1}{3}$
D. $\frac{2}{3}$
A. $\frac{1}{9}$
B. $\frac{1}{6}$
C. $\frac{1}{3}$
D. $\frac{2}{3}$
答案:
C 将“竞速华容道”“玩转幻方”和“巧解鲁班锁”三个活动分别记为 A,B,C,列表如下:
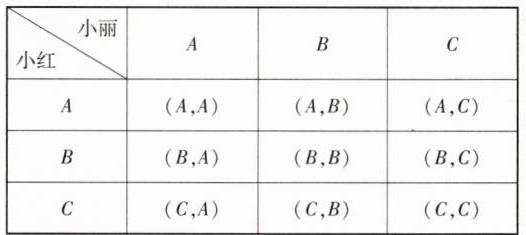
由表格可知,共有 9 种等可能的结果,小红和小丽恰好选到同一个活动的结果有 3 种,所以小红和小丽恰好选到同一个活动的概率为 $\frac{3}{9}=\frac{1}{3}$.
策略点拨
用列表法求概率的步骤
对于两步试验(两个条件或两次操作)且可能出现的结果比较多时,用直接列举法易出错,为了不重不漏地列出所有可能的结果,用列表法比较好.用列表法求概率的步骤:
(1)列表,即通过表格记数,确定所有可能的结果数 n 和关注的结果数 m 的值;
(2)计算,利用概率公式 $P=\frac{m}{n}$ 计算出事件的概率.
C 将“竞速华容道”“玩转幻方”和“巧解鲁班锁”三个活动分别记为 A,B,C,列表如下:

由表格可知,共有 9 种等可能的结果,小红和小丽恰好选到同一个活动的结果有 3 种,所以小红和小丽恰好选到同一个活动的概率为 $\frac{3}{9}=\frac{1}{3}$.
策略点拨
用列表法求概率的步骤
对于两步试验(两个条件或两次操作)且可能出现的结果比较多时,用直接列举法易出错,为了不重不漏地列出所有可能的结果,用列表法比较好.用列表法求概率的步骤:
(1)列表,即通过表格记数,确定所有可能的结果数 n 和关注的结果数 m 的值;
(2)计算,利用概率公式 $P=\frac{m}{n}$ 计算出事件的概率.
2 [2024牡丹江中考]某校八年级3班承担下周学校升旗任务,老师从备选的甲、乙、丙、丁四名同学中,选择两名担任升旗手,则甲、乙两名同学同时被选中的概率是( )
A. $\frac{1}{6}$
B. $\frac{1}{8}$
C. $\frac{1}{4}$
D. $\frac{2}{3}$
A. $\frac{1}{6}$
B. $\frac{1}{8}$
C. $\frac{1}{4}$
D. $\frac{2}{3}$
答案:
A 列表如下:

由表格可知,共有 12 种等可能的结果,其中甲、乙两名同学同时被选中的结果有 2 种,则甲、乙两名同学同时被选中的概率是 $\frac{2}{12}=\frac{1}{6}$.
A 列表如下:

由表格可知,共有 12 种等可能的结果,其中甲、乙两名同学同时被选中的结果有 2 种,则甲、乙两名同学同时被选中的概率是 $\frac{2}{12}=\frac{1}{6}$.
3 [2023潍坊中考]投掷两枚骰子,朝上一面的点数之和为7的概率是______.
答案:
$\frac{1}{6}$ 列表如下:
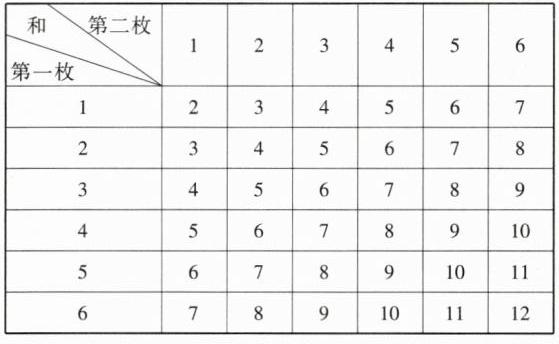
由表格可知,共有 36 种等可能的结果,其中朝上一面的点数之和为 7 的结果有 6 种,故朝上一面的点数之和为 7 的概率是 $\frac{6}{36}=\frac{1}{6}$.
$\frac{1}{6}$ 列表如下:

由表格可知,共有 36 种等可能的结果,其中朝上一面的点数之和为 7 的结果有 6 种,故朝上一面的点数之和为 7 的概率是 $\frac{6}{36}=\frac{1}{6}$.
(1)将球搅匀,从中任意摸出1个球,摸到白球的概率是
(2)将球搅匀,从中任意摸出1个球,记录颜色后放回、搅匀,再从中任意摸出1个球.求2次摸到的球颜色不同的概率.
解:列表如下:
第一次第二次 白 红 绿
白 (白,白) (白,红) (白,绿)
红 (红,白) (红,红) (红,绿)
绿 (绿,白) (绿,红) (绿,绿)
由表格可知,共有 9 种等可能的结果,其中 2 次摸到的球颜色不同的结果有 6 种,
所以 2 次摸到的球颜色不同的概率为
$\frac{1}{3}$
.(2)将球搅匀,从中任意摸出1个球,记录颜色后放回、搅匀,再从中任意摸出1个球.求2次摸到的球颜色不同的概率.
解:列表如下:
第一次第二次 白 红 绿
白 (白,白) (白,红) (白,绿)
红 (红,白) (红,红) (红,绿)
绿 (绿,白) (绿,红) (绿,绿)
由表格可知,共有 9 种等可能的结果,其中 2 次摸到的球颜色不同的结果有 6 种,
所以 2 次摸到的球颜色不同的概率为
$\frac{2}{3}$
.
答案:
解:
(1)$\frac{1}{3}$
(2)列表如下:
第一次第二次 白 红 绿
白 (白,白) (白,红) (白,绿)
红 (红,白) (红,红) (红,绿)
绿 (绿,白) (绿,红) (绿,绿)
由表格可知,共有 9 种等可能的结果,其中 2 次摸到的球颜色不同的结果有 6 种,
所以 2 次摸到的球颜色不同的概率为 $\frac{6}{9}=\frac{2}{3}$.
(1)$\frac{1}{3}$
(2)列表如下:
第一次第二次 白 红 绿
白 (白,白) (白,红) (白,绿)
红 (红,白) (红,红) (红,绿)
绿 (绿,白) (绿,红) (绿,绿)
由表格可知,共有 9 种等可能的结果,其中 2 次摸到的球颜色不同的结果有 6 种,
所以 2 次摸到的球颜色不同的概率为 $\frac{6}{9}=\frac{2}{3}$.
5 [2024山西中考]一个不透明的盒子里装有一个红球、一个白球和一个绿球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后不放回,再从中随机摸出一个球,则两次摸到的球恰好有一个红球的概率是( )
A. $\frac{1}{3}$
B. $\frac{2}{3}$
C. $\frac{4}{9}$
D. $\frac{5}{9}$
A. $\frac{1}{3}$
B. $\frac{2}{3}$
C. $\frac{4}{9}$
D. $\frac{5}{9}$
答案:
B 画树状图如下:

由树状图可知,共有 6 种等可能的结果,其中两次摸到的球恰好有一个红球的结果有(红,白),(红,绿),(白,红),(绿,红),共 4 种,所以两次摸到的球恰好有一个红球的概率为 $\frac{4}{6}=\frac{2}{3}$.
策略点拨
用画树状图法求概率的步骤
(1)将试验中第一步可能产生的 $n_1$ 种结果不分先后地写在第一层.
(2)在第一步产生的 $n_1$ 种结果下画出分支,分别写出第二步可能产生的 $n_2$ 种结果,以此类推.
(3)写出所有等可能的结果,得到等可能结果的数量,再找出符合要求的结果的数量,利用等可能事件的概率计算公式计算概率.
B 画树状图如下:

由树状图可知,共有 6 种等可能的结果,其中两次摸到的球恰好有一个红球的结果有(红,白),(红,绿),(白,红),(绿,红),共 4 种,所以两次摸到的球恰好有一个红球的概率为 $\frac{4}{6}=\frac{2}{3}$.
策略点拨
用画树状图法求概率的步骤
(1)将试验中第一步可能产生的 $n_1$ 种结果不分先后地写在第一层.
(2)在第一步产生的 $n_1$ 种结果下画出分支,分别写出第二步可能产生的 $n_2$ 种结果,以此类推.
(3)写出所有等可能的结果,得到等可能结果的数量,再找出符合要求的结果的数量,利用等可能事件的概率计算公式计算概率.
6 [2023德阳中考]在6,7,8,9四个数字中任意选取两个数字,则这两个数字之和为奇数的概率是( )
A. $\frac{1}{3}$
B. $\frac{1}{2}$
C. $\frac{2}{3}$
D. $\frac{1}{4}$
A. $\frac{1}{3}$
B. $\frac{1}{2}$
C. $\frac{2}{3}$
D. $\frac{1}{4}$
答案:
C 画树状图如下:

(注意:从四个数字中任意选取两个,属于“不放回”抽取)
由树状图可知,共有 12 种等可能的结果,这两个数字之和为奇数的结果有 8 种,所以这两个数字之和为奇数的概率为 $\frac{8}{12}=\frac{2}{3}$.
C 画树状图如下:

(注意:从四个数字中任意选取两个,属于“不放回”抽取)
由树状图可知,共有 12 种等可能的结果,这两个数字之和为奇数的结果有 8 种,所以这两个数字之和为奇数的概率为 $\frac{8}{12}=\frac{2}{3}$.
7 教材P61随堂练习变式[2024德州中考]衣橱里挂着3套不同颜色的服装,同一套服装的上衣与裤子的颜色相同,若从衣橱里各任取一件上衣和一条裤子,则它们取自同一套的概率是______.
答案:
$\frac{1}{3}$ 记 3 件上衣分别为 A,B,C,对应的裤子分别为 a,b,c,画树状图如下:

由树状图可知,共有 9 种等可能结果,其中取自同一套的结果有 3 种,所以它们取自同一套的概率为 $\frac{3}{9}=\frac{1}{3}$.
$\frac{1}{3}$ 记 3 件上衣分别为 A,B,C,对应的裤子分别为 a,b,c,画树状图如下:

由树状图可知,共有 9 种等可能结果,其中取自同一套的结果有 3 种,所以它们取自同一套的概率为 $\frac{3}{9}=\frac{1}{3}$.
8 [2024淮安中考]历史文化名城淮安有着丰富的旅游资源.小明计划假期来淮安游玩,他打算从3个人文景点(A. 周恩来纪念馆;B. 吴承恩故居;C. 河下古镇)中随机选取一个,再从2个自然景点(D. 金湖水上森林;E. 铁山寺国家森林公园)中随机选取一个.
(1)小明从人文景点中选中河下古镇的概率是______;
(2)用树状图或列表的方法求小明恰好选中周恩来纪念馆和铁山寺国家森林公园的概率.
(1)小明从人文景点中选中河下古镇的概率是______;
(2)用树状图或列表的方法求小明恰好选中周恩来纪念馆和铁山寺国家森林公园的概率.
答案:
解:
(1)$\frac{1}{3}$
(2)画树状图如下:

由树状图可知,共有 6 种等可能的结果,其中小明恰好选中周恩来纪念馆和铁山寺国家森林公园的结果有 1 种,
所以小明恰好选中周恩来纪念馆和铁山寺国家森林公园的概率为 $\frac{1}{6}$.
策略点拨
用画树状图法或列表法求事件的概率的关键
用画树状图法或列表法求事件的概率时,要根据情况选用合适的方法:
(1)当试验涉及两个因素时,可以用列表法也可以用画树状图法,当结果数目较多时,用列表法较简便;
(2)当试验涉及三个或更多个因素时,应采用画树状图法.用画树状图法或列表法求概率的关键是不重不漏地列举出所有等可能的结果,求出所关注的事件包含的结果数,该结果数与总结果数的比值就是所求事件的概率.
解:
(1)$\frac{1}{3}$
(2)画树状图如下:

由树状图可知,共有 6 种等可能的结果,其中小明恰好选中周恩来纪念馆和铁山寺国家森林公园的结果有 1 种,
所以小明恰好选中周恩来纪念馆和铁山寺国家森林公园的概率为 $\frac{1}{6}$.
策略点拨
用画树状图法或列表法求事件的概率的关键
用画树状图法或列表法求事件的概率时,要根据情况选用合适的方法:
(1)当试验涉及两个因素时,可以用列表法也可以用画树状图法,当结果数目较多时,用列表法较简便;
(2)当试验涉及三个或更多个因素时,应采用画树状图法.用画树状图法或列表法求概率的关键是不重不漏地列举出所有等可能的结果,求出所关注的事件包含的结果数,该结果数与总结果数的比值就是所求事件的概率.
查看更多完整答案,请扫码查看


