《2025年一遍过九年级初中数学上册北师大版》

8 [2024张家口宣化区期末]如图,已知$AB// CD// EF$,那么下列结论不正确的是(B)

A. $\frac {AD}{DF}= \frac {BC}{CE}$
B. $\frac {BC}{CE}= \frac {DF}{AD}$
C. $\frac {CE}{EB}= \frac {DF}{AF}$
D. $\frac {BC}{BE}= \frac {AD}{AF}$

答案： 8 B
∵AB//CD//EF,
∴$\frac{AD}{DF}$=$\frac{BC}{CE}$,$\frac{CE}{BE}$=$\frac{DF}{AF}$,$\frac{BC}{BE}$=$\frac{AD}{AF}$.

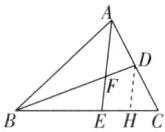
9 [2025天水月考]如图,在$\triangle ABC$中,D是AC的中点,点F在BD上,连接AF并延长交BC于点E,若$BF:FD= 3:1$,$BC= 10$,则CE的长为( )
A. 3
B. 4
C. 5
D. $\frac {10}{3}$

答案：
9 B 如图, 过点D作DH//AE, 交BC于点H, 则$\frac{CH}{HE}$=$\frac{CD}{DA}$ = 1,$\frac{BE}{EH}$=$\frac{BF}{FD}$ = 3,
∴$\frac{BE}{EC}$=$\frac{3}{2}$,
∵BC = 10,
∴CE = 4.

归纳总结
当题目中已知三角形某边的中点时，过该点作其他边的平行线构造中位线是常用的辅助线的作法

10 [2024咸阳月考]如图1,装有某种液体的工业用桶中放有一根搅拌棍.工人师傅为了解桶内所装液体的体积,先在搅拌棍所处桶孔位置做好标记点A,并取出；然后测得搅拌棍接触到液体部分$BD= 1m$,搅拌棍A到底端D处的长度为1.5m,最后测量出桶的高AE为1.2m,圆桶内壁的底面直径DE为1m.已知桶内的液面与桶底面平行,其平面示意图如图2所示,$BC// DE$.根据以上数据计算出桶内所装液体的体积(结果保留π)为____$\frac{π}{5}$m³.

答案： 10 $\frac{π}{5}$m³
∵BC//DE,
∴$\frac{BD}{AD}$=$\frac{CE}{AE}$,
∴$\frac{1}{1.5}$=$\frac{CE}{1.2}$, 解得CE = 0.8m,
∴桶内所装液体的体积为π×($\frac{1}{2}$)²×0.8 = $\frac{π}{5}$(m³).

11 如图,在$\triangle ABC$中,点D为AC上一点,且$\frac {CD}{AD}= \frac {1}{2}$,过点D作$DE// BC$交AB于点E,连接CE,过点D作$DF// CE$交AB于点F.若$AB= 15$,则$EF= $$\frac{10}{3}$.

答案： 11 $\frac{10}{3}$
∵DE//BC,
∴$\frac{AD}{AC}$=$\frac{AE}{AB}$.
∵$\frac{CD}{AD}$=$\frac{1}{2}$,
∴$\frac{AD}{AC}$=$\frac{2}{3}$,
∴$\frac{AE}{AB}$=$\frac{2}{3}$, 又
∵AB = 15,
∴AE = 10.
∵DF//CE,
∴$\frac{AF}{AE}$=$\frac{AD}{AC}$, 即 $\frac{AF}{10}$=$\frac{2}{3}$, 解得AF = $\frac{20}{3}$, 则EF = AE - AF = $\frac{10}{3}$.

12 [2024洛阳月考]如图,AD是$\triangle ABC$的中线,P为AD上任意一点,连接BP并延长,交AC于点F,连接CP并延长,交AB于点E,连接EF.求证：$AP:PD= 2AE:EB$.

答案：
12 证明: 如图, 过点D作DN//CE, 交AB于点N.
∵AD是△ABC的中线,
∴DC = DB.
∵DN//CE,
∴$\frac{BN}{EN}$=$\frac{BD}{DC}$ = 1,
∴EN = NB = $\frac{1}{2}$EB.
∵PE//ND,
∴AP:PD = AE:EN,

即AP:PD = AE:$\frac{1}{2}$EB,
∴AP:PD = 2AE:EB.

13 推理能力[2025朝阳月考]阅读与计算,请阅读以下材料,并完成相应的问题.
角平分线分线段成比例定理,如图1,在$\triangle ABC$中,AD平分$∠BAC$,则$\frac {AB}{AC}= \frac {BD}{CD}$.下面是这个定理的部分证明过程.
证明：如图2,过点C作$CE// DA$,交线段BA的延长线于点E……
任务：(1)请按照上面的证明思路,写出该证明的剩余部分；
∵CE//AD,∴$\frac{BD}{CD}$=$\frac{AB}{EA}$,∠2 = ∠ACE,∠1 = ∠E.
∵∠1 = ∠2,∴∠ACE = ∠E,∴AE = AC,
∴$\frac{AB}{AC}$=$\frac{BD}{CD}$.(2)如图3,已知$Rt\triangle ABC$中,$AB= 6$,$BC= 8$,$∠ABC= 90^{\circ }$,AD平分$∠BAC$,求$\triangle ABD$的周长.
∵AB = 6,BC = 8,∠ABC = 90°,∴AC = 10,
∵AD平分∠BAC,∴$\frac{AC}{AB}$=$\frac{CD}{BD}$,
∴$\frac{10}{6}$=$\frac{CD}{BD}$,∴BD = $\frac{3}{5}$CD,
∵BD + CD = BC = 8,∴$\frac{3}{5}$CD + CD = 8,
∴CD = 5,∴BD = 3,
∴AD = $\sqrt{BD^{2}+AB^{2}}$ = $\sqrt{3^{2}+6^{2}}$ = 3$\sqrt{5}$,
∴△ABD的周长为3 + 6 + 3$\sqrt{5}$ = 9 + 3$\sqrt{5}$.

答案： 13 解:
(1)
∵CE//AD,
∴$\frac{BD}{CD}$=$\frac{AB}{EA}$,∠2 = ∠ACE,∠1 = ∠E.
∵∠1 = ∠2,
∴∠ACE = ∠E,
∴AE = AC,
∴$\frac{AB}{AC}$=$\frac{BD}{CD}$.
(2)
∵AB = 6,BC = 8,∠ABC = 90°,
∴AC = 10,
∵AD平分∠BAC,
∴$\frac{AC}{AB}$=$\frac{CD}{BD}$,
∴$\frac{10}{6}$=$\frac{CD}{BD}$,
∴BD = $\frac{3}{5}$CD,
∵BD + CD = BC = 8,
∴$\frac{3}{5}$CD + CD = 8,
∴CD = 5,
∴BD = 3,
∴AD = $\sqrt{BD^{2}+AB^{2}}$ = $\sqrt{3^{2}+6^{2}}$ = 3$\sqrt{5}$,
∴△ABD的周长为3 + 6 + 3$\sqrt{5}$ = 9 + 3$\sqrt{5}$.