第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
3 [2025成都双流区月考]在菱形ABCD中,∠ABC= 60°,P是直线BD(不与点B,D重合)上一动点,以AP为边向右侧作等边三角形APE(A,P,E按逆时针排列),点E的位置随点P的位置变化而变化.
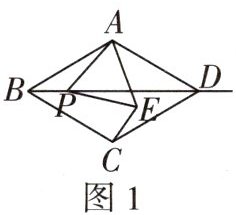
(1)如图1,当点P在线段BD上,且点E在菱形ABCD内部或边上时,连接CE,则BP与CE的数量关系是______,BC与CE的位置关系是______.
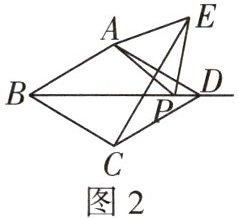
(2)如图2,当点P在线段BD上,且点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由.


(1)如图1,当点P在线段BD上,且点E在菱形ABCD内部或边上时,连接CE,则BP与CE的数量关系是______,BC与CE的位置关系是______.
(2)如图2,当点P在线段BD上,且点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由.
答案:
解:
(1)$BP = CE$ $CE ⊥ BC$
如图 1,连接 $AC$。
∵ 四边形 $ABCD$ 是菱形,$∠ABC = 60^{\circ}$,
∴ $△ABC$ 是等边三角形,$∠ABD = ∠CBD = 30^{\circ}$,
∴ $AB = AC$,$∠ACB = ∠BAC = 60^{\circ}$。
∵ $△APE$ 是等边三角形,
∴ $AP = AE$,$∠PAE = 60^{\circ}$。
∵ $∠BAC = ∠PAE$,
∴ $∠BAP + ∠PAC = ∠CAE + ∠PAC$,
∴ $∠BAP = ∠CAE$,
∴ $△BAP \cong △CAE(SAS)$,
∴ $BP = CE$,$∠ABP = ∠ACE = 30^{\circ}$,
∴ $∠BCE = ∠ACB + ∠ACE = 60^{\circ} + 30^{\circ} = 90^{\circ}$,
∴ $CE ⊥ BC$。

(2)
(1)中结论仍然成立。理由如下:
如图 2,连接 $AC$,
∵ 四边形 $ABCD$ 是菱形,$∠ABC = 60^{\circ}$,
∴ $∠ABD = ∠CBD = 30^{\circ}$,$△ABC$ 为等边三角形,
∴ $AB = AC$,$∠ACB = ∠BAC = 60^{\circ}$,
∵ $△APE$ 是等边三角形,
∴ $AP = AE$,$∠EAP = 60^{\circ}$。
∵ $∠BAP = ∠BAC + ∠CAP = 60^{\circ} + ∠CAP$,$∠CAE = ∠EAP + ∠CAP = 60^{\circ} + ∠CAP$,
∴ $∠BAP = ∠CAE$,
在 $△ABP$ 和 $△ACE$ 中,$\left\{\begin{array}{l} AB = AC,\\ ∠BAP = ∠CAE,\\ AP = AE,\end{array}\right.$
∴ $△ABP \cong △ACE(SAS)$,
∴ $BP = CE$,$∠ACE = ∠ABP = 30^{\circ}$,
∴ $∠BCE = ∠ACB + ∠ACE = 60^{\circ} + 30^{\circ} = 90^{\circ}$,
∴ $CE ⊥ BC$。

解:
(1)$BP = CE$ $CE ⊥ BC$
如图 1,连接 $AC$。
∵ 四边形 $ABCD$ 是菱形,$∠ABC = 60^{\circ}$,
∴ $△ABC$ 是等边三角形,$∠ABD = ∠CBD = 30^{\circ}$,
∴ $AB = AC$,$∠ACB = ∠BAC = 60^{\circ}$。
∵ $△APE$ 是等边三角形,
∴ $AP = AE$,$∠PAE = 60^{\circ}$。
∵ $∠BAC = ∠PAE$,
∴ $∠BAP + ∠PAC = ∠CAE + ∠PAC$,
∴ $∠BAP = ∠CAE$,
∴ $△BAP \cong △CAE(SAS)$,
∴ $BP = CE$,$∠ABP = ∠ACE = 30^{\circ}$,
∴ $∠BCE = ∠ACB + ∠ACE = 60^{\circ} + 30^{\circ} = 90^{\circ}$,
∴ $CE ⊥ BC$。

(2)
(1)中结论仍然成立。理由如下:
如图 2,连接 $AC$,
∵ 四边形 $ABCD$ 是菱形,$∠ABC = 60^{\circ}$,
∴ $∠ABD = ∠CBD = 30^{\circ}$,$△ABC$ 为等边三角形,
∴ $AB = AC$,$∠ACB = ∠BAC = 60^{\circ}$,
∵ $△APE$ 是等边三角形,
∴ $AP = AE$,$∠EAP = 60^{\circ}$。
∵ $∠BAP = ∠BAC + ∠CAP = 60^{\circ} + ∠CAP$,$∠CAE = ∠EAP + ∠CAP = 60^{\circ} + ∠CAP$,
∴ $∠BAP = ∠CAE$,
在 $△ABP$ 和 $△ACE$ 中,$\left\{\begin{array}{l} AB = AC,\\ ∠BAP = ∠CAE,\\ AP = AE,\end{array}\right.$
∴ $△ABP \cong △ACE(SAS)$,
∴ $BP = CE$,$∠ACE = ∠ABP = 30^{\circ}$,
∴ $∠BCE = ∠ACB + ∠ACE = 60^{\circ} + 30^{\circ} = 90^{\circ}$,
∴ $CE ⊥ BC$。

4 [2024韶关期中节选]在正方形ABCD中,点O是对角线AC的中点,点P是线段AO上的一个动点(不与点A,O重合),过点P作PE⊥PB,交边CD于点E.
(1)如图1,求证:PE= PB.
(2)如图2,若正方形ABCD的边长为2,过点E作EF⊥AC于点F,在点P运动的过程中,PF的长度是否发生变化?若不变,试求出PF的长;若变化,请说明理由.
(3)用等式表示线段PC,PA,EC之间的数量关系.
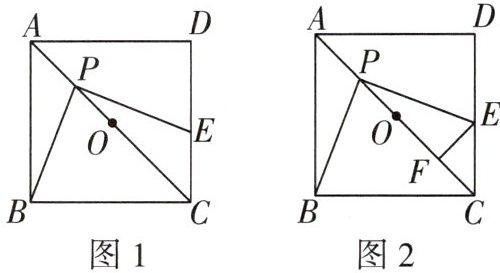
(1)如图1,求证:PE= PB.
(2)如图2,若正方形ABCD的边长为2,过点E作EF⊥AC于点F,在点P运动的过程中,PF的长度是否发生变化?若不变,试求出PF的长;若变化,请说明理由.
(3)用等式表示线段PC,PA,EC之间的数量关系.

答案:
(1)证明:如图 1,过点 $P$ 作 $MN // AD$,交 $AB$ 于点 $M$,交 $CD$ 于点 $N$。
∵ $PB ⊥ PE$,
∴ $∠BPE = 90^{\circ}$,
∴ $∠MPB + ∠EPN = 90^{\circ}$。
∵ 四边形 $ABCD$ 是正方形,
∴ $∠BAD = ∠D = 90^{\circ}$。
∵ $AD // MN$,
∴ $∠BMP = ∠BAD = 90^{\circ}$,$∠PNE = ∠D = 90^{\circ}$,
∴ $∠MPB + ∠MBP = 90^{\circ}$,
∴ $∠EPN = ∠MBP$。
在 $Rt△PNC$ 中,$∠PCN = 45^{\circ}$,
∴ $△PNC$ 是等腰直角三角形,
∴ $PN = CN$,
∴ $BM = CN = PN$。
在 $△BMP$ 和 $△PNE$ 中,$\left\{\begin{array}{l} ∠PBM = ∠EPN,\\ BM = PN,\\ ∠BMP = ∠PNE,\end{array}\right.$
∴ $△BMP \cong △PNE$,
∴ $PB = PE$。

(2)解:在点 $P$ 运动的过程中,$PF$ 的长度不发生变化。理由如下:
如图 2,连接 $OB$。
∵ 点 $O$ 是正方形 $ABCD$ 对角线 $AC$ 的中点,
∴ $OB ⊥ AC$,
∴ $∠AOB = 90^{\circ}$,
∴ $∠OBP + ∠BPO = 90^{\circ}$。
∵ $∠BPE = 90^{\circ}$,
∴ $∠BPO + ∠FPE = 90^{\circ}$,
∴ $∠OBP = ∠FPE$。
∵ $EF ⊥ AC$,
∴ $∠EFP = ∠AOB = 90^{\circ}$。
由
(1)得 $PB = PE$。
在 $△OBP$ 和 $△FPE$ 中,$\left\{\begin{array}{l} ∠OBP = ∠FPE,\\ ∠BOP = ∠PFE,\\ PB = EP,\end{array}\right.$
∴ $△OBP \cong △FPE(AAS)$,
∴ $OB = PF$。
∵ $AB = 2$,$△ABO$ 是等腰直角三角形,
∴ $OB = \sqrt{2}$,
∴ $PF$ 的长为 $\sqrt{2}$。

(3)解:$PC = PA + \sqrt{2}EC$。
如图 1,
∵ $∠BAC = 45^{\circ}$,
∴ $△AMP$ 是等腰直角三角形,
∴ $PA = \sqrt{2}PM$。
由
(1)知 $PM = NE$,
∴ $PA = \sqrt{2}NE$。
∵ $△PCN$ 是等腰直角三角形,
∴ $PC = \sqrt{2}NC = \sqrt{2}(NE + EC) = \sqrt{2}NE + \sqrt{2}EC = PA + \sqrt{2}EC$。
(1)证明:如图 1,过点 $P$ 作 $MN // AD$,交 $AB$ 于点 $M$,交 $CD$ 于点 $N$。
∵ $PB ⊥ PE$,
∴ $∠BPE = 90^{\circ}$,
∴ $∠MPB + ∠EPN = 90^{\circ}$。
∵ 四边形 $ABCD$ 是正方形,
∴ $∠BAD = ∠D = 90^{\circ}$。
∵ $AD // MN$,
∴ $∠BMP = ∠BAD = 90^{\circ}$,$∠PNE = ∠D = 90^{\circ}$,
∴ $∠MPB + ∠MBP = 90^{\circ}$,
∴ $∠EPN = ∠MBP$。
在 $Rt△PNC$ 中,$∠PCN = 45^{\circ}$,
∴ $△PNC$ 是等腰直角三角形,
∴ $PN = CN$,
∴ $BM = CN = PN$。
在 $△BMP$ 和 $△PNE$ 中,$\left\{\begin{array}{l} ∠PBM = ∠EPN,\\ BM = PN,\\ ∠BMP = ∠PNE,\end{array}\right.$
∴ $△BMP \cong △PNE$,
∴ $PB = PE$。

(2)解:在点 $P$ 运动的过程中,$PF$ 的长度不发生变化。理由如下:
如图 2,连接 $OB$。
∵ 点 $O$ 是正方形 $ABCD$ 对角线 $AC$ 的中点,
∴ $OB ⊥ AC$,
∴ $∠AOB = 90^{\circ}$,
∴ $∠OBP + ∠BPO = 90^{\circ}$。
∵ $∠BPE = 90^{\circ}$,
∴ $∠BPO + ∠FPE = 90^{\circ}$,
∴ $∠OBP = ∠FPE$。
∵ $EF ⊥ AC$,
∴ $∠EFP = ∠AOB = 90^{\circ}$。
由
(1)得 $PB = PE$。
在 $△OBP$ 和 $△FPE$ 中,$\left\{\begin{array}{l} ∠OBP = ∠FPE,\\ ∠BOP = ∠PFE,\\ PB = EP,\end{array}\right.$
∴ $△OBP \cong △FPE(AAS)$,
∴ $OB = PF$。
∵ $AB = 2$,$△ABO$ 是等腰直角三角形,
∴ $OB = \sqrt{2}$,
∴ $PF$ 的长为 $\sqrt{2}$。

(3)解:$PC = PA + \sqrt{2}EC$。
如图 1,
∵ $∠BAC = 45^{\circ}$,
∴ $△AMP$ 是等腰直角三角形,
∴ $PA = \sqrt{2}PM$。
由
(1)知 $PM = NE$,
∴ $PA = \sqrt{2}NE$。
∵ $△PCN$ 是等腰直角三角形,
∴ $PC = \sqrt{2}NC = \sqrt{2}(NE + EC) = \sqrt{2}NE + \sqrt{2}EC = PA + \sqrt{2}EC$。
查看更多完整答案,请扫码查看


