《2025年一遍过九年级初中数学上册北师大版》

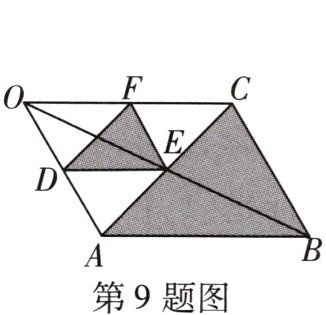
9 如图所示是利用图形的位似绘制的一幅“小鱼”图案,其中$O$为位似中心,且$OA= 2OD$,若图案中鱼身($\triangle ABC$)的面积为$S$,则鱼尾($\triangle DEF$)的面积为($\frac{1}{4}S$)

A. $\sqrt{S}$
B. $\sqrt{2}S$
C. $\frac{1}{4}S$
D. $\frac{1}{2}S$

答案： C
∵$△ABC$与$△DEF$是以O为位似中心的位似图形，$OA=2OD$，
∴$△ABC\backsim △DEF$，且相似比为$2:1$，
∴$\frac {S_{△ABC}}{S_{△DEF}}=4$，
∵$△ABC$的面积为S，
∴$△DEF$的面积为$\frac {1}{4}S$。

10 [2024渭南前进路中学期中]在如图所示的网格中,以点$O$为位似中心,四边形$ABCD$的位似图形是(A)
A. 四边形$NPMQ$
B. 四边形$NPMR$
C. 四边形$NHMQ$
D. 四边形$NHMR$

答案： A
∵ 点O为位似中心，
∴ 点A对应点N，点B对应点P，点C对应点M，点D对应点Q，
∴ 以点O为位似中心，四边形ABCD的位似图形是四边形NPMQ。

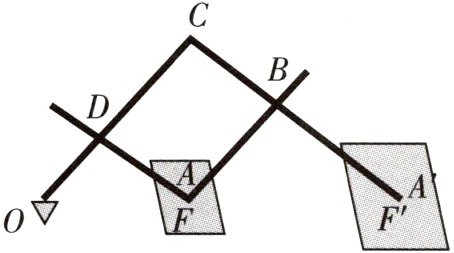
11 教材P114做一做变式[2024杭州临安区一模]如图,放缩尺是利用图形的位似将图形放大或缩小的工具,点$O$的位置固定不变,在$A$,$A'$处装有笔．当画笔$A沿图F$运动时,画笔$A'画出图形F'$,图形就放大了；反之,图形就缩小了．位似比可以通过调节点$B$,$D$的位置来确定,调整时确保$AB// DC$,$AD// BC$,点$O$,$F$,$F'$在同一直线上,若$OD:DC= 1:2$,图形$F的面积为1.5$,则图形$F'$的面积为______．

答案：
13.5 如图，因为$O$，$F$，$F'$在同一直线上，连接$OF'$，
∵$DF// CF'$，
∴$OF:FF'=OD:DC=1:2$，
∴$OF:OF'=1:3$，
∴ 图形F与图形$F'$的面积比为$1:9$，
∵ 图形F的面积为1.5，
∴ 图形$F'$的面积为13.5。

12 创新意识若$\triangle ABC绕点A逆时针旋转\alpha$后,与$\triangle ADE$构成位似图形,则我们称$\triangle ABC与\triangle ADE$互为“旋转位似图形”．
(1)知识理解
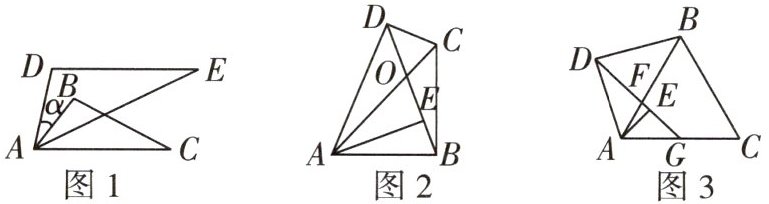
如图1,$\triangle ABC与\triangle ADE$互为“旋转位似图形”．
①若$\alpha=25^{\circ}$,$\angle D= 100^{\circ}$,$\angle C= 28^{\circ}$,则$\angle BAE= $27$^{\circ}$；
②若$AD= 6$,$DE= 7$,$AB= 4$,则$BC= $$\frac{14}{3}$．
(2)知识运用
如图2,在四边形$ABCD$中,$\angle ADC= 90^{\circ}$,$AE\perp BD于点E$,$\angle DAC= \angle DBC$,求证：$\triangle ACD与\triangle ABE$互为“旋转位似图形”．
(3)拓展提高
如图3,$\triangle ABC$为等边三角形,点$G为AC$的中点,点$F是AB$边上的一点,点$D为GF$延长线上的一点,点$E在线段GF$上,$AE\perp DG$,且$\triangle ABD与\triangle AGE$互为“旋转位似图形”．若$AB= 6$,$AD= 4$,求$\frac{DE}{GE}$的值．$\frac{2\sqrt{15}}{5}$

答案：
(1)①27
∵$△ABC$和$△ADE$互为“旋转位似图形”，
∴$△ABC\backsim △ADE$，
∴$∠D=∠B=100^{\circ }$。
∵$α=25^{\circ }$，$∠C=∠E=28^{\circ }$，
∴$∠BAE=180^{\circ }-100^{\circ }-25^{\circ }-28^{\circ }=27^{\circ }$。
②$\frac {14}{3}$
∵$△ABC\backsim △ADE$，
∴$\frac {BC}{DE}=\frac {AB}{AD}$。
∵$AD=6$，$DE=7$，$AB=4$，
∴$\frac {BC}{7}=\frac {4}{6}$，
∴$BC=\frac {14}{3}$。
(2)证明：
∵$∠DOA=∠COB$，$∠DAC=∠DBC$，
∴$△DOA\backsim △COB$，
∴$\frac {AO}{BO}=\frac {DO}{CO}$，即$\frac {AO}{DO}=\frac {BO}{CO}$，
又
∵$∠DOC=∠AOB$，
∴$△AOB\backsim △DOC$，
∴$∠DCA=∠EBA$。
∵$∠ADC=90^{\circ }$，$AE⊥BD$，
∴$∠ADC=∠AEB=90^{\circ }$，
∴$△ABE\backsim △ACD$，
∴$∠DAC=∠EAB$，
∴$△AEB$绕点A逆时针旋转$∠DAE$的度数后与$△ADC$构成位似图形，
∴$△ACD$和$△ABE$互为“旋转位似图形”。
(3)解：
∵$△ABC$为等边三角形，点G为AC的中点，
∴$AG=\frac {1}{2}AC=\frac {1}{2}AB=3$。
由题意，得$\frac {GE}{BD}=\frac {AG}{AB}=\frac {AE}{AD}=\frac {1}{2}$。
∵$AD=4$，
∴$AE=2$。
∵$AE⊥DG$，
∴$∠DEA=∠AEG=90^{\circ }$，
由勾股定理，得$GE=\sqrt {AG^{2}-AE^{2}}=\sqrt {5}$，
∴$DE=\sqrt {AD^{2}-AE^{2}}=2\sqrt {3}$，
∴$\frac {DE}{GE}=\frac {2\sqrt {3}}{\sqrt {5}}=\frac {2\sqrt {15}}{5}$。