《2025年一遍过九年级初中数学上册北师大版》

8 [2024 淄博模拟]若代数式 $ x(x - 1) $ 和 $ 3(1 - x) $ 的值互为相反数,则 $ x $ 的值为(3或1)
A. 1 或 3
B. -1 或 -3
C. 1 或 -1
D. 3 或 -3

答案： A
∵ 代数式 $x(x - 1)$ 和 $3(1 - x)$ 的值互为相反数，
∴ $x(x - 1)+3(1 - x) = 0$，
∴ $(x - 3)(x - 1) = 0$，
∴ $x - 3 = 0$ 或 $x - 1 = 0$，解得 $x = 3$ 或 $x = 1$。

9 [2024 赤峰中考]等腰三角形的两边长分别是方程 $ x^{2} - 10x + 21 = 0 $ 的两个根,则这个三角形的周长为(C)
A. 17 或 13
B. 13 或 21
C. 17
D. 13

答案： C 解方程 $x^{2}-10x + 21 = 0$，得 $x_{1}=3$，$x_{2}=7$。当等腰三角形的边长是 $3$，$3$，$7$ 时，$3 + 3\lt7$，不符合三角形的三边关系，舍去；当等腰三角形的边长是 $7$，$7$，$3$ 时，这个三角形的周长是 $7 + 7 + 3 = 17$。

若关于 $ x $ 的方程 $ x^{2} - 2px + 3q = 0 $ 的两根分别是 -3 和 5,则多项式 $ 2x^{2} - 4px + 6q $ 可以分解为$2(x + 3)(x - 5)$。

答案： $2(x + 3)(x - 5)$ 解法一 由题意，知 $x^{2}-2px + 3q=(x + 3)(x - 5)$，所以 $2x^{2}-4px + 6q = 2(x^{2}-2px + 3q)=2(x + 3)(x - 5)$。
解法二 因为方程 $x^{2}-2px + 3q = 0$ 的两根分别是 $-3$ 和 $5$，
所以 $\begin{cases}9 + 6p + 3q = 0,\\25 - 10p + 3q = 0,\end{cases}$ 解得 $\begin{cases}p = 1,\\q = -5,\end{cases}$ 所以 $2x^{2}-4px + 6q = 2x^{2}-4x - 30 = 2(x^{2}-2x - 15)=2(x + 3)(x - 5)$。

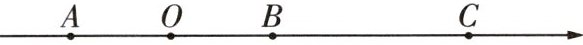
11 [2024 宜昌十六中月考]如图,已知 $ A $,$ B $,$ C $ 是数轴上异于原点 $ O $ 的三个点,且点 $ O $ 为 $ AB $ 的中点,点 $ B $ 为 $ AC $ 的中点。若点 $ B $ 表示的数是 $ x $,点 $ C $ 表示的数是 $ x^{2} - 3x $,则 $ x = $______6。

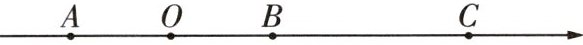
答案： 6
∵ 原点 $O$ 是 $AB$ 的中点，
∴ $OA = OB$，
∵ 点 $B$ 表示的数是 $x$，
∴ 点 $A$ 表示的数是 $-x$。
∵ 点 $B$ 是 $AC$ 的中点，
∴ $AB = BC$，即 $(x^{2}-3x)-x = x-(-x)$，整理，得 $x^{2}-6x = 0$，即 $x(x - 6) = 0$，
∴ $x_{1}=0$，$x_{2}=6$。
∵ 点 $B$ 异于原点，
∴ $x\neq0$，
∴ $x = 6$。（本题也可利用 $OC = 3OB$，列出方程求解）

12 [2025 宿迁宿豫区期中]定义新运算“⊕”如下：当 $ a \geq b $ 时,$ a⊕b = a^{2} - b^{2} $；当 $ a ＜ b $ 时,$ a⊕b = a^{2} - b $。若 $ (x - 1)⊕(2x + 1) = 0 $,则 $ x = $______$-2$ 或 $0$ 或 $4$。

答案： $-2$ 或 $0$ 或 $4$ 当 $x - 1\geq2x + 1$，即 $x\leq - 2$ 时，$(x - 1)^{2}-(2x + 1)^{2}=0$，
∴ $(x - 1 + 2x + 1)(x - 1 - 2x - 1) = 0$，即 $3x(-x - 2) = 0$，
∴ $x_{1}=0$，$x_{2}=-2$，
∵ $x\leq - 2$，
∴ $x = 0$ 舍去，只取 $x = - 2$；当 $x - 1\lt2x + 1$，即 $x\gt - 2$ 时，$(x - 1)^{2}-(2x + 1) = 0$，
∴ $x^{2}-2x + 1 - 2x - 1 = 0$，整理，得 $x(x - 4) = 0$，
∴ $x_{3}=0$，$x_{4}=4$。综上，$x$ 的值为 $-2$ 或 $0$ 或 $4$。

13 我们知道可以用公式 $ x^{2} + (p + q)x + pq = (x + p)(x + q) $ 来分解因式,解一元二次方程。
(1) $ x^{2} + 6x + 8 = 0 $ 可变形为$(x + 2)(x + 4)$= 0,$ x^{2} - 7x - 30 = 0 $ 可变形为$(x - 10)(x + 3)$= 0。
(2) 爱钻研的小明同学发现二次项系数不是 1 的方程也可以借助此方法求解。如方程 $ 3x^{2} - 7x + 2 = 0 $ 可变形为 $ (x - 2)(3x - 1) = 0 $,从而可以快速求出方程的根。

请你利用此方法尝试解方程 $ (4x + 4)(x - 3) = -7 $。

答案： 解：
(1) $(x + 2)(x + 4)$ $(x - 10)(x + 3)$
(2) 原方程可化为 $4x^{2}-8x - 5 = 0$，
可变形为 $(2x - 5)(2x + 1) = 0$，
∴ $2x - 5 = 0$ 或 $2x + 1 = 0$，
∴ $x_{1}=\frac{5}{2}$，$x_{2}=-\frac{1}{2}$。

14 [抽象能力][教材 P57T12 变式]为解方程 $ x^{4} - 5x^{2} + 4 = 0 $,我们可以将 $ x^{2} $ 视为一个整体,然后设 $ x^{2} = y $,则 $ x^{4} = y^{2} $,将原方程化为 $ y^{2} - 5y + 4 = 0 $,解这个方程得 $ y_{1} = 1 $,$ y_{2} = 4 $,所以原方程的解为 $ x_{1} = 1 $,$ x_{2} = -1 $,$ x_{3} = 2 $,$ x_{4} = -2 $。
利用上述方法解方程：
(1) $ (x^{2} - 2x)^{2} + x^{2} - 2x - 6 = 0 $；
解：设 $x^{2}-2x = t$，
原方程可化为 $t^{2}+t - 6 = 0$，
解得 $t_{1}=-3$，$t_{2}=2$。
当 $t = - 3$ 时，$x^{2}-2x = - 3$，
即 $x^{2}-2x + 3 = 0$，此方程无实数根；
当 $t = 2$ 时，$x^{2}-2x = 2$，此方程可化为 $x^{2}-2x + 1 = 3$，即 $(x - 1)^{2}=3$，两边开平方，得 $x - 1=\pm\sqrt{3}$，
所以 $x_{1}=1+\sqrt{3}$，$x_{2}=1-\sqrt{3}$，
所以原方程的解为 $x_{1}=$$1+\sqrt{3}$，$x_{2}=$$1-\sqrt{3}$。
(2) $ \frac{1}{2}(x^{2} + 4x)^{2} - x^{2} - 4x - \frac{15}{2} = 0 $。
解：令 $x^{2}+4x = y$，
原方程可化为 $y^{2}-2y - 15 = 0$，
解得 $y_{1}=-3$，$y_{2}=5$。
当 $y = - 3$ 时，$x^{2}+4x = - 3$，解得 $x=$$-1$或$-3$；
当 $y = 5$ 时，$x^{2}+4x = 5$，解得 $x=$$-5$或$1$。
所以原方程的解为 $x_{1}=$$-1$，$x_{2}=$$-3$，$x_{3}=$$-5$，$x_{4}=$$1$。

答案： 解：
(1) 设 $x^{2}-2x = t$，
原方程可化为 $t^{2}+t - 6 = 0$，
解得 $t_{1}=-3$，$t_{2}=2$。
当 $t = - 3$ 时，$x^{2}-2x = - 3$，
即 $x^{2}-2x + 3 = 0$，此方程无实数根；
当 $t = 2$ 时，$x^{2}-2x = 2$，此方程可化为 $x^{2}-2x + 1 = 3$，即 $(x - 1)^{2}=3$，两边开平方，得 $x - 1=\pm\sqrt{3}$，
所以 $x_{1}=1+\sqrt{3}$，$x_{2}=1-\sqrt{3}$，
所以原方程的解为 $x_{1}=1+\sqrt{3}$，$x_{2}=1-\sqrt{3}$。
(2) 令 $x^{2}+4x = y$，
原方程可化为 $y^{2}-2y - 15 = 0$，
解得 $y_{1}=-3$，$y_{2}=5$。
当 $y = - 3$ 时，$x^{2}+4x = - 3$，解得 $x = - 1$ 或 $-3$；
当 $y = 5$ 时，$x^{2}+4x = 5$，解得 $x = - 5$ 或 $1$。
所以原方程的解为 $x_{1}=-1$，$x_{2}=-3$，$x_{3}=-5$，$x_{4}=1$。

【回顾与思考】
一元二次方程的不同解法各有什么特点？又体现了哪些共同特点？

答案： 【解析】：一元二次方程常见的解法有直接开平方法、配方法、公式法和因式分解法。
直接开平方法：特点是当方程能化成$x^{2}=p$（$p\geq0$）或$(mx + n)^{2}=p$（$p\geq0$）的形式时，可直接开平方求解，这种方法简单直接，计算量小，但适用范围较窄，只适用于一些特殊形式的一元二次方程。
配方法：通过配方将一元二次方程转化为完全平方式来求解。它的特点是具有通用性，所有的一元二次方程都可以用配方法求解，但配方过程相对复杂，计算量较大，需要熟练掌握完全平方公式。
公式法：是利用求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$（$a\neq0$，$b^{2}-4ac\geq0$）来求解一元二次方程。其特点是通用性强，只要确定了方程中$a$、$b$、$c$的值，代入公式即可求解，但公式的推导过程较复杂，且计算时涉及到根式运算，容易出错。
因式分解法：将方程通过因式分解化为两个一次因式乘积等于零的形式，即$A\cdot B = 0$，则$A = 0$或$B = 0$，进而求解。这种方法计算简便，当方程的一边能分解因式时，用因式分解法求解较为快捷，但并不是所有的一元二次方程都能方便地进行因式分解。
这些解法的共同特点：
都是将一元二次方程转化为一元一次方程来求解，体现了“降次”的数学思想，把高次方程问题转化为低次方程问题来解决。
最终目的都是求出一元二次方程的根，以满足方程左右两边相等。
【答案】：不同解法特点：
直接开平方法：简单直接，计算量小，但适用范围窄，适用于特殊形式方程。
配方法：具有通用性，但配方过程复杂，计算量大。
公式法：通用性强，但公式推导复杂，计算涉及根式易出错。
因式分解法：计算简便，能因式分解时求解快捷，但并非所有方程都适用。
共同特点：都体现“降次”思想，将一元二次方程转化为一元一次方程求解，目的都是求出方程的根。