《2025年一遍过九年级初中数学上册北师大版》

1 [2024 内江中考]已知$\triangle ABC与\triangle DEF$相似,且相似比为$1:3$,则$\triangle ABC与\triangle DEF$的周长之比是(B)
A.$1:1$
B.$1:3$
C.$1:6$
D.$1:9$

答案： B

如果两个相似三角形的周长之比是$4:9$,其中小三角形一边上的高为 12 厘米,那么大三角形对应边上的高为27厘米.

答案： 27 设大三角形对应边上的高为 $ x $ 厘米，根据题意，得 $ \frac{12}{x} = \frac{4}{9} $，解得 $ x = 27 $。

3 [2024 西安碑林区期中]如果两个相似三角形的最长边的长分别是 35 cm 和 14 cm,它们的周长之差为 60 cm,那么这两个三角形的周长之和是______cm.
140

答案： 140 设小三角形的周长是 $ x $ 厘米，则大三角形的周长是 $ (x + 60) $ cm。根据题意，得 $ \frac{x + 60}{x} = \frac{35}{14} $，解得 $ x = 40 $，$ \therefore x + 60 = 40 + 60 = 100 $，$ \therefore $ 这两个三角形的周长之和为 $ 40 + 100 = 140 $ (cm)。

4 如图,已知矩形$ABCD的一条边AD = 8$,将矩形$ABCD$折叠,使得顶点$B落在CD边上的点P$处,折痕与边$BC交于点O$.
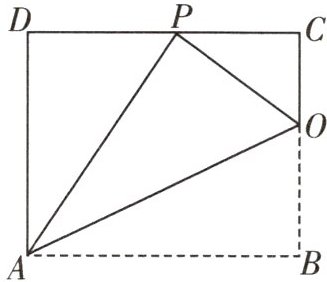
(1) 求证：$\triangle OCP \backsim \triangle PDA$.
(2) 若$\triangle OCP与\triangle PDA的周长比为1:2$,求边$AB$的长.10

答案：
(1) 证明：$ \because $ 四边形 $ ABCD $ 是矩形，
$ \therefore \angle B = \angle C = \angle D = 90^{\circ} $。
由折叠的性质可得 $ AP = AB $，$ PO = BO $，$ \angle APO = \angle B = 90^{\circ} $，
$ \therefore \angle APD = 90^{\circ} - \angle CPO = \angle POC $。
$ \because \angle C = \angle D $，$ \angle POC = \angle APD $，
$ \therefore \triangle OCP \backsim \triangle PDA $。
(2) 解：$ \because \triangle OCP \backsim \triangle PDA $，$ \triangle OCP $ 与 $ \triangle PDA $ 的周长比为 $ 1:2 $，
$ \therefore \frac{OP}{PA} = \frac{CP}{DA} = \frac{1}{2} $，$ \therefore PA = 2OP $，$ DA = 2CP $。
在矩形 $ ABCD $ 中，$ AD = 8 $，$ \therefore CP = 4 $，$ BC = 8 $。
设 $ OP = x $，则 $ OB = x $，$ CO = 8 - x $。
在 $ \text{Rt} \triangle PCO $ 中，$ \angle C = 90^{\circ} $，$ CP = 4 $，$ OP = x $，$ CO = 8 - x $，
根据勾股定理，得 $ x^{2} = (8 - x)^{2} + 4^{2} $，解得 $ x = 5 $，
$ \therefore AB = AP = 2OP = 10 $，即边 $ AB $ 的长为 10。

5 [2024 重庆中考]若两个相似三角形的相似比是$1:3$,则这两个相似三角形的面积比是(D)
A.$1:3$
B.$1:4$
C.$1:6$
D.$1:9$

答案： D

6 [2024 辽宁中考]如图,$AB // CD$,$AD与BC相交于点O$,且$\triangle AOB与\triangle DOC的面积比是1:4$,若$AB = 6$,则$CD$的长为______12.

答案： 12 $ \because AB // CD $，$ \therefore \angle A = \angle D $，$ \angle B = \angle C $，$ \therefore \triangle AOB \backsim \triangle DOC $，$ \therefore \frac{S_{\triangle AOB}}{S_{\triangle DOC}} = (\frac{AB}{DC})^{2} = \frac{1}{4} $，$ \therefore \frac{AB}{DC} = \frac{1}{2} $，$ \because AB = 6 $，$ \therefore \frac{6}{DC} = \frac{1}{2} $，$ \therefore DC = 12 $。

7 教材 P110 例 2 变式 [2025 泉州期中]如图,$\triangle ABC$的面积为 16,$D为BC$上一点,将$\triangle ABC沿AD$方向平移,使$A的对应点A'满足AA' = \frac{1}{3}DA'$,则平移前后两三角形重叠部分的面积是______.

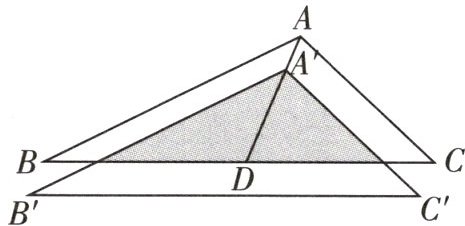
答案：
9 如图，设 $ BC $ 与 $ A'B' $ 相交于点 $ E $，$ BC $ 与 $ A'C' $ 相交于点 $ F $，$ \because AA' = \frac{1}{3}DA' $，$ \therefore \frac{DA'}{DA} = \frac{3}{4} $，由平移得 $ AB // A'B' $，$ \therefore \angle B = \angle A'ED $，$ \angle BAD = \angle EA'D $，$ \therefore \triangle ABD \backsim \triangle A'ED $，$ \therefore \frac{S_{\triangle A'ED}}{S_{\triangle ABD}} = (\frac{DA'}{DA})^{2} = \frac{9}{16} $，$ \therefore S_{\triangle A'ED} = \frac{9}{16}S_{\triangle ABD} $，同理可得 $ S_{\triangle A'DF} = \frac{9}{16}S_{\triangle ADC} $，
$ \therefore S_{\triangle A'EF} = S_{\triangle A'ED} + S_{\triangle A'DF} = \frac{9}{16}S_{\triangle ABD} + \frac{9}{16}S_{\triangle ADC} = \frac{9}{16}S_{\triangle ABC} = \frac{9}{16} \times 16 = 9 $，$ \therefore $ 平移前后两三角形重叠部分的面积是 9。

8 如图,在$□ ABCD$中,$AE:EB = 1:2$.
(1) 求$\triangle AEF与\triangle CDF$的周长比；1:3
(2) 如果$S_{\triangle AEF} = 6cm^{2}$,求$S_{\triangle CDF}$54cm²和$S_{\triangle ADF}$18cm².

答案： 解：
(1) $ \because AE:EB = 1:2 $，$ \therefore AE:AB = 1:3 $。
$ \because $ 四边形 $ ABCD $ 是平行四边形，
$ \therefore AB = CD $，$ AB // CD $，易得 $ \triangle AEF \backsim \triangle CDF $，
$ \therefore C_{\triangle AEF}:C_{\triangle CDF} = AE:CD = AE:AB = 1:3 $，
即 $ \triangle AEF $ 与 $ \triangle CDF $ 的周长比为 $ 1:3 $。
(2) $ \because \triangle AEF \backsim \triangle CDF $，
$ \therefore \frac{S_{\triangle AEF}}{S_{\triangle CDF}} = (\frac{AE}{CD})^{2} $，$ \therefore \frac{6}{S_{\triangle CDF}} = (\frac{1}{3})^{2} $，
$ \therefore S_{\triangle CDF} = 6 \times 9 = 54 $ ($ \text{cm}^{2} $)。
$ \because \triangle AEF \backsim \triangle CDF $，
$ \therefore \frac{EF}{DF} = \frac{AE}{CD} = \frac{1}{3} $，$ \therefore \frac{S_{\triangle AEF}}{S_{\triangle ADF}} = \frac{EF}{DF} = \frac{1}{3} $，
$ \therefore S_{\triangle ADF} = 3S_{\triangle AEF} = 3 \times 6 = 18 $ ($ \text{cm}^{2} $)。