《2025年一遍过九年级初中数学上册北师大版》

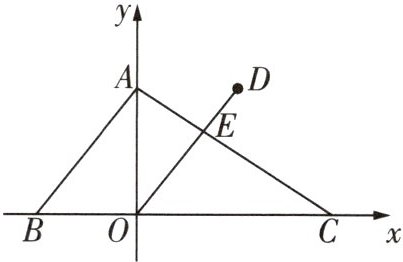
1 [2024成都石室天府中学月考]如图,△ABC的顶点A在y轴上,B,C两点都在x轴上,将边AB向右平移,平移后点A的对应点为D,点B的对应点为坐标原点O,线段DO交AC于点E(2,$\frac{8}{3}$),若AB= 5,则点D的坐标为____。

答案：
(3,4) 如图,过点D作DF⊥BC,垂足为点F,过点E作EG⊥BC,垂足为点G,
∴∠OGE=∠OFD=90°.
∵E(2, $\frac{8}{3}$),
∴OG=2,GE=$\frac{8}{3}$.
∵∠EOG=∠DOF,∠OGE=∠OFD=90°,
∴△EOG∽△DOF,
∴$\frac{EG}{DF}=\frac{OG}{OF}$.根据平移的性质可知OD=AB=5,设点D的坐标为(x,y),则OF=x,DF=y,
∴$\frac{\frac{8}{3}}{y}=\frac{2}{x}$,
∴y=$\frac{4}{3}x$.在Rt△ODF中, $OD^{2}=DF^{2}+OF^{2}$,即$5^{2}=(\frac{4}{3}x)^{2}+x^{2}$,
∴x=3或x=-3(舍去),
∴DF=y=$\frac{4}{3}\times3=4$,故点D的坐标为(3,4).

2 [2025上海金山区月考]如图,已知：点D在△ABC的边AB上,连接CD,点E在线段CD上,且∠BAE= ∠ACD= ∠B。
(1)求证：$\frac{AD}{BC}= \frac{DE}{AC}$。
证明:∵∠ACD=∠B=∠BAE,∠BAC=∠BAE+∠CAE,∠AED=∠ACD+∠CAE,∴∠AED=∠BAC,又∵∠DAE=∠B,∴△AED∽△BAC,∴$\frac{AD}{BC}=\frac{DE}{AC}$.
(2)当E为CD的中点时,求证：$\frac{AE^{2}}{CE^{2}}= \frac{AB}{AD}$。
证明:∵∠ADE=∠CDA,∠DAE=∠ACD,∴△DAE∽△DCA,∴$\frac{AE}{AC}=\frac{DE}{AD}$.∵DE=EC,∴$\frac{AE}{CE}=\frac{AC}{AD}$,∴$\frac{AE^{2}}{CE^{2}}=\frac{AC^{2}}{AD^{2}}$.∵∠DAC=∠BAC,∠ACD=∠B,∴△ACD∽△ABC,∴$\frac{AC}{AB}=\frac{AD}{AC}$,∴$AC^{2}=AD\cdot AB$,∴$\frac{AE^{2}}{CE^{2}}=\frac{AB}{AD}$.

答案： 证明:
(1)
∵∠ACD=∠B=∠BAE,∠BAC=∠BAE+∠CAE,∠AED=∠ACD+∠CAE,
∴∠AED=∠BAC,又
∵∠DAE=∠B,
∴△AED∽△BAC,
∴$\frac{AD}{BC}=\frac{DE}{AC}$.
(2)
∵∠ADE=∠CDA,∠DAE=∠ACD,
∴△DAE∽△DCA,
∴$\frac{AE}{AC}=\frac{DE}{AD}$.
∵DE=EC,
∴$\frac{AE}{CE}=\frac{AC}{AD}$,
∴$\frac{AE^{2}}{CE^{2}}=\frac{AC^{2}}{AD^{2}}$.
∵∠DAC=∠BAC,∠ACD=∠B,
∴△ACD∽△ABC,
∴$\frac{AC}{AB}=\frac{AD}{AC}$,
∴$AC^{2}=AD\cdot AB$,
∴$\frac{AE^{2}}{CE^{2}}=\frac{AB}{AD}$.

3 一题多解 学习《图形的相似》后,我们可以借助探索两个直角三角形全等的条件所获得的经验,继续探索两个直角三角形相似的条件。
(1)“对于两个直角三角形,满足一边一锐角(在两个三角形中,已知边都是该已知锐角的对边或邻边)对应相等,或两直角边对应相等,两个直角三角形全等”。类似地,你可以得到：“满足一个锐角对应相等或两直角边对应成比例,两个直角三角形相似”。
(2)“满足斜边和一条直角边对应相等的两个直角三角形全等”,类似地,你可以得到：“满足斜边和一条直角边对应成比例的两个直角三角形相似”。
请结合下列所给图形,写出已知,并完成证明过程。
已知：如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°, $\frac{AB}{A'B'}=\frac{AC}{A'C'}$。
求证：Rt△ABC∽Rt△A'B'C'。

答案： 解:
(1)一个锐角对应相等 两直角边对应成比例
(2)斜边和一条直角边对应成比例
在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°, $\frac{AB}{A'B'}=\frac{AC}{A'C'}$
证明过程如下:
解法一 设$\frac{AB}{A'B'}=\frac{AC}{A'C'}=k(k＞0)$,则AB=kA'B',AC=kA'C'.
在Rt△ABC和Rt△A'B'C'中,$\frac{BC}{B'C'}=\frac{\sqrt{AB^{2}-AC^{2}}}{\sqrt{A'B'^{2}-A'C'^{2}}}=\frac{\sqrt{k^{2}A'B'^{2}-k^{2}A'C'^{2}}}{\sqrt{A'B'^{2}-A'C'^{2}}}=k$.
∴$\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}$,
∴Rt△ABC∽Rt△A'B'C'.
解法二 在AB上截取AB''=A'B',过B''作B''C''⊥AC,垂足为C''.
∵∠C=∠B''C''A=90°,
∴B''C''//BC,
易得Rt△AB''C''∽Rt△ABC,
∴$\frac{AC}{AC''}=\frac{AB}{AB''}$.
∵AB''=A'B',
∴$\frac{AC}{AC''}=\frac{AB}{A'B'}$,
又
∵$\frac{AC}{A'C'}=\frac{AB}{A'B'}$,
∴A'C'=AC''.
在Rt△A'B'C'和Rt△AB''C''中,$\begin{cases}A'B'=AB''\\A'C'=AC''\end{cases}$,
∴Rt△A'B'C'≌Rt△AB''C'',
∴Rt△ABC∽Rt△A'B'C'.