第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
9 [2024呼伦贝尔中考]如图,边长为2的正方形ABCD的对角线AC与BD相交于点O,E是BC边上一点,F是BD上一点,连接DE,EF.若$\triangle DEF与\triangle DEC$关于直线DE对称,则$\triangle BEF$的周长是 (
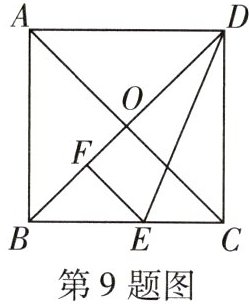
A.$2\sqrt {2}$
B.$2+\sqrt {2}$
C.$4-2\sqrt {2}$
D.$\sqrt {2}$
2√2
)
A.$2\sqrt {2}$
B.$2+\sqrt {2}$
C.$4-2\sqrt {2}$
D.$\sqrt {2}$
答案:
A
∵正方形ABCD的边长是2,
∴BD = √(CD² + CB²) = 2√2。
∵△DEF与△DEC关于直线DE对称,
∴DC = DF = 2,EC = EF,
∴△BEF的周长为BF + BE + EF = BF + BE + EC = BF + BC = BF + CD = BF + DF = BD = 2√2。
∵正方形ABCD的边长是2,
∴BD = √(CD² + CB²) = 2√2。
∵△DEF与△DEC关于直线DE对称,
∴DC = DF = 2,EC = EF,
∴△BEF的周长为BF + BE + EF = BF + BE + EC = BF + BC = BF + CD = BF + DF = BD = 2√2。
10 [2024九江期中]如图,正方形ABCD的对角线相交于点O,点E为AB上一动点.连接OE,作$OF⊥OE$交BC于点F,已知$AB= 2$,则四边形EBFO的面积为 (
A.1
B.2
C.$\sqrt {2}$
D.4
1
)A.1
B.2
C.$\sqrt {2}$
D.4
答案:
A
∵四边形ABCD是正方形,AB = 2,
∴AB = BC = 2,AC⊥BD,∠ABO = ∠BCO = 45°,OB = OC。
∵AC⊥BD,
∴∠BOC = 90°,
∴∠COF + ∠BOF = 90°。
∵OF⊥OE,
∴∠BOE + ∠BOF = 90°,
∴∠BOE = ∠COF。在△BOE和△COF中,{∠BOE = ∠COF,OB = OC,∠OBE = ∠OCF},
∴△BOE≌△COF(ASA),
∴S△BOE = S△COF,
∴S四边形EBFO = S△COF + S△BOF = S△BOC,
∵AB = BC = 2,
∴S正方形ABCD = 4,
∴S△BOC = 1/4S正方形ABCD = 1,
∴四边形EBFO的面积为1。
∵四边形ABCD是正方形,AB = 2,
∴AB = BC = 2,AC⊥BD,∠ABO = ∠BCO = 45°,OB = OC。
∵AC⊥BD,
∴∠BOC = 90°,
∴∠COF + ∠BOF = 90°。
∵OF⊥OE,
∴∠BOE + ∠BOF = 90°,
∴∠BOE = ∠COF。在△BOE和△COF中,{∠BOE = ∠COF,OB = OC,∠OBE = ∠OCF},
∴△BOE≌△COF(ASA),
∴S△BOE = S△COF,
∴S四边形EBFO = S△COF + S△BOF = S△BOC,
∵AB = BC = 2,
∴S正方形ABCD = 4,
∴S△BOC = 1/4S正方形ABCD = 1,
∴四边形EBFO的面积为1。
11 [2023枣庄中考]如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,$CE= 7$,F为DE的中点,若$\triangle CEF$的周长为32,则OF的长为______
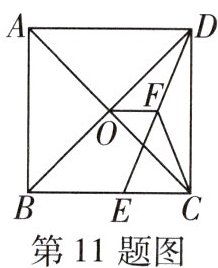
17/2
.
答案:
17/2
∵四边形ABCD是正方形,
∴OB = OD,∠BCD = 90°,
∵F为DE的中点,
∴CF = EF = DF。
∵△CEF的周长为32,
∴CF + EF + CE = 32,
∵CE = 7,
∴CF + EF = 25,
∴DF + EF = 25,即DE = 25。在Rt△CDE中,根据勾股定理可得CD = 24,
∴BC = 24,
∴BE = 24 - 7 = 17。
∵O,F分别为BD,DE的中点,
∴OF为△BDE的中位线,
∴OF = 1/2BE = 17/2。
∵四边形ABCD是正方形,
∴OB = OD,∠BCD = 90°,
∵F为DE的中点,
∴CF = EF = DF。
∵△CEF的周长为32,
∴CF + EF + CE = 32,
∵CE = 7,
∴CF + EF = 25,
∴DF + EF = 25,即DE = 25。在Rt△CDE中,根据勾股定理可得CD = 24,
∴BC = 24,
∴BE = 24 - 7 = 17。
∵O,F分别为BD,DE的中点,
∴OF为△BDE的中位线,
∴OF = 1/2BE = 17/2。
12 [2025深圳罗湖区期中]如图,已知E,F分别是正方形ABCD的边AB,BC上的点,且DE,DF分别与对角线AC相交于M,N,若$∠EDF= 40^{\circ }$,则$∠BME+∠BNF= $______$^{\circ }$.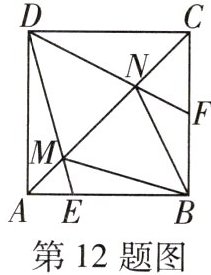

答案:
80 连接BD,如图,
∵四边形ABCD是正方形,AC为对角线,
∴AB = BC = CD = AD,∠BAC = ∠DAC = ∠BCA = ∠DCA = 45°。在△AMB和△AMD中,{AB = AD,∠BAM = ∠DAM,AM = AM},
∴△AMB≌△AMD(SAS),
∴MB = MD,
∴∠MBD = ∠MDB,
∴∠BME = ∠MBD + ∠MDB = 2∠MDB。同理△BCN≌△DCN(SAS),
∴NB = ND,
∴∠NBD = ∠NDB,
∴∠BNF = ∠NBD + ∠NDB = 2∠NDB,
∴∠BME + ∠BNF = 2(∠MDB + ∠NDB) = 2∠EDF = 80°。

80 连接BD,如图,
∵四边形ABCD是正方形,AC为对角线,
∴AB = BC = CD = AD,∠BAC = ∠DAC = ∠BCA = ∠DCA = 45°。在△AMB和△AMD中,{AB = AD,∠BAM = ∠DAM,AM = AM},
∴△AMB≌△AMD(SAS),
∴MB = MD,
∴∠MBD = ∠MDB,
∴∠BME = ∠MBD + ∠MDB = 2∠MDB。同理△BCN≌△DCN(SAS),
∴NB = ND,
∴∠NBD = ∠NDB,
∴∠BNF = ∠NBD + ∠NDB = 2∠NDB,
∴∠BME + ∠BNF = 2(∠MDB + ∠NDB) = 2∠EDF = 80°。

13 教材P22 T2变式[2025深圳坪山区期中]如图,在正方形ABCD中,点F是边AB上一点,连接DF,点E为DF的中点.连接BE,CE,AE.
(1)求证:$∠DAE= ∠ADE$.
(2)求证:$\triangle AEB\cong \triangle DEC$.
(3)当$EB= BC$时,$∠AFD$的度数为______
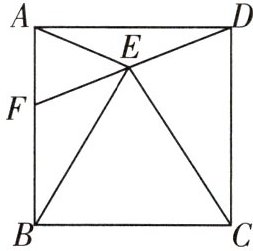
(1)求证:$∠DAE= ∠ADE$.
(2)求证:$\triangle AEB\cong \triangle DEC$.
(3)当$EB= BC$时,$∠AFD$的度数为______
75°
.
答案:
(1)证明:
∵四边形ABCD是正方形,
∴∠BAD = 90°。
∵点E为DF的中点,
∴AE = EF = DE = 1/2DF,
∴∠EAD = ∠EDA。
(2)证明:
∵四边形ABCD是正方形,
∴AB = DC,∠BAD = ∠ADC = 90°。
∵∠EAD = ∠EDA,∠BAE = ∠BAD - ∠EAD,∠CDE = ∠ADC - ∠EDA,
∴∠BAE = ∠CDE。在△AEB和△DEC中,{AB = DC,∠BAE = ∠CDE,AE = DE},
∴△AEB≌△DEC(SAS)。
(3)75°
∵△AEB≌△DEC,
∴EB = EC。
∵EB = BC,
∴EB = BC = EC,
∴△BCE是等边三角形,
∴∠EBC = 60°,
∴∠ABE = 90° - 60° = 30°。
∵EB = BC = AB,
∴∠BAE = 1/2(180° - 30°) = 75°。
∵AE = EF,
∴∠AFD = ∠BAE = 75°。
∵四边形ABCD是正方形,
∴∠BAD = 90°。
∵点E为DF的中点,
∴AE = EF = DE = 1/2DF,
∴∠EAD = ∠EDA。
(2)证明:
∵四边形ABCD是正方形,
∴AB = DC,∠BAD = ∠ADC = 90°。
∵∠EAD = ∠EDA,∠BAE = ∠BAD - ∠EAD,∠CDE = ∠ADC - ∠EDA,
∴∠BAE = ∠CDE。在△AEB和△DEC中,{AB = DC,∠BAE = ∠CDE,AE = DE},
∴△AEB≌△DEC(SAS)。
(3)75°
∵△AEB≌△DEC,
∴EB = EC。
∵EB = BC,
∴EB = BC = EC,
∴△BCE是等边三角形,
∴∠EBC = 60°,
∴∠ABE = 90° - 60° = 30°。
∵EB = BC = AB,
∴∠BAE = 1/2(180° - 30°) = 75°。
∵AE = EF,
∴∠AFD = ∠BAE = 75°。
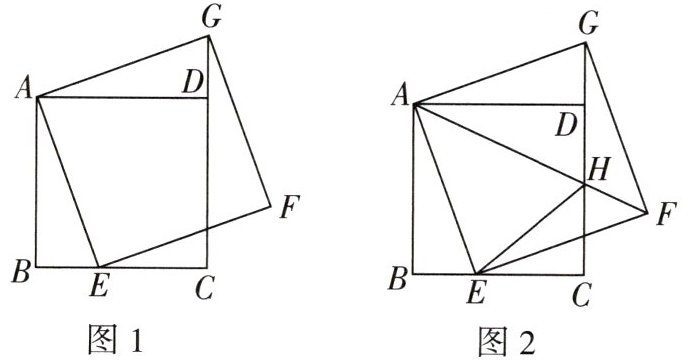
14 [2025昆明期末]如图1,四边形ABCD是正方形,点E是BC上一点,连接AE,以AE为一边作正方形AEFG,连接DG.
(1)求证:$∠ADG= 90^{\circ }$.
证明:∵四边形ABCD和四边形AEFG都是正方形,∴AB = AD,AE = AG,∠DAB = ∠B = ∠EAG = 90°,∴∠EAD + ∠DAG = 90°,∠BAE + ∠EAD = 90°,∴∠BAE = ∠DAG,在△BAE和△DAG中,{AE = AG,∠BAE = ∠DAG,AB = AD},∴△BAE≌△DAG(SAS),∴∠ADG = ∠B = 90°。
(2)如图2,连接AF交CD于点H,连接EH,请探究EH,BE,DH三条线段之间的数量关系,并说明理由.
解:EH,BE,DH三条线段之间的数量关系为
(1)求证:$∠ADG= 90^{\circ }$.
证明:∵四边形ABCD和四边形AEFG都是正方形,∴AB = AD,AE = AG,∠DAB = ∠B = ∠EAG = 90°,∴∠EAD + ∠DAG = 90°,∠BAE + ∠EAD = 90°,∴∠BAE = ∠DAG,在△BAE和△DAG中,{AE = AG,∠BAE = ∠DAG,AB = AD},∴△BAE≌△DAG(SAS),∴∠ADG = ∠B = 90°。
(2)如图2,连接AF交CD于点H,连接EH,请探究EH,BE,DH三条线段之间的数量关系,并说明理由.
解:EH,BE,DH三条线段之间的数量关系为
BE + DH = EH
。理由如下:由(1)得△BAE≌△DAG,∴BE = DG,AE = AG,∵四边形AEFG是正方形,∴∠EAH = ∠GAH = 45°,在△EAH和△GAH中,{AE = AG,∠EAH = ∠GAH,AH = AH},∴△EAH≌△GAH(SAS),∴EH = GH,又∵DG + DH = GH,∴BE + DH = EH。
答案:
(1)证明:
∵四边形ABCD和四边形AEFG都是正方形,
∴AB = AD,AE = AG,∠DAB = ∠B = ∠EAG = 90°,
∴∠EAD + ∠DAG = 90°,∠BAE + ∠EAD = 90°,
∴∠BAE = ∠DAG,在△BAE和△DAG中,{AE = AG,∠BAE = ∠DAG,AB = AD},
∴△BAE≌△DAG(SAS),
∴∠ADG = ∠B = 90°。
(2)解:BE + DH = EH。理由如下:由(1)得△BAE≌△DAG,
∴BE = DG,AE = AG,
∵四边形AEFG是正方形,
∴∠EAH = ∠GAH = 45°,在△EAH和△GAH中,{AE = AG,∠EAH = ∠GAH,AH = AH},
∴△EAH≌△GAH(SAS),
∴EH = GH,又
∵DG + DH = GH,
∴BE + DH = EH。
∵四边形ABCD和四边形AEFG都是正方形,
∴AB = AD,AE = AG,∠DAB = ∠B = ∠EAG = 90°,
∴∠EAD + ∠DAG = 90°,∠BAE + ∠EAD = 90°,
∴∠BAE = ∠DAG,在△BAE和△DAG中,{AE = AG,∠BAE = ∠DAG,AB = AD},
∴△BAE≌△DAG(SAS),
∴∠ADG = ∠B = 90°。
(2)解:BE + DH = EH。理由如下:由(1)得△BAE≌△DAG,
∴BE = DG,AE = AG,
∵四边形AEFG是正方形,
∴∠EAH = ∠GAH = 45°,在△EAH和△GAH中,{AE = AG,∠EAH = ∠GAH,AH = AH},
∴△EAH≌△GAH(SAS),
∴EH = GH,又
∵DG + DH = GH,
∴BE + DH = EH。
查看更多完整答案,请扫码查看


