《2025年一遍过九年级初中数学上册北师大版》

1 [2024运城期中]要使平行四边形ABCD成为菱形,还需添加的条件是 (B)
A. $ AB = CD $
B. $ AB = BC $
C. $ AD = BC $
D. $ AC = BD $

答案： B

2 [2024抚州期中]若菱形ABCD的周长是40,则它的边长为 (10)
A. 20
B. 10
C. 15
D. 25

答案： B
∵ 四边形 ABCD 是菱形，
∴ $ AB = BC = CD = AD $（菱形的四条边相等）。又
∵ 菱形 ABCD 的周长为 40，
∴ $ AB = BC = CD = AD = 10 $。

3 [2025保定月考]如图,下列直线是菱形的对称轴的是 (C)

A. $ l_{1} $
B. $ l_{2} 和 l_{4} $
C. $ l_{1} 和 l_{3} $
D. 全部都是

答案： C

4 [2023湘潭中考]如图,菱形ABCD中,连接AC,BD,若$ ∠1 = 20^{\circ} $,则$ ∠2 $的度数为 (C)
A. $ 20^{\circ} $
B. $ 60^{\circ} $
C. $ 70^{\circ} $
D. $ 80^{\circ} $

答案： C 设 AC，BD 交于点 O，
∵ 四边形 ABCD 是菱形，
∴ $ AB // CD $，$ AC \perp BD $，
∴ $ \angle DCA = \angle 1 = 20^{\circ} $，$ \angle COD = 90^{\circ} $，
∴ $ \angle 2 = 90^{\circ} - \angle DCA = 70^{\circ} $。

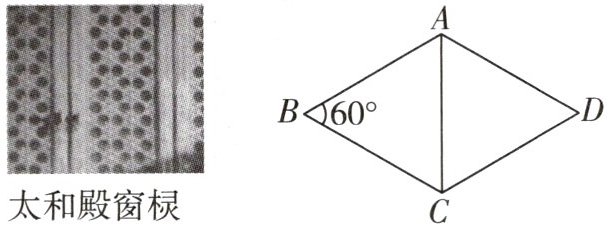
5 新情境[2025兰州期中]小明在参观故宫博物院时,被太和殿窗棂上的三交六椀菱花图案所吸引,他从中提取出一个含$ 60^{\circ} $角的菱形ABCD(如图所示),若边AB的长度为a,则对角线AC的长度为 (B)

A. 2a
B. a
C. $ \sqrt{3}a $
D. $ \frac{1}{2}a $

答案： B 由题意可知 $ AB = BC = a $，结合 $ \angle B = 60^{\circ} $，可得 $ \triangle ABC $ 是等边三角形，所以 $ AC = AB = a $。

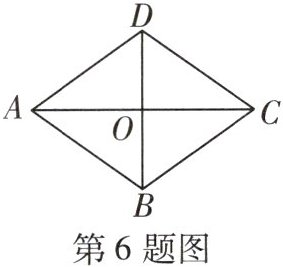
6 教材P4随堂练习变式[2024佛山禅城区月考]如图,菱形ABCD中,$ AC = 8 $,$ AD = 5 $,则$ BD = $ (6)

A. 3
B. 4
C. 6
D. 10

答案： C
∵ $ AC = 8 $，四边形 ABCD 是菱形，
∴ $ AO = CO = 4 $，$ BO = DO $，$ AC \perp BD $，
∴ $ OD = \sqrt{AD^{2} - OA^{2}} = \sqrt{5^{2} - 4^{2}} = 3 $，
∴ $ BD = 2OD = 2 × 3 = 6 $。
方法指导
求解菱形中的线段长的方法
菱形的对角线互相垂直，计算菱形中的线段长时，通常结合勾股定理进行求解。

7 [2025南宁青秀区月考]如图,菱形菜圃ABCD中,$ AB = 8m $,对角线AC,BD交于点O,从点O处拉一根水管至CD的中点E,则水管OE的长度为 (4m)
A. 2m
B. 4m
C. 8m
D. 16m

答案： B
∵ 四边形 ABCD 是菱形，
∴ $ DO = OB $，$ AB = BC = 8m $。
∵ E 是 CD 的中点，
∴ OE 是 $ \triangle BCD $ 的中位线，
∴ $ OE = \frac{1}{2}BC = 4m $。

8 [2024济南中考]如图,在菱形ABCD中,$ AE ⊥ CD $,垂足为E,$ CF ⊥ AD $,垂足为F. 求证:$ AF = CE $.

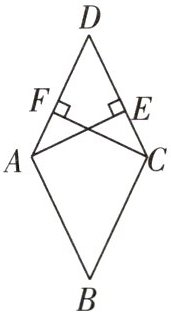
证明：∵ 四边形 ABCD 是菱形，∴ $ AD = CD $。∵ $ AE \perp CD $，$ CF \perp AD $，∴ $ \angle AED = \angle CFD = 90^{\circ} $。
在 $ \triangle AED $ 和 $ \triangle CFD $ 中，$ \begin{cases} \angle AED = \angle CFD \\ \angle D = \angle D \\ AD = CD \end{cases} $，∴ $ \triangle AED \cong \triangle CFD ( AAS ) $，∴ $ DE = DF $，∴ $ AD - DF = CD - DE $，∴ $ AF = CE $。

答案： 证明：
∵ 四边形 ABCD 是菱形，
∴ $ AD = CD $。
∵ $ AE \perp CD $，$ CF \perp AD $，
∴ $ \angle AED = \angle CFD = 90^{\circ} $。
在 $ \triangle AED $ 和 $ \triangle CFD $ 中，$ \begin{cases} \angle AED = \angle CFD \\ \angle D = \angle D \\ AD = CD \end{cases} $，
∴ $ \triangle AED \cong \triangle CFD ( AAS ) $，
∴ $ DE = DF $，
∴ $ AD - DF = CD - DE $，
∴ $ AF = CE $。