《2025年一遍过九年级初中数学上册北师大版》

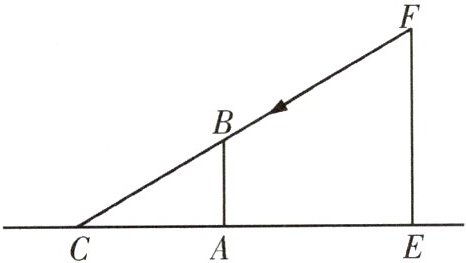
7 如图,一根直立于水平地面的木杆AB在灯光下形成影子AC($AC＞AB$),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知$AE= 5m$,在旋转过程中,影长的最大值为5m,最小值为3m,且影长最长时,木杆与光线垂直,求路灯EF的高度.

答案：
解题思路:本题的难点是知道当木杆旋转到达地面时，影子最短，即最短影长等于木杆AB的长,在木杆绕点A按逆时针方向旋转的过程中，木杆AB的长度不变，为3m，影长在不断变化.
解:当木杆AB旋转到达地面时，其影子的长度最短，此时影子的长度等于木杆AB的长度,$\therefore AB=3m.$
∵影长最长时，木杆与光线垂直(如图),$\therefore AC'=5m.$

在$Rt\triangle AB'C'$中，根据勾股定理，得$B'C'=\sqrt {AC'^{2}-AB'^{2}}=\sqrt {5^{2}-3^{2}}=4(m).$
在$Rt\triangle B'C'A$和$Rt\triangle FC'E$中,$∠B'C'A=∠EC'F,∠C'B'A=∠C'EF,\therefore \triangle C'AB'\backsim \triangle C'FE,\therefore \frac {B'C'}{EC'}=\frac {B'A}{EF}.$
$\because AE=5m,\therefore EC'=AE+AC'=10m,$
$\therefore \frac {4}{10}=\frac {3}{EF},\therefore EF=7.5m,$
即路灯EF的高度为7.5m.
归纳总结
求解本题的关键是弄清楚哪些量发生变化，哪些量不发生变化.在解题过程中，利用相似三角形的性质进行求解.

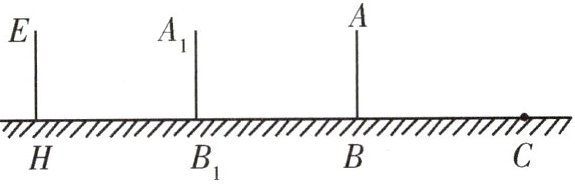
8 学习投影后,小刚、小雯利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6m的小刚(AB)的影子BC的长是3m,而小雯(EH)刚好在路灯灯泡的正下方H点,并测得$HB= 6m$.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G.
(2)求路灯灯泡的垂直高度GH.
(3)如果小刚沿BH方向向小雯(点H)走去,当小刚走到BH的中点$B_{1}$处时,求其影子$B_{1}C_{1}$的长;当小刚继续走剩下路程的$\frac{1}{3}到B_{2}$处时,求其影子$B_{2}C_{2}$的长;当小刚继续走剩下路程的$\frac{1}{4}到B_{3}$处时……按此规律继续走下去,当小刚走剩下路程的$\frac{1}{n+1}到B_{n}$处时,求其影子$B_{n}C_{n}$的长.

答案：
解:
(1)如图1所示.

(2)由题意，得$\triangle ABC\backsim \triangle GHC,$
$\therefore \frac {AB}{GH}=\frac {BC}{HC},\therefore \frac {1.6}{GH}=\frac {3}{6+3},$
$\therefore GH=4.8m.$
(3)如图2，由题意，得$\triangle A_{1}B_{1}C_{1}\backsim \triangle GHC_{1},$
$\therefore \frac {A_{1}B_{1}}{GH}=\frac {B_{1}C_{1}}{HC_{1}},$
设$B_{1}C_{1}$的长为$x m$，则$\frac {1.6}{4.8}=\frac {x}{x+3},$
$\therefore x=\frac {3}{2}$，即$B_{1}C_{1}=\frac {3}{2}m.$
同理可得$\frac {1.6}{4.8}=\frac {B_{2}C_{2}}{B_{2}C_{2}+2},\therefore B_{2}C_{2}=1m,$
$\therefore \frac {1.6}{4.8}=\frac {B_{n}C_{n}}{B_{n}C_{n}+\frac {1}{n+1}×6},\therefore B_{n}C_{n}=\frac {3}{n+1}m.$