第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
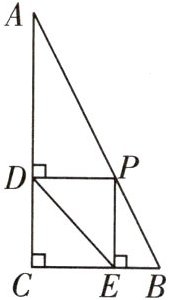
1 [2024 西藏中考]如图,在$Rt△ABC$中,$∠C= 90^{\circ },AC= 12,BC= 5$,点 P 是边 AB 上任意一点,过点 P 作$PD⊥AC,PE⊥BC$,垂足分别为点 D,E,连接 DE,则 DE 的最小值是 ( )
A.$\frac {13}{2}$
B.$\frac {60}{13}$
C.$\frac {12}{5}$
D.$\frac {30}{13}$

A.$\frac {13}{2}$
B.$\frac {60}{13}$
C.$\frac {12}{5}$
D.$\frac {30}{13}$
答案:
B 如图,连接CP,作CQ⊥AB于点Q,
∵∠ACB=90°,AC=12,BC=5,
∴AB=
$\sqrt {AC^{2}+BC^{2}}=\sqrt {12^{2}+5^{2}}=13$,
∴$S_{\triangle ABC}=\frac {1}{2}\times$
13×CQ=$\frac {1}{2}\times 12\times 5$,
∴CQ=$\frac {60}{13}$,
∵PD⊥AC,
PE⊥BC,垂足分别为点D,E,
∴∠PDC=∠PEC=∠DCE=
90°,
∴四边形PECD是矩形,
∴CP=DE,
∵CP≥CQ,
∴DE≥
$\frac {60}{13}$,
∴DE的最小值为$\frac {60}{13}$。

B 如图,连接CP,作CQ⊥AB于点Q,
∵∠ACB=90°,AC=12,BC=5,
∴AB=
$\sqrt {AC^{2}+BC^{2}}=\sqrt {12^{2}+5^{2}}=13$,
∴$S_{\triangle ABC}=\frac {1}{2}\times$
13×CQ=$\frac {1}{2}\times 12\times 5$,
∴CQ=$\frac {60}{13}$,
∵PD⊥AC,
PE⊥BC,垂足分别为点D,E,
∴∠PDC=∠PEC=∠DCE=
90°,
∴四边形PECD是矩形,
∴CP=DE,
∵CP≥CQ,
∴DE≥
$\frac {60}{13}$,
∴DE的最小值为$\frac {60}{13}$。

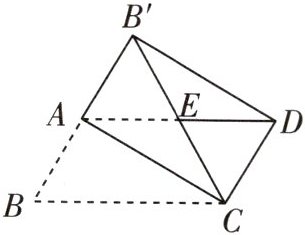
2 如图,在$□ ABCD$的纸片中,$AB⊥AC$,将$△ABC$沿对角线 AC 翻折,得到$△AB'C,B'C$与 AD 交于点 E,连接$B'D$.
(1)求证:四边形$ACDB'$为矩形.
(2)若四边形 ABCD 的面积为$12cm^{2}$,则翻折后纸片重叠部分$△ACE$的面积为____.
(1)求证:四边形$ACDB'$为矩形.
(2)若四边形 ABCD 的面积为$12cm^{2}$,则翻折后纸片重叠部分$△ACE$的面积为____.

答案:
解题思路:
(1)
四边形ABCD是平行四边形→AB//CD,AB=CD
△ABC翻折得到△AB'C,AB⊥AC→B,A,B'三点共线,AB=AB'
→AB'//CD,AB'=CD
→□ACDB'是矩形→四边形ACDB'为平行四边形
→AD=B'C
(2)
四边形ACDB'是矩形→AE=DE→$S_{\triangle ACE}=\frac {1}{2}S_{\triangle ACD}$
(1)证明:
∵四边形ABCD是平行四边形,
∴AB//CD,AB=CD。
∵△AB'C是由△ABC翻折得到的,AB⊥AC,
∴AB=AB',点A,B,B'在同一条直线上,
∴AB'//CD,AB'=CD,
∴四边形ACDB'是平行四边形。
又
∵B'C=BC=AD,
∴四边形ACDB'是矩形。
(2)3cm²
由四边形ACDB'是矩形,得AE=DE。
∵$S_{//ogram ABCD}=12cm^{2}$,
∴$S_{\triangle ACD}=6cm^{2}$,
∴$S_{\triangle AEC}=\frac {1}{2}S_{\triangle ACD}=3cm^{2}$。

解题思路:
(1)
四边形ABCD是平行四边形→AB//CD,AB=CD
△ABC翻折得到△AB'C,AB⊥AC→B,A,B'三点共线,AB=AB'
→AB'//CD,AB'=CD
→□ACDB'是矩形→四边形ACDB'为平行四边形
→AD=B'C
(2)
四边形ACDB'是矩形→AE=DE→$S_{\triangle ACE}=\frac {1}{2}S_{\triangle ACD}$
(1)证明:
∵四边形ABCD是平行四边形,
∴AB//CD,AB=CD。
∵△AB'C是由△ABC翻折得到的,AB⊥AC,
∴AB=AB',点A,B,B'在同一条直线上,
∴AB'//CD,AB'=CD,
∴四边形ACDB'是平行四边形。
又
∵B'C=BC=AD,
∴四边形ACDB'是矩形。
(2)3cm²
由四边形ACDB'是矩形,得AE=DE。
∵$S_{//ogram ABCD}=12cm^{2}$,
∴$S_{\triangle ACD}=6cm^{2}$,
∴$S_{\triangle AEC}=\frac {1}{2}S_{\triangle ACD}=3cm^{2}$。

(1)求证:四边形 ADCE 是矩形.
证明:∵AB=AC,D 是 BC 的中点,
∴AD⊥BC,即∠ADC=∠ADB=90°。
∵CE//AD,∴∠ECD=∠ADB=90°。
∵AE⊥AD,∴∠EAD=90°,
∴∠ADC=∠ECD=∠EAD=90°,
∴四边形 ADCE 是矩形。
(2)若BC= 4,CE= 3,求 EF 的长.
解:∵AB=AC,D是BC的中点,BC=4,
∴BD=CD=$\frac {1}{2}BC=2$。
由(1)可知,四边形ADCE是矩形,
∴AE=CD=2,∠AEC=90°。
在Rt△AEC中,AE=2,CE=3。
∴AC=$\sqrt {AE^{2}+CE^{2}}=\sqrt {2^{2}+3^{2}}=\sqrt {13}$。
∵EF⊥AC,∴$S_{\triangle AEC}=\frac {1}{2}AC\cdot EF=\frac {1}{2}AE\cdot CE$,
∴EF=$\frac {AE\cdot CE}{AC}=\frac {2× 3}{\sqrt {13}}=$
证明:∵AB=AC,D 是 BC 的中点,
∴AD⊥BC,即∠ADC=∠ADB=90°。
∵CE//AD,∴∠ECD=∠ADB=90°。
∵AE⊥AD,∴∠EAD=90°,
∴∠ADC=∠ECD=∠EAD=90°,
∴四边形 ADCE 是矩形。
(2)若BC= 4,CE= 3,求 EF 的长.
解:∵AB=AC,D是BC的中点,BC=4,
∴BD=CD=$\frac {1}{2}BC=2$。
由(1)可知,四边形ADCE是矩形,
∴AE=CD=2,∠AEC=90°。
在Rt△AEC中,AE=2,CE=3。
∴AC=$\sqrt {AE^{2}+CE^{2}}=\sqrt {2^{2}+3^{2}}=\sqrt {13}$。
∵EF⊥AC,∴$S_{\triangle AEC}=\frac {1}{2}AC\cdot EF=\frac {1}{2}AE\cdot CE$,
∴EF=$\frac {AE\cdot CE}{AC}=\frac {2× 3}{\sqrt {13}}=$
$\frac {6\sqrt {13}}{13}$
。
答案:
(1)证明:
∵AB=AC,D是BC的中点,
∴AD⊥BC,即∠ADC=∠ADB=90°。
∵CE//AD,
∴∠ECD=∠ADB=90°。
∵AE⊥AD,
∴∠EAD=90°,
∴∠ADC=∠ECD=∠EAD=90°,
∴四边形ADCE是矩形。
(2)解:
∵AB=AC,D是BC的中点,BC=4,
∴BD=CD=$\frac {1}{2}BC=2$。
由
(1)可知,四边形ADCE是矩形,
∴AE=CD=2,∠AEC=90°。
在Rt△AEC中,AE=2,CE=3。
∴AC=$\sqrt {AE^{2}+CE^{2}}=\sqrt {2^{2}+3^{2}}=\sqrt {13}$。
∵EF⊥AC,
∴$S_{\triangle AEC}=\frac {1}{2}AC\cdot EF=\frac {1}{2}AE\cdot CE$,
∴EF=$\frac {AE\cdot CE}{AC}=\frac {2\times 3}{\sqrt {13}}=\frac {6\sqrt {13}}{13}$。
(1)证明:
∵AB=AC,D是BC的中点,
∴AD⊥BC,即∠ADC=∠ADB=90°。
∵CE//AD,
∴∠ECD=∠ADB=90°。
∵AE⊥AD,
∴∠EAD=90°,
∴∠ADC=∠ECD=∠EAD=90°,
∴四边形ADCE是矩形。
(2)解:
∵AB=AC,D是BC的中点,BC=4,
∴BD=CD=$\frac {1}{2}BC=2$。
由
(1)可知,四边形ADCE是矩形,
∴AE=CD=2,∠AEC=90°。
在Rt△AEC中,AE=2,CE=3。
∴AC=$\sqrt {AE^{2}+CE^{2}}=\sqrt {2^{2}+3^{2}}=\sqrt {13}$。
∵EF⊥AC,
∴$S_{\triangle AEC}=\frac {1}{2}AC\cdot EF=\frac {1}{2}AE\cdot CE$,
∴EF=$\frac {AE\cdot CE}{AC}=\frac {2\times 3}{\sqrt {13}}=\frac {6\sqrt {13}}{13}$。
4 [2025 深圳红岭教育集团期中]如图,在菱形 ABCD 中,对角线 AC,BD 相交于点 O,延长 CB 到点 E,使得$BE= BC$.连接 AE,过点 B 作$BF// AC$,交 AE 于点 F,连接 OF.
(1)求证:四边形 AFBO 是矩形.
(2)若$∠E= 30^{\circ },OF= 2$,求菱形 ABCD 的面积.
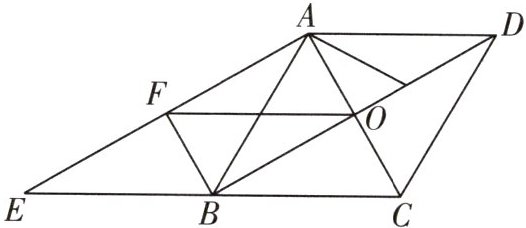
(1)求证:四边形 AFBO 是矩形.
(2)若$∠E= 30^{\circ },OF= 2$,求菱形 ABCD 的面积.
$2\sqrt{3}$

答案:
解题思路:
(1)先证四边形AEBD是平行四边形,再证
∠AOB=90°,即可得出结论。
(2)由矩形的性质得∠AFB=
90°,OF=AB=2,则∠BFE=∠FBO=90°。由∠E=∠BOF=
30°,可得BF=1,由直角三角形性质得BE=2BF=2。在
Rt△AEC中,BE=BC,由直角三角形性质得AB=BE=BC=
2,得到△ABC为等边三角形,即可求出菱形ABCD的面积。
(1)证明:
∵四边形ABCD是菱形,
∴AD//BC,AC⊥BD,AD=BC,
∵BE=BC,
∴AD=BE,
∴四边形AEBD是平行四边形,
∴AE//BD。
∵BF//AC,
∴四边形AFBO是平行四边形。
∵AC⊥BD,
∴∠AOB=90°,
∴平行四边形AFBO是矩形。
(2)解:由
(1)知四边形AFBO是矩形,
∴∠AFB=90°,OF=AB,
∴∠BFE=∠FBO=90°。
又
∵∠E=∠BOF=30°,OF=2,
∴BF=1,
∴BE=2BF=2。
在Rt△AEC中,BE=BC,
∴AB=BE=BC=2,
∴△ABC为等边三角形,
∴AC=AB=2,AO=$\frac {1}{2}AC=1$,OB=$\sqrt {AB^{2}-AO^{2}}=\sqrt {3}$,
∴$S_{菱形ABCD}=2S_{\triangle ABC}=2\times \frac {1}{2}\times 2\times \sqrt {3}=2\sqrt {3}$。
(1)先证四边形AEBD是平行四边形,再证
∠AOB=90°,即可得出结论。
(2)由矩形的性质得∠AFB=
90°,OF=AB=2,则∠BFE=∠FBO=90°。由∠E=∠BOF=
30°,可得BF=1,由直角三角形性质得BE=2BF=2。在
Rt△AEC中,BE=BC,由直角三角形性质得AB=BE=BC=
2,得到△ABC为等边三角形,即可求出菱形ABCD的面积。
(1)证明:
∵四边形ABCD是菱形,
∴AD//BC,AC⊥BD,AD=BC,
∵BE=BC,
∴AD=BE,
∴四边形AEBD是平行四边形,
∴AE//BD。
∵BF//AC,
∴四边形AFBO是平行四边形。
∵AC⊥BD,
∴∠AOB=90°,
∴平行四边形AFBO是矩形。
(2)解:由
(1)知四边形AFBO是矩形,
∴∠AFB=90°,OF=AB,
∴∠BFE=∠FBO=90°。
又
∵∠E=∠BOF=30°,OF=2,
∴BF=1,
∴BE=2BF=2。
在Rt△AEC中,BE=BC,
∴AB=BE=BC=2,
∴△ABC为等边三角形,
∴AC=AB=2,AO=$\frac {1}{2}AC=1$,OB=$\sqrt {AB^{2}-AO^{2}}=\sqrt {3}$,
∴$S_{菱形ABCD}=2S_{\triangle ABC}=2\times \frac {1}{2}\times 2\times \sqrt {3}=2\sqrt {3}$。
查看更多完整答案,请扫码查看


