《2025年一遍过九年级初中数学上册北师大版》

8 [2024达州期末]如图,在四边形ABCD中,已知$∠ADC= ∠BAC$,那么补充下列条件后不能判定$\triangle ADC和\triangle BAC$相似的是 (C)

A. CA平分$∠BCD$
B.$\frac {AD}{AB}= \frac {DC}{AC}$
C.$AC^{2}= BC\cdot CD$
D.$∠DAC= ∠ABC$

答案： C

9 如图,在等边三角形ABC中,D为AC的中点,$\frac {AE}{EB}= \frac {1}{3}$,和$\triangle AED$相似的三角形有 (C)
A. 1个
B. 2个
C. 3个
D. 4个

答案： C $\because △ABC$是等边三角形，$\therefore AB=AC=BC,∠A=∠ABC=∠C=60^{\circ }$，又$\because D$是$AC$的中点，$\therefore BD⊥AC,∠ABD=30^{\circ },\frac {AD}{AC}=\frac {1}{2},\because \frac {AE}{EB}=\frac {1}{3},\therefore \frac {AE}{AB}=\frac {1}{4},\therefore \frac {AE}{AD}=\frac {1}{2}=\frac {AD}{AB}$，又$\because ∠A=∠A$，$\therefore △AED\backsim △ADB,\therefore ∠AED=∠ADB=90^{\circ }$。$\because ∠A=∠C=60^{\circ },\frac {AD}{BC}=\frac {AE}{CD}=\frac {1}{2},\therefore △AED\backsim △CDB$。$\because ∠AED=∠DEB=90^{\circ },∠ADE=∠DBE=30^{\circ },\therefore △AED\backsim △DEB$。

10 易错题在平面直角坐标系中,O为坐标原点,已知点$A(-2,0),B(0,4),C(0,3)$,过点C作直线交x轴于点D,使得以D,O,C为顶点的三角形与$\triangle AOB$相似,这样的直线最多可以作 (4)
A. 2条
B. 3条
C. 4条
D. 6条

答案： C 若$△AOB\backsim △COD$，则$\frac {OA}{OC}=\frac {OB}{OD}$，即$\frac {2}{3}=\frac {4}{OD},\therefore OD=6$，则点$D$的坐标为$(6,0)$或$(-6,0)$。若$△AOB\backsim △DOC$，则$\frac {OA}{OD}=\frac {OB}{OC}$，即$\frac {2}{OD}=\frac {4}{3},\therefore OD=\frac {3}{2}$，则点$D$的坐标为$(\frac {3}{2},0)$或$(-\frac {3}{2},0)$。$\therefore$ 这样的直线最多可以作 4 条。

11 如图,在$\triangle ABC$中,BD,CE分别是AC,AB边上的高,连接ED.求证:$\triangle ABC\backsim \triangle ADE$.

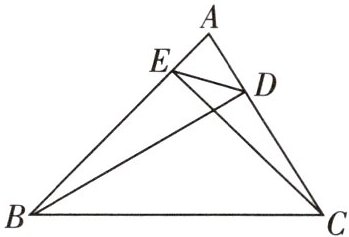
答案：
证明：如图，设$BD$与$CE$交于点$O$，
$\because BD,CE$分别是$AC,AB$边上的高，
$\therefore ∠ADB=∠AEC=90^{\circ }$，
又$\because ∠A=∠A,\therefore △ABD\backsim △ACE$，
$\therefore \frac {AB}{AC}=\frac {AD}{AE},\therefore \frac {AB}{AD}=\frac {AC}{AE}$，
又$\because ∠A=∠A,\therefore △ABC\backsim △ADE$。

12 如图,$\triangle ABC$是等边三角形,D为CB延长线上一点,E为BC延长线上一点.
(1)当BD,BC和CE满足什么条件时,$\triangle ADB\backsim \triangle EAC$?
答：当$BC^{2}=BD\cdot CE$时，$\triangle ADB\backsim \triangle EAC$。
(2)当$\triangle ADB\backsim \triangle EAC$时,求$∠DAE$的度数.
答：$∠DAE$的度数为$120^{\circ }$。

答案： 解题思路：（1）由等边三角形可得$AB=BC=CA,∠ABC=∠ACB=60^{\circ }$，则$∠ABD=∠ECA=120^{\circ }$，结合$BC^{2}=BD\cdot CE$可得$AB\cdot CA=BD\cdot CE$，即可得出答案；（2）由$△ADB\backsim △EAC$可得$∠D=∠CAE$，由$∠ABC=∠D+∠DAB=60^{\circ }$可得$∠CAE+∠DAB=60^{\circ }$，再结合$∠DAE=∠CAE+∠DAB+∠BAC$即可得出答案。
解：（1）当$BC^{2}=BD\cdot CE$时，$△ADB\backsim △EAC$。
$\because △ABC$是等边三角形，
$\therefore AB=BC=CA,∠ABC=∠ACB=60^{\circ }$，
$\therefore ∠ABD=∠ECA=120^{\circ }$，
$\because BC^{2}=BD\cdot CE,\therefore AB\cdot CA=BD\cdot CE$，
$\therefore \frac {AB}{EC}=\frac {BD}{CA},\therefore △ADB\backsim △EAC$。
（2）$\because △ADB\backsim △EAC,\therefore ∠D=∠CAE$，
$\because ∠ABC=∠D+∠DAB=60^{\circ },\therefore ∠CAE+∠DAB=60^{\circ }$，
$\therefore ∠DAE=∠CAE+∠DAB+∠BAC=60^{\circ }+60^{\circ }=120^{\circ }$。

13 几何直观[2024南阳期中]如图1,在矩形ABCD中,$AB= 2,BC= 5,BP= 1$,点M在CB的延长线上,$∠MPN= 90^{\circ }$.将$∠MPN$绕点P按顺时针方向旋转,PM交边AB(或边AD)于点E,PN交边AD(或边CD)于点F,当PN旋转至PC处时,$∠MPN$的旋转随即停止.
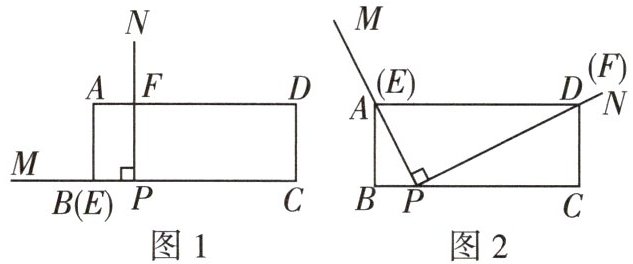
(1)特殊情形:如图2,发现当PM过点A时,PN也恰好过点D.此时,$\triangle ABP$____$\triangle PCD$(填“≌”或“∽”),并说明理由.
(2)类比探究:如图3,在旋转的过程中,$\frac {PE}{PF}$的值是否为定值? 若是,请求出该定值;若不是,请说明理由.

答案：
解：（1）$\backsim$
理由：$\because AB=2,PC=5-1=4,\therefore \frac {AB}{PC}=\frac {1}{2}$。
$\because BP=1,CD=2,\therefore \frac {BP}{CD}=\frac {1}{2},\therefore \frac {AB}{PC}=\frac {BP}{CD}$，
又$\because ∠B=∠C=90^{\circ },\therefore △ABP\backsim △PCD$。
（2）$\frac {PE}{PF}$的值为定值。理由如下：
如图，过点$F$作$FG⊥BC$于点$G$，则$FG=2$。
$\because ∠MPN=90^{\circ },\therefore ∠EPB+∠FPG=90^{\circ }$。
$\because ∠B=90^{\circ },\therefore ∠EPB+∠BEP=90^{\circ }$，
$\therefore ∠BEP=∠FPG$，
又$\because ∠B=∠PCG=90^{\circ },\therefore △EBP\backsim △PGF$，
$\therefore \frac {PE}{PF}=\frac {BP}{FG}=\frac {1}{2}$。