《2025年一遍过九年级初中数学上册北师大版》

1 [2024沧州期末]如图,网格中每个小正方形的边长均为1,$△OA_{1}B_{1}与△OAB$的形状相同,大小不同,$△OA_{1}B_{1}是由△OAB$的各顶点变化得到的,则各顶点变化情况为 (C)

A. 横坐标和纵坐标都加2
B. 横坐标和纵坐标都乘以2
C. 横坐标和纵坐标都除以2
D. 横坐标和纵坐标都减2

答案： C
∵$A_{1}(2,1),A(4,2),B_{1}(1,3),B(2,6)$，
∴各顶点变化情况为横坐标和纵坐标都除以 2.

2 [2024浙江中考]如图,在平面直角坐标系中,$△ABC与△A'B'C'$是位似图形,位似中心为点O.若点$A(-3,1)的对应点为A'(-6,2)$,则点$B(-2,4)的对应点B'$的坐标为 ((-4,8))
A.$(-4,8)$
B.$(8,-4)$
C.$(-8,4)$
D.$(4,-8)$

答案： A
∵△ABC 与△A'B'C'是位似图形，位似中心为点 O，点 A(−3,1)的对应点为 A'(−6,2)，
∴△ABC 与△A'B'C'的相似比为 1:2，
∵点 B 的坐标为(−2,4)，点 B 的对应点 B'的坐标为(−2×2,4×2)，即(−4,8).

3 [2025深圳南山区期末]如图,在平面直角坐标系中,$△ABC与△ADE$位似,相似比为$1:2$.已知位似中心点A的坐标为$(0,2)$,点B的坐标为$(1,4)$,则点D的坐标为 ( )


A.$(-2,-4)$
B.$(-2,-2)$
C.$(-4,-4)$
D.$(-4,-2)$

答案：
B 如图，过 B 作 BH⊥y 轴于点 H，过 D 作 DG⊥y 轴于点 G，
∴BH//DG，易得△ABH∽△ADG，
∴$\frac{AH}{AG}$=$\frac{BH}{DG}$=$\frac{AB}{AD}$，
∵△ABC 与△ADE 位似，相似比为 1:2，
∴$\frac{AB}{AD}$=$\frac{1}{2}$，
∴$\frac{AH}{AG}$=$\frac{BH}{DG}$=$\frac{1}{2}$，
∵点 A 的坐标为(0,2)，点 B 的坐标为(1,4)，
∴BH=1，OH=4，OA=2，
∴AH=2，AG=4，DG=2，
∴OG=2，
∴D(−2,−2).

4 [2023盘锦中考]如图,$△ABO的顶点分别是A(2,6)$,$B(3,1)$,$O(0,0)$,以点O为位似中心,将$△ABO缩小为原来的\frac {1}{3}$,得到$△A'B'O$,则点$A'$的坐标为($\frac{2}{3}$,2)或(−$\frac{2}{3}$，−2).

答案： ($\frac{2}{3}$,2)或(−$\frac{2}{3}$，−2) 分两种情况：当缩小后的三角形和△ABO 在原点 O 的同侧时，将点 A 的横、纵坐标分别乘$\frac{1}{3}$，得点 A'的坐标为($\frac{2}{3}$,2)；当缩小后的三角形和△ABO 在原点 O 的异侧时，将点 A 的横、纵坐标分别乘−$\frac{1}{3}$，得点 A'的坐标为(−$\frac{2}{3}$,−2).
名师点睛
当以原点为位似中心时，变换前后两个图形对应点坐标之比的绝对值等于相似比.

5 一题多解[2024漳州三中月考]如图,正方形OEFG和正方形ABCD是位似图形,且点F与点C是对应点,点F的坐标是$(1,1)$,点C的坐标是$(4,2)$,则它们的位似中心的坐标是____.

答案：
(−2,0) 解法一 如图，连接 CF 并延长，交 EB 所在的直线于点 P.
∵正方形 OEFG 和正方形 ABCD 是位似图形，点 F 与点 C 是对应点，
∴点 E 与点 B 是对应点，
∴点 P 为位似中心. 易知$\frac{EF}{BC}$=$\frac{1}{2}$，
∴正方形 OEFG 和正方形 ABCD 的相似比为 1:2，
∴$\frac{PE}{PB}$=$\frac{1}{2}$，即$\frac{PO+1}{PO+4}$=$\frac{1}{2}$，
∴PO=2. 故点 P 的坐标为(−2,0).

解法二
∵正方形 OEFG 和正方形 ABCD 是位似图形，点 F 与点 C 是对应点，
∴点 B 与点 E 是对应点，
∴它们的位似中心在 x 轴上，且在直线 CF 上. 设直线 CF 的函数表达式为 y=kx+b，则$\begin{cases}k + b = 1\\4k + b = 2\end{cases}$，解得$k=\frac{1}{3}$，$b=\frac{2}{3}$，
∴直线 CF 的函数表达式为$y=\frac{1}{3}x+\frac{2}{3}$，当 y = 0 时，x = −2，
∴它们的位似中心的坐标是(−2,0).

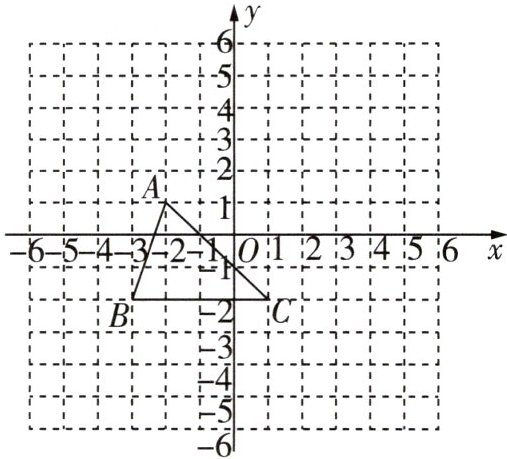
6 如图,方格纸中每个小方格都是边长为1的正方形,$△ABC$的顶点都在格点上,建立平面直角坐标系.
(1)点A的坐标为____,点B的坐标为____,点C的坐标为____;
(2)以原点O为位似中心,将$△ABC$放大,使变换后的三角形与$△ABC的相似比为2:1$,请在网格内画出它的位似图形;
(3)求出变换后的三角形的面积.

答案：
解：
(1) (−2,1) (−3,−2) (1,−2)
(2) 分两种情况，△$A_{1}B_{1}C_{1}$ 和△$A_{2}B_{2}C_{2}$ 即所求，如图所示.

(3) 变换后的三角形的面积为$\frac{1}{2}×8×6 = 24$.

【回顾与思考】
如何将一个图形放大或缩小?

答案： 【解析】：将一个图形放大或缩小可以通过以下方法：
1. 确定比例：明确放大或缩小的比例，例如放大为原来的2倍，缩小为原来的1/2等。
2. 选取关键点：在原图形上选取一些关键的点，如多边形的顶点等。
3. 计算新位置：根据确定的比例，计算这些关键点放大或缩小后的新位置。如果是在平面直角坐标系中，对于点(x,y)，若放大或缩小比例为k，则新的坐标为(kx,ky)。
4. 连接新点：按照原图形中关键点的连接顺序，连接放大或缩小后关键点的新位置，从而得到放大或缩小后的新图形。
【答案】：先确定放大或缩小的比例，选取原图形的关键点，根据比例计算关键点放大或缩小后的新位置，最后连接新点得到新图形。