《2025年一遍过九年级初中数学上册北师大版》

1 [2025 秦皇岛月考]在△ABC 中,已知 AB = 5,BC = 4,AC = 8,若$△ABC ∽ △A_1B_1C_1,△A_1B_1C_1$的最长边的长为 16,则其他两边的长分别为 (B)
A. $A_1B_1 = 8,B_1C_1 = 10$
B. $A_1B_1 = 10,B_1C_1 = 8$
C. $A_1B_1 = 5,B_1C_1 = 8$
D. $A_1B_1 = 10,B_1C_1 = 4$

答案： B
∵ 两个三角形中最长边和最长边是对应边，$\triangle ABC \sim \triangle A_1B_1C_1$，$\therefore \frac{AB}{A_1B_1} = \frac{BC}{B_1C_1} = \frac{AC}{A_1C_1}$，$\therefore \frac{5}{A_1B_1} = \frac{4}{B_1C_1} = \frac{8}{16}$，$\therefore A_1B_1 = 10$，$B_1C_1 = 8$。

2 教材 P90 习题 T1 变式 如图,△ABC ∽ △ACP,若∠A = 75°,∠APC = 65°,则∠B 的度数为 (40°)

A. 40°
B. 50°
C. 65°
D. 75°

答案： A
∵ $\angle A = 75^\circ$，$\angle APC = 65^\circ$，$\therefore \angle ACP = 40^\circ$。
∵ $\triangle ABC \sim \triangle ACP$，$\therefore \angle B = \angle ACP = 40^\circ$。
归纳总结
相似三角形的对应角、对应边的找法与全等三角形的对应角、对应边的找法一样，一般地，公共角、对顶角等是对应角，最大（小）的角对应最大（小）的角，最长（短）的边对应最长（短）的边。

3 教材 P90 随堂练习 T1 变式 [2025 驻马店期中]如果两个三角形满足下列条件,那么它们一定相似的是 (C)
A. 有一个角相等的两个等腰三角形
B. 有一个角相等的两个直角三角形
C. 有一个角是 100°的两个等腰三角形
D. 有一组角是对顶角的两个三角形

答案： C 有一个角是 $100^\circ$ 的等腰三角形，$100^\circ$ 的角一定是其顶角，这样的两个等腰三角形一定相似。

4 教材 P90 习题 T2 变式 如图,在平行四边形 ABCD 中,E 为 CD 延长线上一点,连接 BE 交 AD 于点 F,连接 AE,则图中与△DEF 相似的三角形共有 (B)

A. 1 个
B. 2 个
C. 3 个
D. 4 个

答案： B 因为四边形 $ABCD$ 是平行四边形，所以 $AD // BC$，$AB // DC$，所以 $\angle EFD = \angle EBC$，$\angle EDF = \angle C$，$\angle ABF = \angle DEF$，$\angle BAF = \angle EDF$，所以 $\triangle DEF \sim \triangle CEB$，$\triangle ABF \sim \triangle DEF$。

5 [2024 杭州星澜中学月考]如图,在△ABC 中,AD 是中线,BC = 8,∠B = ∠DAC,则线段 AC 的长为 (4√2)
A. 4
B. 4√2
C. 6
D. 4√3

答案： B
∵ $\angle B = \angle DAC$，$\angle C = \angle C$，$\therefore \triangle CAD \sim \triangle CBA$，$\therefore \frac{AC}{BC} = \frac{DC}{AC}$。
∵ $AD$ 是中线，$BC = 8$，$\therefore BD = DC = 4$，$\therefore \frac{AC}{8} = \frac{4}{AC}$，$\therefore AC = 4\sqrt{2}$（$-4\sqrt{2}$ 舍去）。

6 [2025 菏泽月考]如图,在△ABC 中,AB = AC,点 P 为 BC 边上一动点(不与点 B,C 重合),连接 AP,过点 P 作射线 PM 交 AC 于点 M,使∠APM = ∠B. △ABP 与△PCM 相似吗? 为什么?

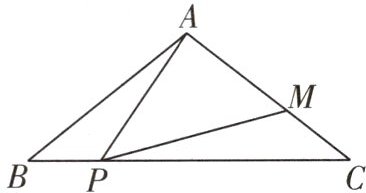
解：△ABP∽△PCM。理由如下：
∵ AB = AC，∴ ∠B = ∠C。
∵ ∠APC = ∠B + ∠BAP，∠APM = ∠B，∠APC = ∠APM + ∠CPM，∴ ∠BAP = ∠CPM，
∴ △ABP∽△PCM。

答案： 解：$\triangle ABP \sim \triangle PCM$。理由如下：
∵ $AB = AC$，$\therefore \angle B = \angle C$。
∵ $\angle APC = \angle B + \angle BAP$，$\angle APM = \angle B$，$\angle APC = \angle APM + \angle CPM$，$\therefore \angle BAP = \angle CPM$，
$\therefore \triangle ABP \sim \triangle PCM$。

7 教材 P91T5 变式 [2025 榆林期中]西安地处陕西肥沃的关中平原中部,古称长安,是十三朝古都,中华文明的重要发祥地之一,北濒渭河,南依秦岭,山水相连,素有“八水绕长安”的美称. 如图,为了测量渭河支流上某段的宽度,在河的对岸选定一个目标点 P,在近岸取点 Q 和 S,使点 P,Q,S 在一条直线上,且直线 PS 与河垂直,在过点 S 且与直线 PS 垂直的直线 a 上选择适当的点 T,PT 与过点 Q 且与 PS 垂直的直线 b 交于点 R. 如果 QS = 60 m,ST = 120 m,QR = 80 m,试求该段河的大致宽度 PQ.

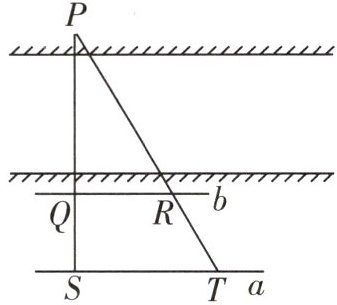
解：根据题意，得 $QR \perp PS$，$ST \perp PS$，
$\therefore \angle PQR = \angle PST = 90^\circ$，
∵ $\angle QPR = \angle SPT$，$\therefore \triangle PQR \sim \triangle PST$，$\therefore \frac{PQ}{PS} = \frac{QR}{ST}$。
∵ $QS = 60\ \text{m}$，$ST = 120\ \text{m}$，$QR = 80\ \text{m}$，
$\therefore \frac{PQ}{60 + PQ} = \frac{80}{120}$，$\therefore PQ = $120$\ \text{m}$，
$\therefore$ 该段河的大致宽度 $PQ$ 为 120$\ \text{m}$。

答案： 解：根据题意，得 $QR \perp PS$，$ST \perp PS$，
$\therefore \angle PQR = \angle PST = 90^\circ$，
∵ $\angle QPR = \angle SPT$，$\therefore \triangle PQR \sim \triangle PST$，$\therefore \frac{PQ}{PS} = \frac{QR}{ST}$。
∵ $QS = 60\ \text{m}$，$ST = 120\ \text{m}$，$QR = 80\ \text{m}$，
$\therefore \frac{PQ}{60 + PQ} = \frac{80}{120}$，$\therefore PQ = 120\ \text{m}$，
$\therefore$ 该段河的大致宽度 $PQ$ 为 $120\ \text{m}$。