《2025年一遍过九年级初中数学上册北师大版》

10 [2023 兰州中考]如图,在矩形 ABCD 中,点 E 为 BA 延长线上一点,F 为 CE 的中点,以 B 为圆心,BF 长为半径的圆弧过 AD 与 CE 的交点 G,连接 BG。若 $ AB = 4 $,$ CE = 10 $,则 $ AG = $(3)

A. 2
B. 2.5
C. 3
D. 3.5

答案： C
∵四边形ABCD为矩形，
∴∠ABC = ∠BAD = 90°。在Rt△BCE中，点F为斜边CE的中点，
∴BF = $\frac{1}{2}$CE = 5，
∴BG = BF = 5。在Rt△ABG中，AB = 4，BG = 5，由勾股定理得，AG = $\sqrt{BG^{2}-AB^{2}}$ = 3。

11 新考法 [2024 郑州十九中期中]如图,在 $ △ABC $中,$ AB = 10 $,$ AC = 8 $,$ BC = 6 $,线段 DE 的两个端点 D,E 分别在边 AC,BC 上滑动,且 $ DE = 4 $,若点 M,N 分别是 DE,AB 的中点,则 MN 的最小值为( )
A. 2
B. 3
C. 3.5
D. 4

答案：
B 如图，连接CM，CN，在△ABC中，AB = 10，AC = 8，BC = 6，
∴AB² = AC² + BC²，
∴△ABC是直角三角形，且∠ACB = 90°。
∵DE = 4，点M，N分别是DE，AB的中点，
∴CN = $\frac{1}{2}$AB = 5，CM = $\frac{1}{2}$DE = 2，当C，M，N在同一直线上时，MN取得最小值，（在△CMN中，MN ＞ CN - CM，当C，M，N在同一直线上时，MN = CN - CM）MN的最小值为5 - 2 = 3。

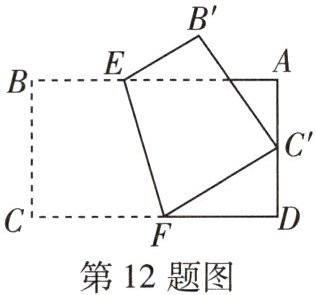
12 [2024 山西省实验中学月考]如图,将矩形纸片 ABCD 沿直线 EF 折叠,使点 C 落在 AD 边的中点 $ C' $处,点 B 落在点 $ B' $处,若 $ AB = 9 $,$ BC = 6 $,则 $ FC' $的长为______5。

答案： 5 由题意可知，C'D = $\frac{1}{2}$AD = $\frac{1}{2}$BC = 3。设CF = x，则FC' = x，DF = 9 - x。在Rt△C'DF中，DF² + C'D² = FC'²，即(9 - x)² + 3² = x²，解得x = 5，所以FC' = 5。
解题通法
利用矩形的性质求线段长的常用方法
(1) 把所要求的线段放在直角三角形中，使其成为某条边，利用勾股定理或借助特殊角(30°，45°)求解；
(2) 利用矩形的性质构造全等三角形，将未知线段转化为已知线段。

13 [2025 西安曲江一中月考]如图,矩形 ABCD 的对角线相交于点 O,过点 O 作 $ OG ⊥ AC $,交 AB 于点 G,连接 CG,若 $ ∠BOG = 16^\circ $,则 $ ∠BCG $的度数是16°。

答案： 16°
∵四边形ABCD是矩形，
∴AC = BD，AB//DC，DO = OA = OB = OC，
∴∠OCB = ∠OBC。
∵OG⊥AC，
∴OG是AC的垂直平分线，
∴AG = CG，
∴∠OAG = ∠OCG。
∵AB//DC，
∴∠OAG = ∠OCD，
∵∠BOG = 16°，∠COG = 90°，
∴∠COB = 74°。
∵∠OCB = ∠OBC，
∴∠OCB = ∠OBC = $\frac{180° - 74°}{2}$ = 53°，
∵∠BCD = 90°，
∴∠OCD = ∠BCD - ∠OCB = 90° - 53° = 37°，
∴∠OCG = ∠OAG = ∠OCD = 37°，
∴∠BCG = ∠OCB - ∠OCG = 53° - 37° = 16°。

14 [2025 榆林六中月考]如图,在矩形 ABCD 中,O 为对角线 AC,BD 的交点,过点 O 的直线分别与边 DA,BC 延长线交于点 E,F。
(1)求证：$ AE = CF $。
证明：∵四边形ABCD是矩形，∴OA = OC，AD//BC，∴∠OAE = ∠OCF。在△OAE和△OCF中，$\begin{cases}\angle OAE = \angle OCF\\OA = OC\\\angle AOE = \angle COF\end{cases}$，∴△OAE≌△OCF(ASA)，∴AE = CF。
(2)若 $ ∠ADB = 2∠E $,求证：$ AE = \frac{1}{2}BD $。
证明：∵四边形ABCD是矩形，∴AC = BD，OA = $\frac{1}{2}$AC，OD = $\frac{1}{2}$BD，∴OA = OD，∴∠OAD = ∠ADB，设∠E = x，则∠ADB = 2x，∴∠OAD = 2x，∵∠OAD = ∠E + ∠AOE，∴∠E = ∠AOE，∴AE = AO，∴AE = $\frac{1}{2}$AC = $\frac{1}{2}$BD。

答案： 证明：
(1)
∵四边形ABCD是矩形，
∴OA = OC，AD//BC，
∴∠OAE = ∠OCF。在△OAE和△OCF中，$\begin{cases}\angle OAE = \angle OCF\\OA = OC\\\angle AOE = \angle COF\end{cases}$，
∴△OAE≌△OCF(ASA)，
∴AE = CF。
(2)
∵四边形ABCD是矩形，
∴AC = BD，OA = $\frac{1}{2}$AC，OD = $\frac{1}{2}$BD，
∴OA = OD，
∴∠OAD = ∠ADB，设∠E = x，则∠ADB = 2x，
∴∠OAD = 2x，
∵∠OAD = ∠E + ∠AOE，
∴∠E = ∠AOE，
∴AE = AO，
∴AE = $\frac{1}{2}$AC = $\frac{1}{2}$BD。

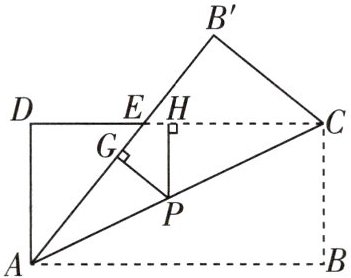
15 一题多解 [2025 吉安月考]如图,将矩形纸片 ABCD 沿对角线 AC 折叠,使点 B 落到点 $ B' $的位置,$ AB' $与 CD 交于点 E。
(1)试找出一个与 $ △AED $全等的三角形,并加以证明；
(2)若 $ AB = 8 $,$ DE = 3 $,P 为线段 AC 上的任意一点,$ PG ⊥ AB' $于点 G,$ PH ⊥ DC $于点 H,试求 $ PG + PH $的值。

(1) △AED≌△CEB'。证明如下：∵四边形ABCD为矩形，∴AD = BC，∠D = ∠B = 90°，由折叠，得BC = B'C，∠B = ∠B' = 90°，∴AD = CB'，∠D = ∠B'，又∵∠DEA = ∠B'EC，∴△AED≌△CEB'。
(2) 4

答案： 解：
(1) △AED≌△CEB'。证明如下：
∵四边形ABCD为矩形，
∴AD = BC，∠D = ∠B = 90°，由折叠，得BC = B'C，∠B = ∠B' = 90°，
∴AD = CB'，∠D = ∠B'，又
∵∠DEA = ∠B'EC，
∴△AED≌△CEB'。
(2) 解法一 由已知得∠EAC = ∠CAB，且∠CAB = ∠ECA，
∴∠EAC = ∠ECA，
∴AE = EC = 8 - 3 = 5。在Rt△ADE中，AD = $\sqrt{AE^{2}-DE^{2}}$ = 4。延长HP交AB于点M，则PM⊥AB，
∵∠CAB' = ∠CAB，PG⊥AB'，PM⊥AB，
∴PG = PM，
∴PG + PH = PM + PH = HM = AD = 4。
解法二 连接PE。
∵S△EAC = S△EAP + S△EPC，
∴$\frac{1}{2}$EC·AD = $\frac{1}{2}$AE·PG + $\frac{1}{2}$CE·PH。由
(1)得AE = CE，
∴PG + PH = AD。同解法一可得AD = 4，
∴PG + PH = 4。

16 几何直观 [2024 牡丹江中考]矩形 ABCD 的面积是 90,对角线 AC,BD 交于点 O,点 E 是 BC 边的三等分点,连接 DE,点 P 是 DE 的中点,$ OP = 3 $,连接 CP,则 $ PC + PE $的值为______。

答案：
13或$\sqrt{109}$ 当CE ＞ BE时，如图1，在矩形ABCD中，∠ECD = 90°，点O是BD的中点，点P是DE的中点，
∴BE = 2OP = 6，CP = PE = PD，
∵点E是BC边的三等分点，
∴CE = 2BE = 12，BC = 3BE = 18。
∵矩形ABCD的面积是90，
∴BC·CD = 90，
∴CD = 5，
∴DE = $\sqrt{5^{2}+12^{2}}$ = 13，
∴PC + PE = DE = 13。当CE ＜ BE时，如图2，在矩形ABCD中，点O是BD的中点，点P是DE的中点，
∴BE = 2OP = 6，CP = PE = PD。
∵点E是BC边的三等分点，
∴CE = $\frac{1}{2}$BE = 3，BC = 3 + 6 = 9。
∵矩形ABCD的面积是90，
∴BC·CD = 90，
∴CD = 10，
∴DE = $\sqrt{3^{2}+10^{2}}$ = $\sqrt{109}$，
∴PC + PE = DE = $\sqrt{109}$。