第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
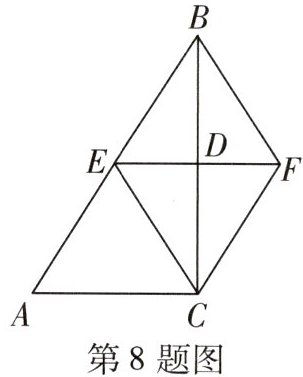
8 [2025佛山月考]如图,在$ △ABC $中,$ ∠ACB = 90° $,BC的垂直平分线EF交BC于点D,交AB于点E,且$ BE = BF $,为了使四边形BECF是正方形,可以添加一个条件 (
A. $ CE = CF $
B. $ DE = DF $
C. $ ∠A = 45° $
D. E为AB的中点
C
)
A. $ CE = CF $
B. $ DE = DF $
C. $ ∠A = 45° $
D. E为AB的中点
答案:
C $\because BC$的垂直平分线$EF$交$BC$于点$D$,交$AB$于点$E$,$\therefore BD = DC$,$EF\perp BC$,$EB = EC$,$FB = FC$.$\because BE = BF$,$\therefore BE = BF = EC = FC$,$\therefore$四边形$BECF$是菱形.当添加$CE = CF$时,则$BE = BF = EC = CF$,$\therefore$四边形$BECF$是菱形.当添加$DE = DF$时,则四边形$BECF$是平行四边形.$\because BE = BF$,$\therefore$四边形$BECF$是菱形.当添加$\angle A = 45^{\circ}$时,$\because\angle ACB = 90^{\circ}$,$\therefore\angle ABC = \angle ECB = 45^{\circ}$,$\therefore\angle BEC = 90^{\circ}$,$\therefore$菱形$BECF$是正方形.当添加$E$为$AB$的中点时,得到$BE = CE$,无法判定菱形$BECF$是正方形.
9 [2024福州十九中期中]如图,在$ △ABC $中,$ AB = AC = 13 $,$ BC = 10 $,D在$ △ABC $内,且$ BD = CD $,$ ∠BDC = 90° $,E,F,G,H分别是AB,AC,BD,CD的中点,则四边形EFHG的面积为____.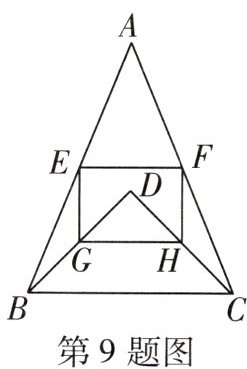

答案:
$\frac{35}{2}$ 如图,连接$AD$并延长交$BC$于点$P$,$\because AB = AC$,$BD = CD$,$\therefore AP$是线段$BC$的垂直平分线,$\therefore BP = CP = 5$,$AP\perp BC$.在$\text{Rt}\triangle BDC$中,$\angle BDC = 90^{\circ}$,$BP = CP$,$\therefore DP = \frac{1}{2}BC = 5$.在$\text{Rt}\triangle APB$中,$AP=\sqrt{AB^{2}-BP^{2}} = 12$,$\therefore AD = 12 - 5 = 7$.
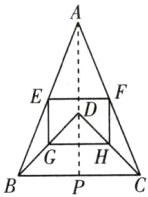
$\because E$,$F$分别是$AB$,$AC$的中点,$\therefore EF$是$\triangle ABC$的中位线,$\therefore EF=\frac{1}{2}BC = 5$,$EF// BC$,同理,$GH = \frac{1}{2}BC$,$GH// BC$,$EG=\frac{1}{2}AD=\frac{7}{2}$,$EG// AD$,$\therefore GH = EF$,$GH// EF$,$\therefore$四边形$EFHG$为平行四边形.$\because EF// BC$,$EG// AD$,$AP\perp BC$,$\therefore EF\perp EG$,$\therefore$四边形$EFHG$为矩形,$\therefore$四边形$EFHG$的面积为$5×\frac{7}{2}=\frac{35}{2}$.
$\frac{35}{2}$ 如图,连接$AD$并延长交$BC$于点$P$,$\because AB = AC$,$BD = CD$,$\therefore AP$是线段$BC$的垂直平分线,$\therefore BP = CP = 5$,$AP\perp BC$.在$\text{Rt}\triangle BDC$中,$\angle BDC = 90^{\circ}$,$BP = CP$,$\therefore DP = \frac{1}{2}BC = 5$.在$\text{Rt}\triangle APB$中,$AP=\sqrt{AB^{2}-BP^{2}} = 12$,$\therefore AD = 12 - 5 = 7$.

$\because E$,$F$分别是$AB$,$AC$的中点,$\therefore EF$是$\triangle ABC$的中位线,$\therefore EF=\frac{1}{2}BC = 5$,$EF// BC$,同理,$GH = \frac{1}{2}BC$,$GH// BC$,$EG=\frac{1}{2}AD=\frac{7}{2}$,$EG// AD$,$\therefore GH = EF$,$GH// EF$,$\therefore$四边形$EFHG$为平行四边形.$\because EF// BC$,$EG// AD$,$AP\perp BC$,$\therefore EF\perp EG$,$\therefore$四边形$EFHG$为矩形,$\therefore$四边形$EFHG$的面积为$5×\frac{7}{2}=\frac{35}{2}$.
10 [2024九江柴桑区期中]如图,在矩形ABCD中,M,N分别是AD,BC的中点,P,Q分别是BM,DN的中点.
(1)求证:$ BM // DN $.
(2)求证:四边形MPNQ是菱形.
(3)矩形ABCD的边AB与AD满足什么数量关系时,四边形MPNQ为正方形?请说明理由.
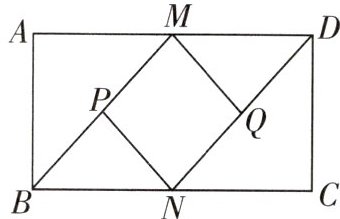
(1)证明:$\because$四边形$ABCD$是矩形,
$\therefore AD// BC$,$AD = BC$,
又$\because M$,$N$分别是$AD$,$BC$的中点,
$\therefore DM = BN$,$\therefore$四边形$DMBN$是平行四边形,
$\therefore BM// DN$.
(2)证明:由(1)知$BM = DN$,$BM// DN$,$\therefore MP// NQ$,
$\because P$,$Q$分别是$BM$,$DN$的中点,$\therefore MP = NQ$,
$\therefore$四边形$MPNQ$是平行四边形.
连接$MN$,
$\because$四边形$ABCD$是矩形,$\therefore AD// BC$,$AD = BC$,$\angle C = 90^{\circ}$.
又$\because M$,$N$分别是$AD$,$BC$的中点,$\therefore DM = CN$,
$\therefore$四边形$DMNC$是矩形.
$\because DN$是矩形$DMNC$的对角线,且$Q$是$DN$的中点,
$\therefore MQ = NQ$,
$\therefore$平行四边形$MPNQ$是菱形.
(3)解:当$AB=$
$\because AB=\frac{1}{2}AD$,$DM=\frac{1}{2}AD$,$AB = CD$,
$\therefore CD = DM$,$\therefore$矩形$DMNC$是正方形.
$\because Q$为正方形$DMNC$对角线$DN$的中点,$\therefore\angle NQM = 90^{\circ}$.
又$\because$四边形$MPNQ$是菱形,$\therefore$四边形$MPNQ$是正方形.
解题通法
探究性试题的求解思路
求解探究题时往往把结论反过来当条件用,需要执果索因,逆向推理,逐步探求使结论成立的条件;也可假设结论的某一方面存在,然后在这个假设下进行合情推理,若推出矛盾即可否定假设,若推出合理的结论,则可肯定假设.
(1)求证:$ BM // DN $.
(2)求证:四边形MPNQ是菱形.
(3)矩形ABCD的边AB与AD满足什么数量关系时,四边形MPNQ为正方形?请说明理由.

(1)证明:$\because$四边形$ABCD$是矩形,
$\therefore AD// BC$,$AD = BC$,
又$\because M$,$N$分别是$AD$,$BC$的中点,
$\therefore DM = BN$,$\therefore$四边形$DMBN$是平行四边形,
$\therefore BM// DN$.
(2)证明:由(1)知$BM = DN$,$BM// DN$,$\therefore MP// NQ$,
$\because P$,$Q$分别是$BM$,$DN$的中点,$\therefore MP = NQ$,
$\therefore$四边形$MPNQ$是平行四边形.
连接$MN$,
$\because$四边形$ABCD$是矩形,$\therefore AD// BC$,$AD = BC$,$\angle C = 90^{\circ}$.
又$\because M$,$N$分别是$AD$,$BC$的中点,$\therefore DM = CN$,
$\therefore$四边形$DMNC$是矩形.
$\because DN$是矩形$DMNC$的对角线,且$Q$是$DN$的中点,
$\therefore MQ = NQ$,
$\therefore$平行四边形$MPNQ$是菱形.
(3)解:当$AB=$
$\frac{1}{2}AD$
时,四边形$MPNQ$为正方形.理由如下:$\because AB=\frac{1}{2}AD$,$DM=\frac{1}{2}AD$,$AB = CD$,
$\therefore CD = DM$,$\therefore$矩形$DMNC$是正方形.
$\because Q$为正方形$DMNC$对角线$DN$的中点,$\therefore\angle NQM = 90^{\circ}$.
又$\because$四边形$MPNQ$是菱形,$\therefore$四边形$MPNQ$是正方形.
解题通法
探究性试题的求解思路
求解探究题时往往把结论反过来当条件用,需要执果索因,逆向推理,逐步探求使结论成立的条件;也可假设结论的某一方面存在,然后在这个假设下进行合情推理,若推出矛盾即可否定假设,若推出合理的结论,则可肯定假设.
答案:
(1)证明:$\because$四边形$ABCD$是矩形,
$\therefore AD// BC$,$AD = BC$,
又$\because M$,$N$分别是$AD$,$BC$的中点,
$\therefore DM = BN$,$\therefore$四边形$DMBN$是平行四边形,
$\therefore BM// DN$.
(2)证明:由
(1)知$BM = DN$,$BM// DN$,$\therefore MP// NQ$,
$\because P$,$Q$分别是$BM$,$DN$的中点,$\therefore MP = NQ$,
$\therefore$四边形$MPNQ$是平行四边形.
连接$MN$,
$\because$四边形$ABCD$是矩形,$\therefore AD// BC$,$AD = BC$,$\angle C = 90^{\circ}$.
又$\because M$,$N$分别是$AD$,$BC$的中点,$\therefore DM = CN$,
$\therefore$四边形$DMNC$是矩形.
$\because DN$是矩形$DMNC$的对角线,且$Q$是$DN$的中点,
$\therefore MQ = NQ$,
$\therefore$平行四边形$MPNQ$是菱形.
(3)解:当$AB=\frac{1}{2}AD$时,四边形$MPNQ$为正方形.理由如下:
$\because AB=\frac{1}{2}AD$,$DM=\frac{1}{2}AD$,$AB = CD$,
$\therefore CD = DM$,$\therefore$矩形$DMNC$是正方形.
$\because Q$为正方形$DMNC$对角线$DN$的中点,$\therefore\angle NQM = 90^{\circ}$.
又$\because$四边形$MPNQ$是菱形,$\therefore$四边形$MPNQ$是正方形.
解题通法
探究性试题的求解思路
求解探究题时往往把结论反过来当条件用,需要执果索因,逆向推理,逐步探求使结论成立的条件;也可假设结论的某一方面存在,然后在这个假设下进行合情推理,若推出矛盾即可否定假设,若推出合理的结论,则可肯定假设.
(1)证明:$\because$四边形$ABCD$是矩形,
$\therefore AD// BC$,$AD = BC$,
又$\because M$,$N$分别是$AD$,$BC$的中点,
$\therefore DM = BN$,$\therefore$四边形$DMBN$是平行四边形,
$\therefore BM// DN$.
(2)证明:由
(1)知$BM = DN$,$BM// DN$,$\therefore MP// NQ$,
$\because P$,$Q$分别是$BM$,$DN$的中点,$\therefore MP = NQ$,
$\therefore$四边形$MPNQ$是平行四边形.
连接$MN$,
$\because$四边形$ABCD$是矩形,$\therefore AD// BC$,$AD = BC$,$\angle C = 90^{\circ}$.
又$\because M$,$N$分别是$AD$,$BC$的中点,$\therefore DM = CN$,
$\therefore$四边形$DMNC$是矩形.
$\because DN$是矩形$DMNC$的对角线,且$Q$是$DN$的中点,
$\therefore MQ = NQ$,
$\therefore$平行四边形$MPNQ$是菱形.
(3)解:当$AB=\frac{1}{2}AD$时,四边形$MPNQ$为正方形.理由如下:
$\because AB=\frac{1}{2}AD$,$DM=\frac{1}{2}AD$,$AB = CD$,
$\therefore CD = DM$,$\therefore$矩形$DMNC$是正方形.
$\because Q$为正方形$DMNC$对角线$DN$的中点,$\therefore\angle NQM = 90^{\circ}$.
又$\because$四边形$MPNQ$是菱形,$\therefore$四边形$MPNQ$是正方形.
解题通法
探究性试题的求解思路
求解探究题时往往把结论反过来当条件用,需要执果索因,逆向推理,逐步探求使结论成立的条件;也可假设结论的某一方面存在,然后在这个假设下进行合情推理,若推出矛盾即可否定假设,若推出合理的结论,则可肯定假设.
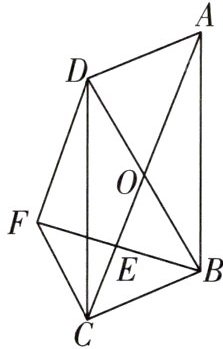
11 [2024青岛一模]如图,平行四边形ABCD的对角线AC,BD交于点O,E为OC的中点,过点C作$ CF // BD $交BE的延长线于F,连接DF.
(1)求证:$ △FCE ≌ △BOE $.
(2)若$ AD = CD $,当$ △ADC $满足什么条件时,四边形OCFD为正方形?请说明理由.
(1)证明:$\because CF// BD$,$\therefore\angle CFE = \angle OBE$,
$\because E$是$OC$的中点,$\therefore CE = OE$,
在$\triangle FCE$和$\triangle BOE$中,$\begin{cases}\angle CFE = \angle OBE,\\\angle CEF = \angle OEB,\\CE = OE,\end{cases}$
$\therefore\triangle FCE\cong\triangle BOE$(
(2)解:当$ △ADC $满足
$\because\triangle FCE\cong\triangle BOE$,$\therefore CF = OB$,
$\because$四边形$ABCD$是平行四边形,
$\therefore OA = OC$,$OB = OD$,$\therefore CF = OD$,
$\because CF// BD$,$\therefore$四边形$OCFD$为平行四边形,
$\because AD = CD$,$OA = OC$,
$\therefore OD\perp AC$,$\therefore\angle COD = 90^{\circ}$,
$\therefore$平行四边形$OCFD$为矩形.
$\because\angle ADC = 90^{\circ}$,$\therefore OC = OD$,
$\therefore$四边形$OCFD$为正方形.
(1)求证:$ △FCE ≌ △BOE $.
(2)若$ AD = CD $,当$ △ADC $满足什么条件时,四边形OCFD为正方形?请说明理由.

(1)证明:$\because CF// BD$,$\therefore\angle CFE = \angle OBE$,
$\because E$是$OC$的中点,$\therefore CE = OE$,
在$\triangle FCE$和$\triangle BOE$中,$\begin{cases}\angle CFE = \angle OBE,\\\angle CEF = \angle OEB,\\CE = OE,\end{cases}$
$\therefore\triangle FCE\cong\triangle BOE$(
AAS
).(2)解:当$ △ADC $满足
$\angle ADC = 90^{\circ}$
时,四边形OCFD为正方形.理由如下:$\because\triangle FCE\cong\triangle BOE$,$\therefore CF = OB$,
$\because$四边形$ABCD$是平行四边形,
$\therefore OA = OC$,$OB = OD$,$\therefore CF = OD$,
$\because CF// BD$,$\therefore$四边形$OCFD$为平行四边形,
$\because AD = CD$,$OA = OC$,
$\therefore OD\perp AC$,$\therefore\angle COD = 90^{\circ}$,
$\therefore$平行四边形$OCFD$为矩形.
$\because\angle ADC = 90^{\circ}$,$\therefore OC = OD$,
$\therefore$四边形$OCFD$为正方形.
答案:
(1)证明:$\because CF// BD$,$\therefore\angle CFE = \angle OBE$,
$\because E$是$OC$的中点,$\therefore CE = OE$,
在$\triangle FCE$和$\triangle BOE$中,$\begin{cases}\angle CFE = \angle OBE,\\\angle CEF = \angle OEB,\\CE = OE,\end{cases}$
$\therefore\triangle FCE\cong\triangle BOE(\text{AAS})$.
(2)解:当$\triangle ADC$满足$\angle ADC = 90^{\circ}$时,四边形$OCFD$为正方形.理由如下:
$\because\triangle FCE\cong\triangle BOE$,$\therefore CF = OB$,
$\because$四边形$ABCD$是平行四边形,
$\therefore OA = OC$,$OB = OD$,$\therefore CF = OD$,
$\because CF// BD$,$\therefore$四边形$OCFD$为平行四边形,
$\because AD = CD$,$OA = OC$,
$\therefore OD\perp AC$,$\therefore\angle COD = 90^{\circ}$,
$\therefore$平行四边形$OCFD$为矩形.
$\because\angle ADC = 90^{\circ}$,$\therefore OC = OD$,
$\therefore$四边形$OCFD$为正方形.
(1)证明:$\because CF// BD$,$\therefore\angle CFE = \angle OBE$,
$\because E$是$OC$的中点,$\therefore CE = OE$,
在$\triangle FCE$和$\triangle BOE$中,$\begin{cases}\angle CFE = \angle OBE,\\\angle CEF = \angle OEB,\\CE = OE,\end{cases}$
$\therefore\triangle FCE\cong\triangle BOE(\text{AAS})$.
(2)解:当$\triangle ADC$满足$\angle ADC = 90^{\circ}$时,四边形$OCFD$为正方形.理由如下:
$\because\triangle FCE\cong\triangle BOE$,$\therefore CF = OB$,
$\because$四边形$ABCD$是平行四边形,
$\therefore OA = OC$,$OB = OD$,$\therefore CF = OD$,
$\because CF// BD$,$\therefore$四边形$OCFD$为平行四边形,
$\because AD = CD$,$OA = OC$,
$\therefore OD\perp AC$,$\therefore\angle COD = 90^{\circ}$,
$\therefore$平行四边形$OCFD$为矩形.
$\because\angle ADC = 90^{\circ}$,$\therefore OC = OD$,
$\therefore$四边形$OCFD$为正方形.
【回顾与思考】
研究平行四边形的经验对于认识特殊平行四边形有怎样的帮助?
研究平行四边形的经验对于认识特殊平行四边形有怎样的帮助?
答案:
【解析】:研究平行四边形的经验为认识特殊平行四边形提供了基础和方法。在研究平行四边形时,我们学习了其定义、性质(如对边平行且相等、对角相等、对角线互相平分等)和判定方法。对于特殊平行四边形(如矩形、菱形、正方形),它们首先是平行四边形,具备平行四边形的一般性质。我们可以基于平行四边形的研究方法,从边、角、对角线等方面去进一步探究特殊平行四边形的特殊性质。例如,矩形是有一个角是直角的平行四边形,我们在平行四边形性质的基础上,重点研究直角这个特殊条件带来的新性质,如四个角都是直角、对角线相等。菱形是邻边相等的平行四边形,我们就着重研究邻边相等这个条件产生的特殊性质,如四条边都相等、对角线互相垂直且平分每一组对角。正方形既是矩形又是菱形,它综合了矩形和菱形的所有特殊性质。在判定方面,也是在平行四边形判定的基础上,增加特殊条件来判定特殊平行四边形。所以研究平行四边形的经验有助于我们更系统、更深入地认识特殊平行四边形。
【答案】:研究平行四边形的经验为认识特殊平行四边形提供了基础和方法,可基于平行四边形的研究方法从边、角、对角线等方面探究特殊平行四边形的特殊性质,在判定上也是在平行四边形判定基础上增加特殊条件来判定特殊平行四边形。
【答案】:研究平行四边形的经验为认识特殊平行四边形提供了基础和方法,可基于平行四边形的研究方法从边、角、对角线等方面探究特殊平行四边形的特殊性质,在判定上也是在平行四边形判定基础上增加特殊条件来判定特殊平行四边形。
查看更多完整答案,请扫码查看


