《2025年一遍过九年级初中数学上册北师大版》

8 [2024 郴州二模] 路灯下,小强对小华说:“我可以踩到你的影子.”从而可以断定他们在路灯的 (A)
A. 同侧
B. 异侧
C. 同侧或异侧
D. 以上答案都不正确

答案： A

9 [2024 枣庄市中区月考] 如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,在灯光照射下,正方形纸板在地面上形成的影子的形状可以是 ( )

答案：
D 由题意知，正方形纸板越靠近光源的边，影子越长。如图，由于正方形纸板有一条对角线与地面垂直，且该对角线与灯所确定的平面垂直于纸板，故AB，AD的影子长度相等，CB，CD的影子长度相等，且AB的影子比CB的影子长。

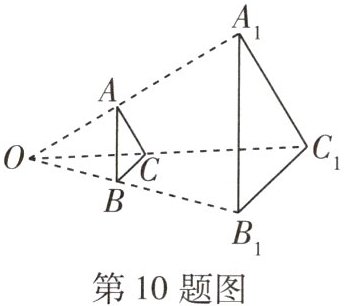
10 [2024 凉山州中考] 如图,一块面积为$ 60 cm^2 $的三角形硬纸板(记为 △ABC)平行于投影面时,在点光源 O 的照射下形成的投影是$ △A_1B_1C_1,$若$ OB:BB_1 = 2:3,$则$ △A_1B_1C_1 $的面积是 (D)
A. 90 cm²
B. 135 cm²
C. 150 cm²
D. 375 cm²

答案： 由题意可知，△ABC∽△A₁B₁C₁，相似比为$\frac{2}{2 + 3}=\frac{2}{5}$，所以$\frac{60}{S_{\triangle A_1B_1C_1}} = (\frac{2}{5})^2$，所以$S_{\triangle A_1B_1C_1} = 375cm^2$。

11 [2025 西安新城区期中] 如图,在平面直角坐标系中,点光源位于点 P(2,2)处,木杆 AB // x 轴,点 A 的坐标为(0,1),木杆 AB 在 x 轴上的投影长度为 6,则点 B 的坐标为 ( )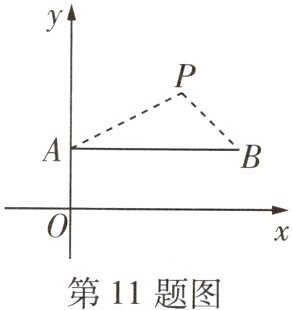
A. (2,1)
B. (3,1)
C. (4,1)
D. (5,1)

答案：
B 如图，延长PA，PB分别交x轴于点A'，点B'，作PE⊥x轴于点E，交AB于点D，
∵P(2,2)，A(0,1)，AB//x轴，
∴PD = 1，PE = 2，A'B' = 6，由AB//A'B'，易得△PAB∽△PA'B'，
∴$\frac{AB}{A'B'} = \frac{PD}{PE}$，即$\frac{AB}{6} = \frac{1}{2}$，
∴AB = 3，
∵点A的坐标为(0,1)，
∴B(3,1)。

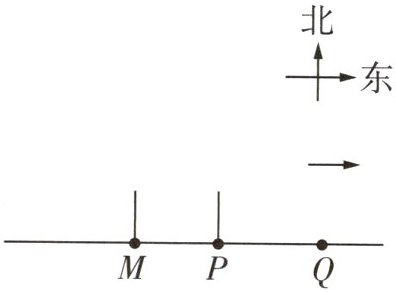
12 [2024 汉中期末] 如图,身高 1.6 m 的小王晚上沿箭头方向散步至一路灯下,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部向东走 20 m 到 M 处,发现自己的影子端点刚好在两盏路灯的中间点 P 处,继续向东走 5 m 到 P 处,此时影子的端点在 Q 处.
(1) 找出路灯灯泡的位置;
(2) 估计路灯的高,并求影长 PQ.

答案：
解：
(1)如图，点O为路灯灯泡的位置。

(2)如图，作OA垂直于地面于点A，AM = 20m，MP = 5m，MN = PB = 1.6m。
由MN//OA，易得△PMN∽△PAO，
∴$\frac{MN}{AO} = \frac{PM}{PA}$，即$\frac{1.6}{AO} = \frac{5}{5 + 20}$，
∴AO = 8m。
由PB//OA，易得△QPB∽△QAO，
∴$\frac{PB}{AO} = \frac{PQ}{AQ}$，即$\frac{1.6}{8} = \frac{PQ}{PQ + 25}$，
∴PQ = $\frac{25}{4}$m。
答：路灯的高为8m，影长PQ为$\frac{25}{4}$m。
策略点拨
确定中心投影点光源的位置的方法
分别连接两个物体的影子顶端及物体上的对应点，作出两条直线，这两条直线的交点就是点光源的位置。理解“点光源发出的任何两条光线相交于一点”即可解题。

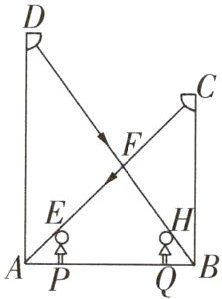
13 [2024 济南长清三中月考] 如图,晚上小明由路灯 AD 走向路灯 BC,当他行至点 P 处时,发现他在路灯 BC 下的影长为 2 m,且影子的顶端恰好在 A 点,接着他又走了 6.5 m 至点 Q 处,此时他在路灯 AD 下的影子的顶端恰好在 B 点,已知小明的身高为 1.8 m,路灯 BC 的高度为 9 m.
(1) 计算小明站在点 Q 处时在路灯 AD 下影子的长度为1.5m;
(2) 计算路灯 AD 的高度为12m.

答案： 解题思路：由路灯、小明都垂直于地面，知AD//PE//QH//BC，用相似三角形中的比例线段可求解。
解：
(1)根据题图，得EP⊥AB，CB⊥AB，
∴EP//CB，易得△AEP∽△ACB，
∴$\frac{EP}{CB} = \frac{AP}{AB}$，即$\frac{1.8}{9} = \frac{2}{AB}$，
∴AB = 10m，
∴QB = AB - AP - PQ = 10 - 2 - 6.5 = 1.5(m)。
即小明站在点Q处时在路灯AD下影子的长度为1.5m。
(2)同
(1)易得△HQB∽△DAB，
∴$\frac{HQ}{DA} = \frac{QB}{AB}$，即$\frac{1.8}{DA} = \frac{1.5}{10}$，
∴AD = 12m。
即路灯AD的高度为12m。

14 推理能力 在长、宽都为 4 m,高为 3 m 的房间的正中央的

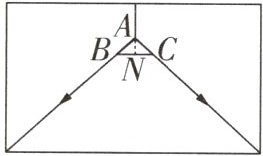
天花板上悬挂一个灯泡,为了集中光线,加上了灯罩,示意图如图所示. 已知灯罩深 AN = 8 cm,灯泡 A 离地面 2 m,为了使光线恰好照到墙角,则灯罩的直径 BC 约为____.(结果精确到 0.01 m,√2 ≈ 1.414)

答案：
0.23m 如图，由于光线要恰好照到墙角，因此点A，B，D和点A，C，E分别在同一条直线上。
∵房间的长、宽都为4m，
∴DE = $4\sqrt{2}$m。(由于光线要照到墙角，则DE的长应为房间底面的对角线长)延长AN交DE于点M，易知AM⊥DE。
由DE//BC，易得△ABC∽△ADE，
∴$\frac{AN}{AM} = \frac{BC}{DE}$。
∵AN = 0.08m，(注意单位要统一)AM = 2m，DE = $4\sqrt{2}$m，
∴BC = $\frac{4\sqrt{2}×0.08}{2}≈0.23(m)$。
∴灯罩的直径BC应约为0.23m。