第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
1 [2025 济南市中区期中]小明要用如图所示的两个转盘做“配紫色(红色和蓝色在一起能配成紫色)”游戏,每个转盘均被等分成若干个扇形,他同时转动两个转盘,停止时指针所指的颜色恰好能配成紫色的概率为 (

A. $\frac{1}{6}$
B. $\frac{1}{4}$
C. $\frac{1}{3}$
D. $\frac{1}{2}$
$\frac{1}{3}$
)
A. $\frac{1}{6}$
B. $\frac{1}{4}$
C. $\frac{1}{3}$
D. $\frac{1}{2}$
答案:
1 C 列表如下:
|第1个\第2个|白|蓝|红|
|----|----|----|----|
|红|(红,白)|(红,蓝)|(红,红)|
|蓝|(蓝,白)|(蓝,蓝)|(蓝,红)|
由表格可知,共有6种等可能的结果,其中有2种结果可以配成紫色,所以恰好能配成紫色的概率是$\frac{2}{6}=\frac{1}{3}$。
|第1个\第2个|白|蓝|红|
|----|----|----|----|
|红|(红,白)|(红,蓝)|(红,红)|
|蓝|(蓝,白)|(蓝,蓝)|(蓝,红)|
由表格可知,共有6种等可能的结果,其中有2种结果可以配成紫色,所以恰好能配成紫色的概率是$\frac{2}{6}=\frac{1}{3}$。
2 [2025 佛山狮山实验学校调研]如图,同时自由转动转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,则可配成紫色的概率是

______.

______.
答案:
2 $\frac{1}{4}$ 将第2个转盘中的红色部分平均分成两部分,记为红1,红2,画树状图如下:

由树状图可知,共有12种等可能的结果,其中红色与蓝色可配成紫色的结果有3种,所以可配成紫色的概率是$\frac{3}{12}=\frac{1}{4}$。
策略点拨
求“非等可能”事件的概率的思路
利用等可能事件的概率公式计算事件的概率,需建立在所有出现的结果都是等可能的基础上,利用列表法或画树状图法求解。当转盘被分割成面积不等的扇形时,通常需要将其转化成等面积的扇形求解。
2 $\frac{1}{4}$ 将第2个转盘中的红色部分平均分成两部分,记为红1,红2,画树状图如下:

由树状图可知,共有12种等可能的结果,其中红色与蓝色可配成紫色的结果有3种,所以可配成紫色的概率是$\frac{3}{12}=\frac{1}{4}$。
策略点拨
求“非等可能”事件的概率的思路
利用等可能事件的概率公式计算事件的概率,需建立在所有出现的结果都是等可能的基础上,利用列表法或画树状图法求解。当转盘被分割成面积不等的扇形时,通常需要将其转化成等面积的扇形求解。
3 [2024 丹东期中]小明和小亮用如图所示的两个可以自由转动的转盘做“配紫色”游戏,同时随机转动两个转盘,若配成紫色,则小明胜,否则小亮胜,这个游戏对双方公平吗?请用列表法或画树状图法说明理由.


答案:
3 解:不公平。理由如下:
将A盘中蓝色部分等分为2份,分别记为蓝a,蓝b,红色部分记为红c,B盘中红色部分等分为2份,分别记为红1,红2,蓝色部分记为蓝3。
画树状图如下:

由树状图可知,共有9种等可能的结果,其中能配成紫色的结果有5种,
∴小明获胜的概率为$\frac{5}{9}$,小亮获胜的概率为$\frac{4}{9}$。
∵$\frac{5}{9}≠\frac{4}{9}$,
∴这个游戏对双方不公平。
3 解:不公平。理由如下:
将A盘中蓝色部分等分为2份,分别记为蓝a,蓝b,红色部分记为红c,B盘中红色部分等分为2份,分别记为红1,红2,蓝色部分记为蓝3。
画树状图如下:

由树状图可知,共有9种等可能的结果,其中能配成紫色的结果有5种,
∴小明获胜的概率为$\frac{5}{9}$,小亮获胜的概率为$\frac{4}{9}$。
∵$\frac{5}{9}≠\frac{4}{9}$,
∴这个游戏对双方不公平。
4 创新意识 教材 P68T4 变式 如图,三个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色. 小强和小亮用转盘 A 和转盘 B 做一个转盘游戏:同时转动两个转盘,若其中一个转出红色,另一个转出蓝色即可配成紫色,则小强获胜;若两个转盘转出的颜色相同,则小亮获胜;在其他情况下,小强和小亮不分胜负.
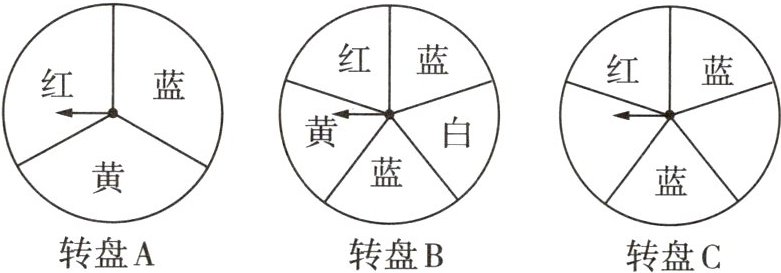
(1)用画树状图或列表的方法表示此游戏所有可能出现的结果;
(2)小强认为此游戏不公平,请你帮他说明理由;
(3)请你在转盘 C 的空白处,涂上适当颜色,使得用转盘 C 替换转盘 B 后,游戏对小强和小亮是公平的(在空白处填写表示颜色的文字即可,不要求说明理由,只需给出一种结果即可).

(1)用画树状图或列表的方法表示此游戏所有可能出现的结果;
(2)小强认为此游戏不公平,请你帮他说明理由;
(3)请你在转盘 C 的空白处,涂上适当颜色,使得用转盘 C 替换转盘 B 后,游戏对小强和小亮是公平的(在空白处填写表示颜色的文字即可,不要求说明理由,只需给出一种结果即可).
答案:
4 解:
(1)列表如下:
|转盘A\转盘B|红|蓝|白|蓝|黄|
|----|----|----|----|----|----|
|红|(红,红)|(红,蓝)|(红,白)|(红,蓝)|(红,黄)|
|蓝|(蓝,红)|(蓝,蓝)|(蓝,白)|(蓝,蓝)|(蓝,黄)|
|黄|(黄,红)|(黄,蓝)|(黄,白)|(黄,蓝)|(黄,黄)|
(2)由
(1)中表格可知,共有15种等可能的结果,能配成紫色的结果有3种,两个转盘转出的颜色相同的结果有4种,
∴$P$(小强获胜)$=\frac{3}{15}=\frac{1}{5}$,$P$(小亮获胜)$=\frac{4}{15}$。
∵$P$(小强获胜)$≠P$(小亮获胜),
∴此游戏不公平。
(3)如图,此时$P$(小强获胜)$=P$(小亮获胜)$=\frac{1}{5}$,则游戏对小强和小亮是公平的。(答案不唯一,正确即可)

4 解:
(1)列表如下:
|转盘A\转盘B|红|蓝|白|蓝|黄|
|----|----|----|----|----|----|
|红|(红,红)|(红,蓝)|(红,白)|(红,蓝)|(红,黄)|
|蓝|(蓝,红)|(蓝,蓝)|(蓝,白)|(蓝,蓝)|(蓝,黄)|
|黄|(黄,红)|(黄,蓝)|(黄,白)|(黄,蓝)|(黄,黄)|
(2)由
(1)中表格可知,共有15种等可能的结果,能配成紫色的结果有3种,两个转盘转出的颜色相同的结果有4种,
∴$P$(小强获胜)$=\frac{3}{15}=\frac{1}{5}$,$P$(小亮获胜)$=\frac{4}{15}$。
∵$P$(小强获胜)$≠P$(小亮获胜),
∴此游戏不公平。
(3)如图,此时$P$(小强获胜)$=P$(小亮获胜)$=\frac{1}{5}$,则游戏对小强和小亮是公平的。(答案不唯一,正确即可)

查看更多完整答案,请扫码查看


