第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
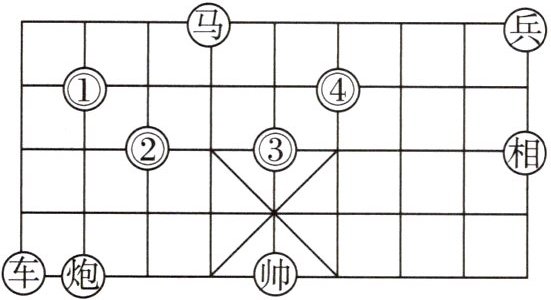
8 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,使“马”“车”“炮”所在位置的格点构成的三角形与“帅”“相”“兵”所在位置的格点构成的三角形相似,“马”应落在 (
A. ①处
B. ②处
C. ③处
D. ④处
B
)
A. ①处
B. ②处
C. ③处
D. ④处
答案:
B 设小正方形的边长为1,由“帅”“相”“兵”所在位置的格点构成的三角形的三边的长分别为2,$2\sqrt{5}$,$4\sqrt{2}$;“车”“炮”所在位置的格点之间的距离为1,“炮”“②”所在位置的格点之间的距离为$\sqrt{5}$,“车”“②”所在位置的格点之间的距离为$2\sqrt{2}$,因为$\frac{\sqrt{5}}{2\sqrt{5}}=\frac{2\sqrt{2}}{4\sqrt{2}}=\frac{1}{2}$,所以“马”应落在②处.
9 [2024 北京石景山区期中] 如图,四边形 ABCD,CDEF,EFGH 都是正方形,则∠1 + ∠2 的度数为

$45^{\circ}$
.
答案:
$45^{\circ}$ 设正方形$ABCD$的边长为$a$,则$AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{2}a$,$AF=\sqrt{AB^{2}+BF^{2}}=\sqrt{5}a$,$AG=\sqrt{AB^{2}+BG^{2}}=\sqrt{10}a$.$\because\frac{AC}{CF}=\frac{\sqrt{2}a}{a}=\sqrt{2}$,$\frac{CG}{AC}=\frac{2a}{\sqrt{2}a}=\sqrt{2}$,$\frac{AG}{AF}=\frac{\sqrt{10}a}{\sqrt{5}a}=\sqrt{2}$,$\therefore\frac{AC}{FC}=\frac{CG}{CA}=\frac{AG}{FA}$,$\therefore\triangle GCA\backsim\triangle ACF$,(也可利用判定定理2来判定)$\therefore\angle 1=\angle CAF$.$\because\angle ACB=\angle CAF+\angle 2=45^{\circ}$,$\therefore\angle 1+\angle 2=45^{\circ}$.
10 [2024 南京金陵中学月考] 如图,已知$\frac {AB}{BD}= \frac {BC}{BE}= \frac {AC}{DE}$.
(1) 证明:∠ABD = ∠CBE.
证明:
(2) ∠BAD 与∠BCE 相等吗? 为什么?
解:∠BAD与∠BCE
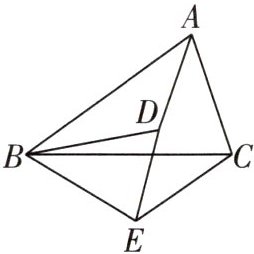
(1) 证明:∠ABD = ∠CBE.
证明:
$\because\frac{AB}{BD}=\frac{BC}{BE}=\frac{AC}{DE}$,$\therefore\triangle ABC\backsim\triangle DBE$,$\therefore\angle ABC=\angle DBE$,$\therefore\angle ABC-\angle DBC=\angle DBE-\angle DBC$,$\therefore\angle ABD=\angle CBE$.
(2) ∠BAD 与∠BCE 相等吗? 为什么?
解:∠BAD与∠BCE
相等
.理由如下:$\because\frac{AB}{BD}=\frac{BC}{BE}$,$\angle ABD=\angle CBE$,$\therefore\frac{AB}{CB}=\frac{BD}{BE}$,$\therefore\triangle ABD\backsim\triangle CBE$,$\therefore\angle BAD=\angle BCE$.

答案:
(1)证明:$\because\frac{AB}{BD}=\frac{BC}{BE}=\frac{AC}{DE}$,$\therefore\triangle ABC\backsim\triangle DBE$,$\therefore\angle ABC=\angle DBE$,$\therefore\angle ABC-\angle DBC=\angle DBE-\angle DBC$,$\therefore\angle ABD=\angle CBE$.
(2)解:$\angle BAD=\angle BCE$.理由如下:
$\because\frac{AB}{BD}=\frac{BC}{BE}$,$\angle ABD=\angle CBE$,$\therefore\frac{AB}{CB}=\frac{BD}{BE}$,$\therefore\triangle ABD\backsim\triangle CBE$,$\therefore\angle BAD=\angle BCE$.
(1)证明:$\because\frac{AB}{BD}=\frac{BC}{BE}=\frac{AC}{DE}$,$\therefore\triangle ABC\backsim\triangle DBE$,$\therefore\angle ABC=\angle DBE$,$\therefore\angle ABC-\angle DBC=\angle DBE-\angle DBC$,$\therefore\angle ABD=\angle CBE$.
(2)解:$\angle BAD=\angle BCE$.理由如下:
$\because\frac{AB}{BD}=\frac{BC}{BE}$,$\angle ABD=\angle CBE$,$\therefore\frac{AB}{CB}=\frac{BD}{BE}$,$\therefore\triangle ABD\backsim\triangle CBE$,$\therefore\angle BAD=\angle BCE$.
11 几何直观 新趋势·过程性学习 [2025 德州期中] 如图,在△ABC 和△A'B'C'中,点 D,D'分别是 AB,A'B'上的一点,$\frac {AD}{AB}= \frac {A'D'}{A'B'}$.
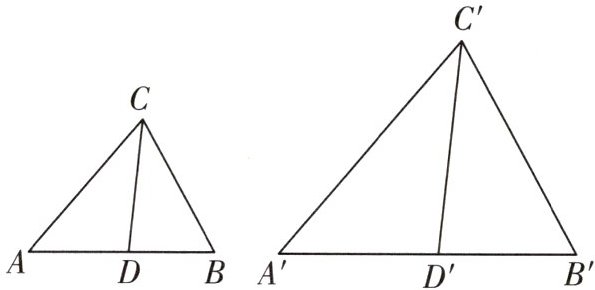
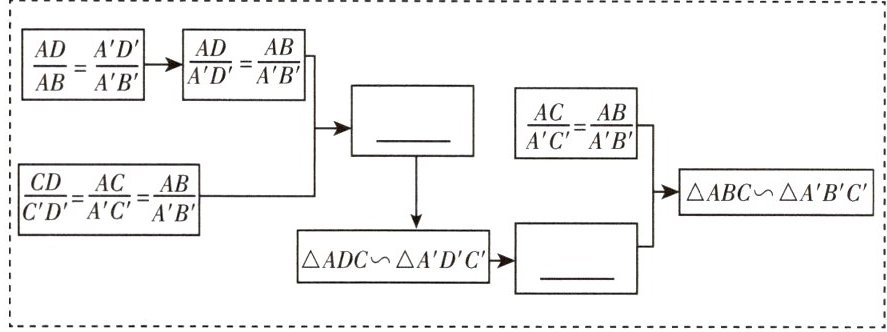
(1) 当$\frac {CD}{C'D'}= \frac {AC}{A'C'}= \frac {AB}{A'B'}$时,求证:△ABC∽△A'B'C'.
证明的途径可以用下面的框图表示,请填写其中的空格.
(2) 当$\frac {CD}{C'D'}= \frac {AC}{A'C'}= \frac {BC}{B'C'}$时,判断△ABC 与△A'B'C'是否相似,并说明理由.
【回顾与思考】
判定两个三角形相似的条件有哪些?

(1) 当$\frac {CD}{C'D'}= \frac {AC}{A'C'}= \frac {AB}{A'B'}$时,求证:△ABC∽△A'B'C'.
证明的途径可以用下面的框图表示,请填写其中的空格.

(2) 当$\frac {CD}{C'D'}= \frac {AC}{A'C'}= \frac {BC}{B'C'}$时,判断△ABC 与△A'B'C'是否相似,并说明理由.
【回顾与思考】
判定两个三角形相似的条件有哪些?
答案:
(1)$\frac{CD}{C'D'}=\frac{AC}{A'C'}=\frac{AD}{A'D'}$ $\angle A=\angle A'$
(2)相似.理由如下:
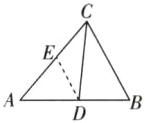
如图,分别过点$D,D'$作$DE// BC$,$D'E'// B'C'$,$DE$交$AC$于点$E$,$D'E'$交$A'C'$于点$E'$.
由$DE// BC$,易得$\triangle ADE\backsim\triangle ABC$,$\therefore\frac{AD}{AB}=\frac{DE}{BC}=\frac{AE}{AC}$,
同理$\frac{A'D'}{A'B'}=\frac{D'E'}{B'C'}=\frac{A'E'}{A'C'}$,
又$\because\frac{AD}{AB}=\frac{A'D'}{A'B'}$,$\therefore\frac{DE}{BC}=\frac{D'E'}{B'C'}$,$\frac{AE}{AC}=\frac{A'E'}{A'C'}$,$\therefore\frac{DE}{D'E'}=\frac{BC}{B'C'}$,$\frac{AC - AE}{AC}=\frac{A'C' - A'E'}{A'C'}$,$\therefore\frac{EC}{AC}=\frac{E'C'}{A'C'}$,$\therefore\frac{EC}{E'C'}=\frac{AC}{A'C'}$,
又$\because\frac{CD}{C'D'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}$,$\therefore\frac{CD}{C'D'}=\frac{EC}{E'C'}=\frac{DE}{D'E'}$,$\therefore\triangle DCE\backsim\triangle D'C'E'$,$\therefore\angle CED=\angle C'E'D'$.
$\because DE// BC$,$\therefore\angle CED+\angle ACB=180^{\circ}$.
同理$\angle C'E'D'+\angle A'C'B'=180^{\circ}$,$\therefore\angle ACB=\angle A'C'B'$,
又$\because\frac{AC}{A'C'}=\frac{BC}{B'C'}$,$\therefore\triangle ABC\backsim\triangle A'B'C'$.

(1)$\frac{CD}{C'D'}=\frac{AC}{A'C'}=\frac{AD}{A'D'}$ $\angle A=\angle A'$
(2)相似.理由如下:
如图,分别过点$D,D'$作$DE// BC$,$D'E'// B'C'$,$DE$交$AC$于点$E$,$D'E'$交$A'C'$于点$E'$.
由$DE// BC$,易得$\triangle ADE\backsim\triangle ABC$,$\therefore\frac{AD}{AB}=\frac{DE}{BC}=\frac{AE}{AC}$,
同理$\frac{A'D'}{A'B'}=\frac{D'E'}{B'C'}=\frac{A'E'}{A'C'}$,
又$\because\frac{AD}{AB}=\frac{A'D'}{A'B'}$,$\therefore\frac{DE}{BC}=\frac{D'E'}{B'C'}$,$\frac{AE}{AC}=\frac{A'E'}{A'C'}$,$\therefore\frac{DE}{D'E'}=\frac{BC}{B'C'}$,$\frac{AC - AE}{AC}=\frac{A'C' - A'E'}{A'C'}$,$\therefore\frac{EC}{AC}=\frac{E'C'}{A'C'}$,$\therefore\frac{EC}{E'C'}=\frac{AC}{A'C'}$,
又$\because\frac{CD}{C'D'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}$,$\therefore\frac{CD}{C'D'}=\frac{EC}{E'C'}=\frac{DE}{D'E'}$,$\therefore\triangle DCE\backsim\triangle D'C'E'$,$\therefore\angle CED=\angle C'E'D'$.
$\because DE// BC$,$\therefore\angle CED+\angle ACB=180^{\circ}$.
同理$\angle C'E'D'+\angle A'C'B'=180^{\circ}$,$\therefore\angle ACB=\angle A'C'B'$,
又$\because\frac{AC}{A'C'}=\frac{BC}{B'C'}$,$\therefore\triangle ABC\backsim\triangle A'B'C'$.


查看更多完整答案,请扫码查看


