第21页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
1 阅读下列材料:
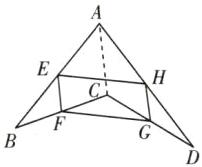
如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来,得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.
点E,F分别是AB,BC的中点$\xrightarrow{三角形中位线定理}EF// AC,$$EF= \frac{1}{2}AC;$
点H,G分别是AD,CD的中点$\xrightarrow{三角形中位线定理}HG// AC,$$HG= \frac{1}{2}AC→EF// HG,$EF= HG→四边形EFGH是平行四边形.
结合小敏的思路作答:
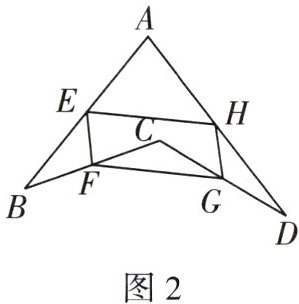
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?请说明理由.
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形?写出结论并证明.
②当AC与BD满足什么条件时,四边形EFGH是矩形?直接写出结论即可.

如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来,得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.
点E,F分别是AB,BC的中点$\xrightarrow{三角形中位线定理}EF// AC,$$EF= \frac{1}{2}AC;$
点H,G分别是AD,CD的中点$\xrightarrow{三角形中位线定理}HG// AC,$$HG= \frac{1}{2}AC→EF// HG,$EF= HG→四边形EFGH是平行四边形.
结合小敏的思路作答:
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?请说明理由.
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形?写出结论并证明.
②当AC与BD满足什么条件时,四边形EFGH是矩形?直接写出结论即可.


答案:
解:
(1)四边形EFGH是平行四边形.理由如下:
如图,连接AC,
∵E是AB的中点,F是BC的中点,
∴EF//AC,EF=$\frac{1}{2}$AC,
同理,HG//AC,HG=$\frac{1}{2}$AC,
疑难集训
∴EF//HG,EF=HG,
∴四边形EFGH是平行四边形.
(2)①当AC=BD时,四边形EFGH为菱形.证明如下:
由
(1)得,四边形EFGH是平行四边形,HG=$\frac{1}{2}$AC,
∵F,G分别是BC,CD的中点,
∴FG=$\frac{1}{2}$BD,
当AC=BD时,FG=HG,
∴四边形EFGH为菱形.
②当AC⊥BD时,四边形EFGH为矩形.
提示:同
(1)得,四边形EFGH是平行四边形,
∵AC⊥BD,GH//AC,
∴GH⊥BD.
∵F,G分别是BC,CD的中点,
∴GF//BD,
∴GH⊥GF,
∴∠HGF=90°,
∴四边形EFGH为矩形.
解:
(1)四边形EFGH是平行四边形.理由如下:
如图,连接AC,
∵E是AB的中点,F是BC的中点,
∴EF//AC,EF=$\frac{1}{2}$AC,

同理,HG//AC,HG=$\frac{1}{2}$AC,
疑难集训
∴EF//HG,EF=HG,
∴四边形EFGH是平行四边形.
(2)①当AC=BD时,四边形EFGH为菱形.证明如下:
由
(1)得,四边形EFGH是平行四边形,HG=$\frac{1}{2}$AC,
∵F,G分别是BC,CD的中点,
∴FG=$\frac{1}{2}$BD,
当AC=BD时,FG=HG,
∴四边形EFGH为菱形.
②当AC⊥BD时,四边形EFGH为矩形.
提示:同
(1)得,四边形EFGH是平行四边形,
∵AC⊥BD,GH//AC,
∴GH⊥BD.
∵F,G分别是BC,CD的中点,
∴GF//BD,
∴GH⊥GF,
∴∠HGF=90°,
∴四边形EFGH为矩形.
2 [2025驻马店十中期中]如图,在边长为4的正方形ABCD中,点E,F分别是边BC,CD上的动点,且BE= CF,连接BF,DE,则BF+DE的最小值为( )
$A. 2\sqrt{3} B. 2\sqrt{5} C. 4\sqrt{3} D. 4\sqrt{5}$

$A. 2\sqrt{3} B. 2\sqrt{5} C. 4\sqrt{3} D. 4\sqrt{5}$

答案:
D 如图1,连接AE.
∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCF=90°,又
∵BE=CF,
∴△ABE≌△BCF,
∴AE=BF,
∴BF+DE=AE+DE.延长AB到点H,使得BH=AB,连接EH,DH,则EH=AE,
∴AE+DE=EH+DE≥DH.如图2,当D,E,H三点共线时,AE+DE取最小值,此时AE+DE=DH.在Rt△ADH中,DH=$\sqrt{AH^{2}+AD^{2}}=\sqrt{8^{2}+4^{2}}=4\sqrt{5}$,
∴BF+DE的最小值为$4\sqrt{5}$.
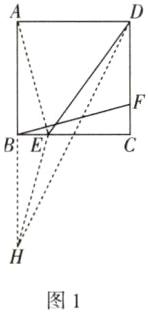

D 如图1,连接AE.
∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCF=90°,又
∵BE=CF,
∴△ABE≌△BCF,
∴AE=BF,
∴BF+DE=AE+DE.延长AB到点H,使得BH=AB,连接EH,DH,则EH=AE,
∴AE+DE=EH+DE≥DH.如图2,当D,E,H三点共线时,AE+DE取最小值,此时AE+DE=DH.在Rt△ADH中,DH=$\sqrt{AH^{2}+AD^{2}}=\sqrt{8^{2}+4^{2}}=4\sqrt{5}$,
∴BF+DE的最小值为$4\sqrt{5}$.


3 [2025晋中段考]如图,四边形ABCD是边长为1的正方形,分别延长BD,DB至点E,F,使$BF= DE= \sqrt{2}.$连接AE,AF,CE,CF.
(1)求证:四边形AECF是菱形.
(2)求四边形AECF的面积.
(3)如果M为AF的中点,P为线段EF上的一动点,求PA+PM的最小值.

(1)求证:四边形AECF是菱形.
(2)求四边形AECF的面积.
(3)如果M为AF的中点,P为线段EF上的一动点,求PA+PM的最小值.

答案:
(1)证明:如图,连接AC,交BD于点O,
∵四边形ABCD是正方形,
∴BD⊥AC,BO=DO,AO=CO.
∵BF=DE,
∴OD+DE=OB+BF,即OE=OF,
∴四边形AECF是平行四边形,
又
∵EF⊥AC,
∴四边形AECF是菱形.
(2)解:
∵四边形ABCD是边长为1的正方形,
∴AB=AD=1,
∴BD=AC=$\sqrt{2}$,
∴EF=3$\sqrt{2}$,
∴四边形AECF的面积为$\frac{1}{2}$AC·EF=$\frac{1}{2}$×$\sqrt{2}$×3$\sqrt{2}$=3.
(3)解:
∵四边形AECF是菱形,
∴点A与点C关于直线EF对称.
由
(2)知EF=3$\sqrt{2}$,AC=$\sqrt{2}$,
∴OF=$\frac{1}{2}$EF=$\frac{3\sqrt{2}}{2}$,OC=$\frac{1}{2}$AC=$\frac{\sqrt{2}}{2}$.
在Rt△OCF中,CF=$\sqrt{OC^{2}+OF^{2}}=\sqrt{5}$.
如图,连接CM,交EF于点P,连接PA.此时PA+PM的值最小(当C,P,M三点不共线时,PC+PM>CM),最小值等于CM的长,
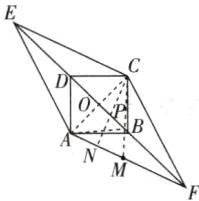
过C作CN⊥AF于N,则AC²−AN²=CN²=CF²−NF².
设AN=x,
∴($\sqrt{2}$)²−x²=($\sqrt{5}$)²−($\sqrt{5}$−x)²,
解得x=$\frac{\sqrt{5}}{5}$,
∴MN=$\frac{1}{2}$AF−AN=$\frac{3\sqrt{5}}{10}$,
∵CM²−MN²=AC²−AN²,
∴CM²−($\frac{3\sqrt{5}}{10}$)²=($\sqrt{2}$)²−($\frac{\sqrt{5}}{5}$)²,
∴CM=$\frac{3}{2}$,
故PA+PM的最小值为$\frac{3}{2}$.
(1)证明:如图,连接AC,交BD于点O,
∵四边形ABCD是正方形,
∴BD⊥AC,BO=DO,AO=CO.
∵BF=DE,
∴OD+DE=OB+BF,即OE=OF,
∴四边形AECF是平行四边形,
又
∵EF⊥AC,
∴四边形AECF是菱形.
(2)解:
∵四边形ABCD是边长为1的正方形,
∴AB=AD=1,
∴BD=AC=$\sqrt{2}$,
∴EF=3$\sqrt{2}$,
∴四边形AECF的面积为$\frac{1}{2}$AC·EF=$\frac{1}{2}$×$\sqrt{2}$×3$\sqrt{2}$=3.
(3)解:
∵四边形AECF是菱形,
∴点A与点C关于直线EF对称.
由
(2)知EF=3$\sqrt{2}$,AC=$\sqrt{2}$,
∴OF=$\frac{1}{2}$EF=$\frac{3\sqrt{2}}{2}$,OC=$\frac{1}{2}$AC=$\frac{\sqrt{2}}{2}$.
在Rt△OCF中,CF=$\sqrt{OC^{2}+OF^{2}}=\sqrt{5}$.
如图,连接CM,交EF于点P,连接PA.此时PA+PM的值最小(当C,P,M三点不共线时,PC+PM>CM),最小值等于CM的长,

过C作CN⊥AF于N,则AC²−AN²=CN²=CF²−NF².
设AN=x,
∴($\sqrt{2}$)²−x²=($\sqrt{5}$)²−($\sqrt{5}$−x)²,
解得x=$\frac{\sqrt{5}}{5}$,
∴MN=$\frac{1}{2}$AF−AN=$\frac{3\sqrt{5}}{10}$,
∵CM²−MN²=AC²−AN²,
∴CM²−($\frac{3\sqrt{5}}{10}$)²=($\sqrt{2}$)²−($\frac{\sqrt{5}}{5}$)²,
∴CM=$\frac{3}{2}$,
故PA+PM的最小值为$\frac{3}{2}$.
查看更多完整答案,请扫码查看


