第89页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
1 [2024宁德期中]下列图形中,$\triangle ABC\backsim\triangle DEF$,其中$\triangle ABC和\triangle DEF$不是位似图形的是(

B
)
答案:
B
归纳总结
相似与位似的区别与联系
(1)相似仅要求两个图形的形状完全相同,而位似是在相似的基础上要求对应点的连线或延长线相交于一点,且满足定义中的“$OP'=k\cdot OP(k≠0)$”。
(2)如果两个图形是位似图形,那么这两个图形一定是相似图形;反之,则不一定成立。
归纳总结
相似与位似的区别与联系
(1)相似仅要求两个图形的形状完全相同,而位似是在相似的基础上要求对应点的连线或延长线相交于一点,且满足定义中的“$OP'=k\cdot OP(k≠0)$”。
(2)如果两个图形是位似图形,那么这两个图形一定是相似图形;反之,则不一定成立。
2 [2025天津和平区期中]如图,$\triangle ABC与\triangle A'B'C'$是位似图形,则位似中心为点______.


答案:
P 如图,连接$AA'$,$BB'$,$CC'$,根据位似图形对应点的连线的交点是位似中心,可知点P是位似中心。

P 如图,连接$AA'$,$BB'$,$CC'$,根据位似图形对应点的连线的交点是位似中心,可知点P是位似中心。

3 指出下列各图中的两个图形是不是位似图形,如果是位似图形,请指出其位似中心.
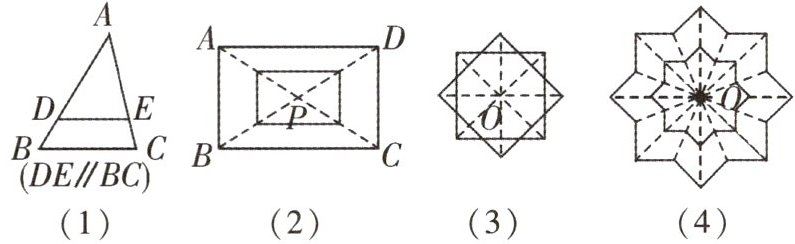
(1)是位似图形,位似中心是点
归纳总结
位似图形必须同时满足的三个条件
(1)两个图形是相似图形;(2)两个相似图形的每组对应顶点所在的直线都经过同一点;(3)定义中的“

(1)是位似图形,位似中心是点
A
;(2)是位似图形,位似中心是点P
;(3)不是
位似图形;(4)是位似图形,位似中心是点O
。归纳总结
位似图形必须同时满足的三个条件
(1)两个图形是相似图形;(2)两个相似图形的每组对应顶点所在的直线都经过同一点;(3)定义中的“
$OP'=k\cdot OP(k≠0)$
”。
答案:
解:
(1)、
(2)和
(4)中的两个图形都是位似图形,
(3)中的两个图形不是位似图形,
(1)中的位似中心是点A,
(2)中的位似中心是点P,
(4)中的位似中心是点O。
归纳总结
位似图形必须同时满足的三个条件
(1)两个图形是相似图形;
(2)两个相似图形的每组对应顶点所在的直线都经过同一点;
(3)定义中的“$OP'=k\cdot OP(k≠0)$”。
(1)、
(2)和
(4)中的两个图形都是位似图形,
(3)中的两个图形不是位似图形,
(1)中的位似中心是点A,
(2)中的位似中心是点P,
(4)中的位似中心是点O。
归纳总结
位似图形必须同时满足的三个条件
(1)两个图形是相似图形;
(2)两个相似图形的每组对应顶点所在的直线都经过同一点;
(3)定义中的“$OP'=k\cdot OP(k≠0)$”。
4 [2024衡阳期末]如图,四边形$ABCD和四边形A'B'C'D'$是位似图形,点$O$为位似中心,且相似比为$5:3$,若四边形$A'B'C'D'$的面积为9cm²,则四边形$ABCD$的面积为(
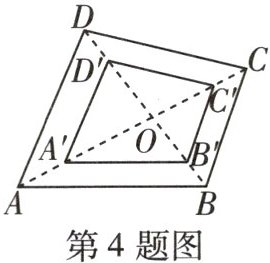
A. $15cm^{2}$
B. $25cm^{2}$
C. $18cm^{2}$
D. $27cm^{2}$
25cm²
)
A. $15cm^{2}$
B. $25cm^{2}$
C. $18cm^{2}$
D. $27cm^{2}$
答案:
B
∵ 四边形ABCD和四边形$A'B'C'D'$是位似图形,且相似比为$5:3$,
∴$S_{四边形A'B'C'D'}:S_{四边形ABCD}=9:25$,
∵ 四边形$A'B'C'D'$的面积为$9cm^{2}$,
∴ 四边形ABCD的面积为$25cm^{2}$。
∵ 四边形ABCD和四边形$A'B'C'D'$是位似图形,且相似比为$5:3$,
∴$S_{四边形A'B'C'D'}:S_{四边形ABCD}=9:25$,
∵ 四边形$A'B'C'D'$的面积为$9cm^{2}$,
∴ 四边形ABCD的面积为$25cm^{2}$。
5 [2024重庆大渡口区一模]如图,$\triangle ABC与\triangle DEF$位似,点$O$为位似中心,$OD= 2OA$,$BC= 3$,则$EF$的长是(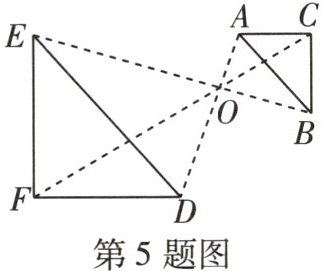
A. 12
B. 10
C. 8
D. 6
D
)
A. 12
B. 10
C. 8
D. 6
答案:
D
6 [2023长春中考]如图,$\triangle ABC和\triangle A'B'C'是以点O$为位似中心的位似图形,点$A在线段OA'$上.若$OA:AA'= 1:2$,则$\triangle ABC与\triangle A'B'C'$的周长之比为______

1:3
.
答案:
$1:3$
∵$OA:AA'=1:2$,
∴$OA:OA'=1:3$,
∴$△ABC$和$△A'B'C'$的相似比为$1:3$,
∴$△ABC$与$△A'B'C'$的周长之比为$1:3$。
∵$OA:AA'=1:2$,
∴$OA:OA'=1:3$,
∴$△ABC$和$△A'B'C'$的相似比为$1:3$,
∴$△ABC$与$△A'B'C'$的周长之比为$1:3$。
7 [2024枣庄市中区月考]如图,以点$O$为位似中心,把$\triangle ABC放大为原图形的2倍得到\triangle A'B'C'$,以下说法正确的是______
①$S_{\triangle ABC}:S_{\triangle A'B'C'}= 1:2$;②$AB:A'B'= 1:2$;③点$A$,$O$,$A'$三点在同一条直线上;④$BC// B'C'$.
②③④
.(填序号)
①$S_{\triangle ABC}:S_{\triangle A'B'C'}= 1:2$;②$AB:A'B'= 1:2$;③点$A$,$O$,$A'$三点在同一条直线上;④$BC// B'C'$.
答案:
②③④ 以点O为位似中心,把$△ABC$放大为原图形的2倍得到$△A'B'C'$,则点$A$,$O$,$A'$三点在同一条直线上,$BC// B'C'$,$△ABC\backsim △A'B'C'$,且相似比为$1:2$,
∴$AB:A'B'=1:2$,$S_{△ABC}:S_{△A'B'C'}=1:4$,故①说法错误,②③④说法正确。
∴$AB:A'B'=1:2$,$S_{△ABC}:S_{△A'B'C'}=1:4$,故①说法错误,②③④说法正确。
8 [2025石家庄外国语学校月考]如图是$6×6$的网格,每个小正方形的边长均为$1$,点$A$,$B$,$C$均在格点上,按下列要求完成作图.
(1)以点$A$为位似中心,将$\triangle ABC放大3倍得到\triangle AB_{1}C_{1}$,请在网格中画出$\triangle AB_{1}C_{1}$;
(2)在线段$B_{1}C_{1}上作点D$,使得$B_{1}D:C_{1}D= 2$.(要求:用无刻度的直尺,保留作图痕迹)
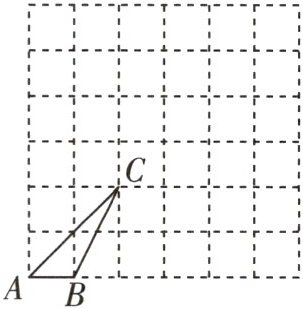
(1)以点$A$为位似中心,将$\triangle ABC放大3倍得到\triangle AB_{1}C_{1}$,请在网格中画出$\triangle AB_{1}C_{1}$;
(2)在线段$B_{1}C_{1}上作点D$,使得$B_{1}D:C_{1}D= 2$.(要求:用无刻度的直尺,保留作图痕迹)

答案:
解:
(1)如图,$△AB_{1}C_{1}$即所求。

(2)如图,取格点M,N,使$B_{1}N:C_{1}M=2$,且$B_{1}N// C_{1}M$,连接MN交$B_{1}C_{1}$于点D,
此时$△B_{1}DN\backsim △C_{1}DM$,
∴$B_{1}D:C_{1}D=B_{1}N:C_{1}M=2$,则点D即所求。
解题通法
画位似图形的一般步骤
(1)确定位似中心;
(2)确定原图形的关键点,通常是多边形的顶点;
(3)分别连接原图形中的关键点和位似中心,并延长(或截取);
(4)根据已知的相似比,确定所画位似图形中关键点的位置;
(5)顺次连接各点,得到放大或缩小后的图形。
解:
(1)如图,$△AB_{1}C_{1}$即所求。

(2)如图,取格点M,N,使$B_{1}N:C_{1}M=2$,且$B_{1}N// C_{1}M$,连接MN交$B_{1}C_{1}$于点D,
此时$△B_{1}DN\backsim △C_{1}DM$,
∴$B_{1}D:C_{1}D=B_{1}N:C_{1}M=2$,则点D即所求。
解题通法
画位似图形的一般步骤
(1)确定位似中心;
(2)确定原图形的关键点,通常是多边形的顶点;
(3)分别连接原图形中的关键点和位似中心,并延长(或截取);
(4)根据已知的相似比,确定所画位似图形中关键点的位置;
(5)顺次连接各点,得到放大或缩小后的图形。
查看更多完整答案,请扫码查看


