《2025年一遍过九年级初中数学上册北师大版》

6 [2024深圳南山区期中]如图,李明用自制的直角三角形纸板去测量“步云阁”的高度,他调整自己的位置,设法使斜边DF保持水平,边DE与点B在同一直线上,已知直角三角形纸板中DE= 16cm,EF= 12cm,测得眼睛D离地面的高度为1.8m,他与“步云阁”的水平距离CD为104m,则“步云阁”的高度AB= ______79.8m.

答案： 79.8 在△DEF和△DCB中,∠D=∠D,∠DEF=∠DCB=90°,
∴△DEF∽△DCB,
∴$\frac{DE}{DC}$=$\frac{EF}{CB}$,
∵DE=16cm=0.16m,EF=12cm=0.12m,DC=104m,
∴$\frac{0.16}{104}$=$\frac{0.12}{CB}$,
∴CB=78m,又
∵AC=1.8m,
∴AB=AC+CB=79.8m.

7 一题多解 [2025亳州期中]小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O,C,D,F,G五点在同一直线上,A,B,O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,求旗杆的高AB.

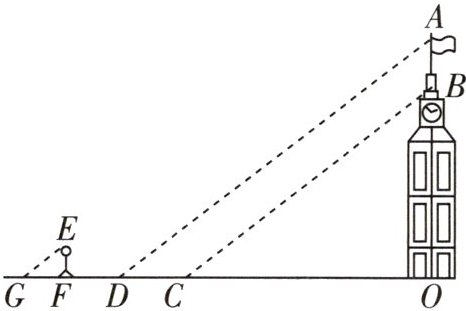
答案：
解:解法一
∵AD//EG,
∴∠ADO=∠EGF,
又
∵∠AOD=∠EFG=90°,
∴△AOD∽△EFG,
∴$\frac{AO}{EF}$=$\frac{OD}{FG}$,即$\frac{AO}{1.8}$=$\frac{20}{2.4}$,
∴AO=15米,
同理,△BOC∽△AOD,
∴$\frac{BO}{AO}$=$\frac{OC}{OD}$,即$\frac{BO}{15}$=$\frac{16}{20}$,
∴BO=12米,
∴AB=AO−BO=15−12=3(米).
答:旗杆的高AB是3米.
解法二 如图,过点C作CM⊥OD于点C,交AD于点M,
∵AD//EG,

∴∠EGF=∠ADO,
又
∵∠EFG=∠MCD=90°,
∴△EGF∽△MDC,
∴$\frac{EF}{MC}$=$\frac{GF}{DC}$,即$\frac{1.8}{MC}$=$\frac{2.4}{20−16}$,
∴MC=3米,
∵MC⊥OD,AB⊥OD
∴MC//AB
又
∵BC//AD,
∴四边形ABCM为平行四边形，
∴AB=MC=3米.
答:旗杆的高AB是3米.