《2025年一遍过九年级初中数学上册北师大版》

1 [2025济南期中]如图,利用标杆DA测量楼高,点C,A,B在同一直线上,DA⊥CB,EB⊥CB,垂足分别为A,B.若测得影长AB= 16米,DA= 3米,影长CA= 4米,则楼高EB为12米.

答案： 12
∵DA⊥CB,EB⊥CB,
∴∠DAC=∠EBA=90°.
∵DC//EA,
∴∠DCA=∠EAB,
∴△DCA∽△EAB,
∴$\frac{DA}{EB}$=$\frac{CA}{AB}$,
∴$\frac{3}{EB}$=$\frac{4}{16}$，解得EB=12米,
∴楼高EB为12米.
归纳总结
利用阳光下的影子测高的原理
同一时刻物高与影长成比例，即相似三角形的对应边成比例。本题中，楼的影子和标杆的影子必须是同一时刻测量得到的，“同一时刻”是应用影子测量物体高度的前提条件，同一时刻的光线互相平行。

2 [2025西安期中]如图,在数学实践活动课上,小辰准备测量一座电视塔的高度.他站在该电视塔的影子上前后移动,直到他自己影子的顶端正好与电视塔的影子的顶端重合(点E处),此时他与该塔的距离BD= 22m.已知电视塔、小辰均与地面BE垂直,且小辰的身高CD= 1.7m,他的影长DE= 2m.该电视塔的高度(AB)为______20.4m.

答案： 20.4m
∵AB⊥BE,CD⊥BE,
∴AB//CD,易得△ABE∽△CDE,(利用“两角分别相等的两个三角形相似”)
∴$\frac{AB}{CD}$=$\frac{BE}{DE}$,
∴$\frac{AB}{CD}$=$\frac{BD+DE}{DE}$,
∴$\frac{AB}{1.7}$=$\frac{22+2}{2}$,
∴AB=20.4m.

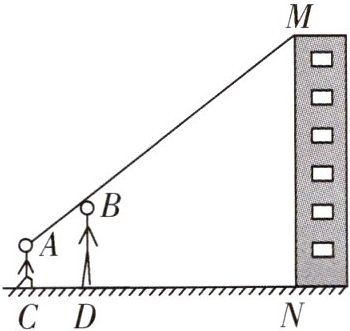
3 一题多解 小亮和小芳准备用测量影子的方法测算住宅楼的高度,但恰逢阴天,于是两人商定改用下面的方法：如图,小亮蹲在地上,小芳站在小亮和楼之间,两人适当调整自己的位置,当楼的顶部M、小芳的头顶B及小亮的眼睛A恰在一条直线上时,两人分别标定自己的位置C,D.然后测出两人之间的距离CD= 1.25m,小芳与楼之间的距离DN= 30m(C,D,N在一条直线上),小芳的身高BD= 1.6m,小亮蹲地观测时眼睛到地面的距离AC= 0.8m.请帮他们求出住宅楼的高度.

答案：
解:解法一 如图1,过点A作AF⊥MN,垂足为点F,交BD于点E,则NF=DE=AC=0.8m,AE=CD=1.25m,EF=DN=30m,∠AEB=∠AFM=90°,
∵∠BAE=∠MAF,
∴△ABE∽△AMF,
∴$\frac{BE}{MF}$=$\frac{AE}{AF}$,即$\frac{1.6−0.8}{MF}$=$\frac{1.25}{1.25+30}$,
∴MF=20m,
∴MN=MF+FN=20+0.8=20.8(m).
答:住宅楼的高度为20.8m.

解法二 如图2,延长MA交直线CN于点G
由AC//BD,易知△GAC∽△GBD,
∴$\frac{GC}{GD}$=$\frac{AC}{BD}$,
即$\frac{GC}{GC+1.25}$=$\frac{0.8}{1.6}$
∴GC=1.25m.
由AC//MN,易知△GAC∽△GMN,
∴$\frac{GC}{GN}$=$\frac{AC}{MN}$,即$\frac{1.25}{1.25+1.25+30}$=$\frac{0.8}{MN}$,
∴MN=20.8m.

答:住宅楼的高度为20.8m.

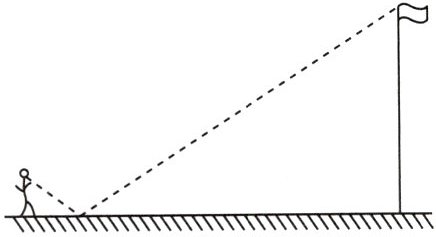
4 [2023南充中考]如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚下水平放置一平面镜,然后向后退(保持脚、镜和旗杆底端在同一直线上),直到她刚好在镜子中看到旗杆的顶端.已知小菲的眼睛离地面高度为1.6m,同时量得小菲与镜子的水平距离为2m,镜子与旗杆的水平距离为10m,则旗杆高度为( )

A.6.4m
B.8m
C.9.6m
D.12.5m

答案：
B 如图,由题意得AB⊥BD,DE⊥BD,
∴∠ABC=∠EDC=90°,
∵∠ACB=∠ECD,
∴△ABC∽△EDC,
∴$\frac{BA}{DE}$=$\frac{BC}{DC}$
∴$\frac{1.6}{DE}$=$\frac{2}{10}$,
∴DE=8m.

归纳总结
利用镜子反射测高的原理
利用物理学中的“入射角等于反射角”的知识可以知道入射光线和反射光线与镜面的夹角相等。由一对锐角对应相等及人与被测物体都与地面垂直，得三角形相似。

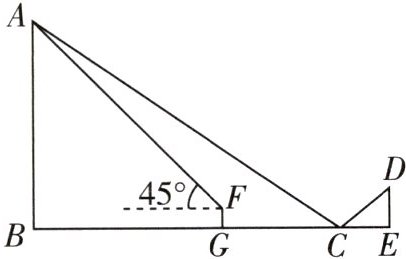
5 [2024成都七中育才学校月考]小高和小张两位同学想利用刚学过的测量知识来测量新建成的科技馆AB的高度.某天,他们带着测量工具来到科技馆前,但由于园区整体规划的原因,他们无法到达科技馆底部B.于是小高在地面上的点C处放置了一个平面镜,如图,小张从C处出发沿着BC方向移动,当移动到点E处时,刚好在平面镜内看到科技馆的顶端A的像,此时,测得CE= 2米,小张眼睛到地面的距离DE为1.6米；然后,小高沿CB方向移动到点G,用测量器测得科技馆顶端A的仰角为45°,此时,测得CG= 8米,测量器的高度FG= 0.8米.已知点B,G,C,E在同一水平直线上,且AB,FG,DE均垂直于BE,求该科技馆的高度AB.

答案：
解:如图,过F作FH⊥AB于点H,则FH=BG,FG=BH=0.8米,△AHF是等腰直角三角形，
∴AH=FH=BG.
根据题意可得∠DCE=∠ACB,
∵∠ABC=∠DEC=90°,
∴△DCE∽△ACB,
∴$\frac{CE}{CB}$=$\frac{DE}{AB}$,
∴$\frac{2}{8+AH}$=$\frac{1.6}{AH+0.8}$,
∴AH=28米,
∴AB=AH+BH=28+0.8=28.8(米).
答:该科技馆的高度AB为28.8米.

8 [2025南阳期中]数学实践小组想利用镜子的反射定律测量池塘边一棵树的高度AB.测量步骤如下：
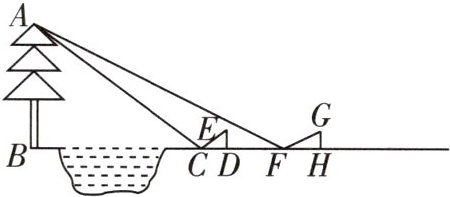
①如图,树与地面垂直,在地面上的点C处放置一块镜子,小明站在BC的延长线上的点D处,当小明在镜子中刚好看到树的顶点A时,测得小明到镜子的水平距离CD= 2米,小明的眼睛E到地面的距离ED= 1.5米；
②将镜子从点C沿BC的延长线向右移动10米到点F处,小明向后移动到BC的延长线上的点H处时,小明的眼睛G又刚好在镜子中看到树的顶点A,这时测得小明到镜子的距离FH= 3米.
请你根据材料中的测量数据,计算树的高度AB.15米

答案： 解:设AB=x米,BC=y米.
∵∠ABC=∠EDC=90°,∠ACB=∠ECD,
∴△ABC∽△EDC,
∴$\frac{AB}{ED}$=$\frac{BC}{DC}$,
∴$\frac{x}{1.5}$=$\frac{y}{2}$,
∵∠ABF=∠GHF=90°,∠AFB=∠GFH,
∴△ABF∽△GHF,
∴$\frac{AB}{GH}$=$\frac{BF}{HF}$,
∴$\frac{x}{1.5}$=$\frac{y + 10}{3}$,
∴$\frac{y}{2}$=$\frac{y + 10}{3}$，解得y=20,
把y=20代入$\frac{x}{1.5}$=$\frac{y}{2}$，得x=15，
∴树的高度AB为15米.