第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
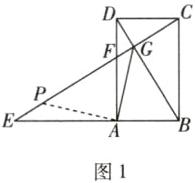
4 一题多解[2024福州期末]如图1,已知四边形ABCD是矩形,点E在BA的延长线上,AE= AD,EC与BD相交于点G,与AD相交于点F,AF= AB.
(1)求证:BD⊥EC.
(2)如图2,连接AG,求证:$EG-DG= \sqrt{2}AG.$

(1)求证:BD⊥EC.
(2)如图2,连接AG,求证:$EG-DG= \sqrt{2}AG.$

答案:
解题思路:
(1)先证明△AEF≌△ADB,得到对应角相等,再通过等量代换即可证明;
(2)以点A为直角顶点、AG为腰构造等腰直角三角形,据此即可证明.
证明:
(1)因为四边形ABCD是矩形,点E在BA的延长线上,所以∠EAF=∠DAB=90°.
又因为AE=AD,AF=AB,
所以△AEF≌△ADB,所以∠AEF=∠ADB,
所以∠GEB+∠GBE=∠ADB+∠ABD=90°,
所以∠EGB=90°,所以BD⊥EC.
(2)解法一 如图1,在线段EG上取点P,使得EP=DG,连接AP.
在△AEP和△ADG中,$\begin{cases}AE=AD,\\∠AEP=∠ADG,\\EP=DG,\end{cases}$
所以△AEP≌△ADG(SAS),所以AP=AG,∠EAP=∠DAG,
所以∠PAG=∠PAD+∠DAG=∠PAD+∠EAP=∠DAE=90°,
所以△PAG为等腰直角三角形.
所以EG−DG=EG−EP=PG=$\sqrt{2}$AG.
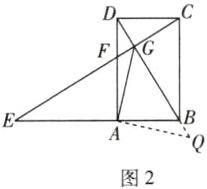
解法二 如图2,过点A作AG的垂线,与DB的延长线交于点Q,连接AQ.
在△AEG和△ADQ中,∠AEG=∠ADQ,AE=AD,∠EAG=90°+∠DAG=∠DAQ,
所以△AEG≌△ADQ,所以EG=DQ,AG=AQ,
所以△AGQ为等腰直角三角形,
所以EG−DG=DQ−DG=QG=$\sqrt{2}$AG.
解题思路:
(1)先证明△AEF≌△ADB,得到对应角相等,再通过等量代换即可证明;
(2)以点A为直角顶点、AG为腰构造等腰直角三角形,据此即可证明.
证明:
(1)因为四边形ABCD是矩形,点E在BA的延长线上,所以∠EAF=∠DAB=90°.
又因为AE=AD,AF=AB,
所以△AEF≌△ADB,所以∠AEF=∠ADB,
所以∠GEB+∠GBE=∠ADB+∠ABD=90°,
所以∠EGB=90°,所以BD⊥EC.
(2)解法一 如图1,在线段EG上取点P,使得EP=DG,连接AP.
在△AEP和△ADG中,$\begin{cases}AE=AD,\\∠AEP=∠ADG,\\EP=DG,\end{cases}$
所以△AEP≌△ADG(SAS),所以AP=AG,∠EAP=∠DAG,
所以∠PAG=∠PAD+∠DAG=∠PAD+∠EAP=∠DAE=90°,
所以△PAG为等腰直角三角形.
所以EG−DG=EG−EP=PG=$\sqrt{2}$AG.


解法二 如图2,过点A作AG的垂线,与DB的延长线交于点Q,连接AQ.
在△AEG和△ADQ中,∠AEG=∠ADQ,AE=AD,∠EAG=90°+∠DAG=∠DAQ,
所以△AEG≌△ADQ,所以EG=DQ,AG=AQ,
所以△AGQ为等腰直角三角形,
所以EG−DG=DQ−DG=QG=$\sqrt{2}$AG.
5 一题多解 如图1,矩形MNPQ中,点E,F,G,H分别在NP,PQ,QM,MN上,若∠1= ∠2= ∠3= ∠4,则称四边形EFGH为矩形MNPQ的反射四边形.图2、图3、图4中,四边形ABCD为矩形,且AB= 4,BC= 8.
理解与作图:
(1)在图2、图3中,点E,F分别在BC,CD边上,试利用正方形网格在图上作出矩形ABCD的反射四边形EFGH.
计算与猜想:
(2)求图2、图3中反射四边形EFGH的周长,并猜想矩形ABCD的反射四边形的周长是否为定值.
启发与证明:
(3)如图4,为了证明上述猜想,小华同学尝试延长GF交BC的延长线于M,试利用小华同学给我们的启发证明(2)中的猜想.

理解与作图:
(1)在图2、图3中,点E,F分别在BC,CD边上,试利用正方形网格在图上作出矩形ABCD的反射四边形EFGH.
计算与猜想:
(2)求图2、图3中反射四边形EFGH的周长,并猜想矩形ABCD的反射四边形的周长是否为定值.
启发与证明:
(3)如图4,为了证明上述猜想,小华同学尝试延长GF交BC的延长线于M,试利用小华同学给我们的启发证明(2)中的猜想.

答案:
解:
(1)作图如下:
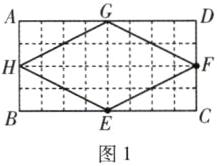

(2)在图1中,EF=FG=GH=HE=$\sqrt{2^{2}+4^{2}}=\sqrt{20}=2\sqrt{5}$,
∴四边形EFGH的周长为8$\sqrt{5}$.
在图2中,EF=GH=$\sqrt{2^{2}+1^{2}}=\sqrt{5}$,FG=HE=$\sqrt{3^{2}+6^{2}}=\sqrt{45}=3\sqrt{5}$,
∴四边形EFGH的周长为2×$\sqrt{5}$+2×3$\sqrt{5}$=8$\sqrt{5}$.
猜想:矩形ABCD的反射四边形的周长为定值.
(3)解法一 如图3,延长GH交CB的延长线于点N.

∵∠1=∠2,∠1=∠5,
∴∠2=∠5,
又
∵FC=FC,∠FCE=∠FCM=90°,
∴Rt△FCE≌Rt△FCM,
∴EF=MF,EC=MC.
同理,NH=EH,NB=EB,
∴MN=2BC=16.
∵∠M=90°−∠5=90°−∠1,∠N=90°−∠3,∠1=∠3,
∴∠M=∠N,
∴GM=GN.
过点G作GK⊥BC于K,则KM=$\frac{1}{2}$MN=8.
∴GM=$\sqrt{GK^{2}+KM^{2}}=\sqrt{4^{2}+8^{2}}=4\sqrt{5}$,
∴四边形EFGH的周长为2GM=8$\sqrt{5}$.
解法二
∵∠1=∠2,∠1=∠5,
∴∠2=∠5.
又
∵FC=FC,∠FCE=∠FCM=90°,
∴Rt△FCE≌Rt△FCM,
∴EF=MF,EC=MC.
∵∠M=90°−∠5=90°−∠1,∠HEB=90°−∠4,
而∠1=∠4,
∴∠M=∠HEB,
∴HE//GF.
同理,GH//EF,
∴四边形EFGH是平行四边形,
∴FG=HE,
而∠1=∠4,∠FDG=∠HBE=90°,
∴Rt△FDG≌Rt△HBE,
∴DG=BE.
过点G作GK⊥BC于点K,则KM=KC+CM=DG+CM=BE+EC=8,
∴GM=$\sqrt{GK^{2}+KM^{2}}=\sqrt{4^{2}+8^{2}}=4\sqrt{5}$,
∴四边形EFGH的周长为2GM=8$\sqrt{5}$.
解:
(1)作图如下:


(2)在图1中,EF=FG=GH=HE=$\sqrt{2^{2}+4^{2}}=\sqrt{20}=2\sqrt{5}$,
∴四边形EFGH的周长为8$\sqrt{5}$.
在图2中,EF=GH=$\sqrt{2^{2}+1^{2}}=\sqrt{5}$,FG=HE=$\sqrt{3^{2}+6^{2}}=\sqrt{45}=3\sqrt{5}$,
∴四边形EFGH的周长为2×$\sqrt{5}$+2×3$\sqrt{5}$=8$\sqrt{5}$.
猜想:矩形ABCD的反射四边形的周长为定值.
(3)解法一 如图3,延长GH交CB的延长线于点N.

∵∠1=∠2,∠1=∠5,
∴∠2=∠5,
又
∵FC=FC,∠FCE=∠FCM=90°,
∴Rt△FCE≌Rt△FCM,
∴EF=MF,EC=MC.
同理,NH=EH,NB=EB,
∴MN=2BC=16.
∵∠M=90°−∠5=90°−∠1,∠N=90°−∠3,∠1=∠3,
∴∠M=∠N,
∴GM=GN.
过点G作GK⊥BC于K,则KM=$\frac{1}{2}$MN=8.
∴GM=$\sqrt{GK^{2}+KM^{2}}=\sqrt{4^{2}+8^{2}}=4\sqrt{5}$,
∴四边形EFGH的周长为2GM=8$\sqrt{5}$.
解法二
∵∠1=∠2,∠1=∠5,
∴∠2=∠5.
又
∵FC=FC,∠FCE=∠FCM=90°,
∴Rt△FCE≌Rt△FCM,
∴EF=MF,EC=MC.
∵∠M=90°−∠5=90°−∠1,∠HEB=90°−∠4,
而∠1=∠4,
∴∠M=∠HEB,
∴HE//GF.
同理,GH//EF,
∴四边形EFGH是平行四边形,
∴FG=HE,
而∠1=∠4,∠FDG=∠HBE=90°,
∴Rt△FDG≌Rt△HBE,
∴DG=BE.
过点G作GK⊥BC于点K,则KM=KC+CM=DG+CM=BE+EC=8,
∴GM=$\sqrt{GK^{2}+KM^{2}}=\sqrt{4^{2}+8^{2}}=4\sqrt{5}$,
∴四边形EFGH的周长为2GM=8$\sqrt{5}$.
查看更多完整答案,请扫码查看


