第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
9 [2024临夏州中考]如图,O是坐标原点,菱形ABOC的顶点B在x轴的负半轴上,顶点C的坐标为(3,4),则顶点A的坐标为 ( )
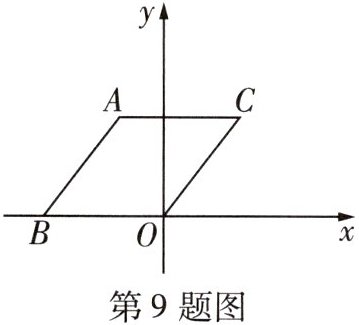
A. $ (-4,2) $
B. $ (-\sqrt{3},4) $
C. $ (-2,4) $
D. $ (-4,\sqrt{3}) $

A. $ (-4,2) $
B. $ (-\sqrt{3},4) $
C. $ (-2,4) $
D. $ (-4,\sqrt{3}) $
答案:
C 如图,过点 C 作 $ CN \perp x $ 轴于 N,过点 A 作 $ AM \perp x $ 轴于点 M,
∵ 点 C 的坐标为 $ ( 3,4 ) $,
∴ $ ON = 3 $,$ CN = 4 $,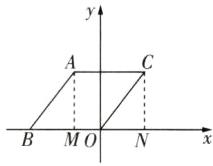
∴ $ OC = \sqrt{ON^{2} + CN^{2}} = \sqrt{3^{2} + 4^{2}} = 5 $。
∵ 四边形 ABOC 是菱形,
∴ $ AC = OC = 5 $,$ AC // BO $,
∴ 点 A 的坐标为 $ ( - 2,4 ) $。
C 如图,过点 C 作 $ CN \perp x $ 轴于 N,过点 A 作 $ AM \perp x $ 轴于点 M,
∵ 点 C 的坐标为 $ ( 3,4 ) $,
∴ $ ON = 3 $,$ CN = 4 $,

∴ $ OC = \sqrt{ON^{2} + CN^{2}} = \sqrt{3^{2} + 4^{2}} = 5 $。
∵ 四边形 ABOC 是菱形,
∴ $ AC = OC = 5 $,$ AC // BO $,
∴ 点 A 的坐标为 $ ( - 2,4 ) $。
10 [2024德州月考]如图,菱形ABCD的对角线AC,BD交于点O,$ AC = 4 $,$ BD = 16 $,将$ △ABO $沿AC方向平移,得到$ △A'B'O' $. 当点A的对应点$ A' $与点C重合时,点A与点$ B' $之间的距离为 (
A. 6
B. 8
C. 10
D. 12
C
)A. 6
B. 8
C. 10
D. 12
答案:
C 由菱形的性质可知 $ OB = 8 $,$ OA = 2 $,$ AC \perp BD $。由平移的性质,得 $ O'B' = OB = 8 $,$ O'A = 3OA = 6 $,$ \angle AO'B' = \angle AOB = 90^{\circ} $,
∴ $ AB' = \sqrt{O'B'^{2} + O'A^{2}} = \sqrt{8^{2} + 6^{2}} = 10 $。
∴ $ AB' = \sqrt{O'B'^{2} + O'A^{2}} = \sqrt{8^{2} + 6^{2}} = 10 $。
11 一题多解[2025汕头五校联考]如图,AC为菱形ABCD的对角线,$ ∠ACD = 30^{\circ} $,过点D作$ DE ⊥ BC $,垂足为点E,则$ \frac{CE}{AD} = $ (
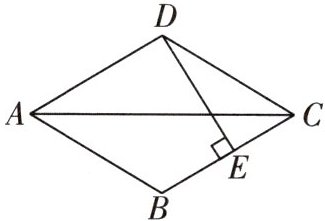
A. $ \frac{1}{3} $
B. $ \frac{1}{2} $
C. $ \frac{\sqrt{3}}{3} $
D. $ \frac{\sqrt{3}}{2} $
B
)
A. $ \frac{1}{3} $
B. $ \frac{1}{2} $
C. $ \frac{\sqrt{3}}{3} $
D. $ \frac{\sqrt{3}}{2} $
答案:
B
解法一:因为四边形 ABCD 是菱形,所以 $ CD = AD $,AC 平分 $ \angle BCD $。因为 $ \angle ACD = 30^{\circ} $,所以 $ \angle BCD = 2 \angle ACD = 60^{\circ} $。因为 $ DE \perp BC $,所以 $ \angle DEC = 90^{\circ} $,所以在 $ \mathrm{Rt} \triangle CDE $ 中,$ \angle CDE = 30^{\circ} $,所以 $ CE = \frac{1}{2}CD = \frac{1}{2}AD $,即 $ \frac{CE}{AD} = \frac{1}{2} $。
解法二:连接 BD,易证 $ \triangle BCD $ 是等边三角形。因为 $ DE \perp BC $,所以 $ BE = CE = \frac{1}{2}BD = \frac{1}{2}AD $,即 $ \frac{CE}{AD} = \frac{1}{2} $。
解法一:因为四边形 ABCD 是菱形,所以 $ CD = AD $,AC 平分 $ \angle BCD $。因为 $ \angle ACD = 30^{\circ} $,所以 $ \angle BCD = 2 \angle ACD = 60^{\circ} $。因为 $ DE \perp BC $,所以 $ \angle DEC = 90^{\circ} $,所以在 $ \mathrm{Rt} \triangle CDE $ 中,$ \angle CDE = 30^{\circ} $,所以 $ CE = \frac{1}{2}CD = \frac{1}{2}AD $,即 $ \frac{CE}{AD} = \frac{1}{2} $。
解法二:连接 BD,易证 $ \triangle BCD $ 是等边三角形。因为 $ DE \perp BC $,所以 $ BE = CE = \frac{1}{2}BD = \frac{1}{2}AD $,即 $ \frac{CE}{AD} = \frac{1}{2} $。
12 [2024成都浦江中学期中]如图,在菱形ABCD中,AC与BD相交于点O,AB的垂直平分线EF交AC于点F,交AB于点E,连接DF. 若$ ∠BAD = 80^{\circ} $,则$ ∠CDF $的度数为______.


答案:
$ 60^{\circ} $ 如图,连接 BF,
∵ 四边形 ABCD 是菱形,$ \angle BAD = 80^{\circ} $,
∴ $ \angle DAC = 40^{\circ} $,$ \angle ADC = 100^{\circ} $,$ AC \perp BD $,$ DO = BO $,
∴ $ BF = DF $。
∵ EF 垂直平分 AB,
∴ $ AF = BF $,
∴ $ AF = DF $,
∴ $ \angle ADF = \angle FAD = 40^{\circ} $,
∴ $ \angle CDF = 60^{\circ} $。

归纳总结
菱形的性质在解题中的应用
(1)菱形的每一条对角线均平分一组对角,可以用来证明角相等;(2)菱形的对角线互相垂直,可以用来证明线段垂直;(3)一个内角是 $ 60^{\circ} $ 的菱形,较短的对角线将其分成两个全等的等边三角形;(4)两条对角线将菱形分为四个全等的直角三角形。这是解决与菱形有关的问题时常用到的结论。
$ 60^{\circ} $ 如图,连接 BF,
∵ 四边形 ABCD 是菱形,$ \angle BAD = 80^{\circ} $,
∴ $ \angle DAC = 40^{\circ} $,$ \angle ADC = 100^{\circ} $,$ AC \perp BD $,$ DO = BO $,
∴ $ BF = DF $。
∵ EF 垂直平分 AB,
∴ $ AF = BF $,
∴ $ AF = DF $,
∴ $ \angle ADF = \angle FAD = 40^{\circ} $,
∴ $ \angle CDF = 60^{\circ} $。

归纳总结
菱形的性质在解题中的应用
(1)菱形的每一条对角线均平分一组对角,可以用来证明角相等;(2)菱形的对角线互相垂直,可以用来证明线段垂直;(3)一个内角是 $ 60^{\circ} $ 的菱形,较短的对角线将其分成两个全等的等边三角形;(4)两条对角线将菱形分为四个全等的直角三角形。这是解决与菱形有关的问题时常用到的结论。
13 [2024石嘴山八中期中]如图,在菱形ABCD中,$ AB = 2 $,$ ∠ABC = 120^{\circ} $,E是AB的中点,P是对角线AC上的一个动点,则$ PE + PB $的最小值是______.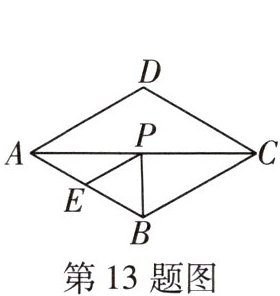

答案:
$ \sqrt{3} $ 有关直线同侧的折线段长度和最小问题,常转化为直线两侧两点之间线段最短问题,即将点 B 借助菱形的对称性转移到点 D。如图,连接 DE 交 AC 于点 P,易知 $ PB = PD $,此时 $ PE + PB $ 最小,最小值为 DE 的长。因为四边形 ABCD 是菱形,所以 $ AD = AB = 2 $。因为 E 是 AB 的中点,所以 $ AE = \frac{1}{2}AB = 1 $。易知 DE 垂直平分 AB,在 $ \mathrm{Rt} \triangle ADE $ 中,$ DE = \sqrt{AD^{2} - AE^{2}} = \sqrt{3} $,即 $ PE + PB $ 的最小值为 $ \sqrt{3} $。

$ \sqrt{3} $ 有关直线同侧的折线段长度和最小问题,常转化为直线两侧两点之间线段最短问题,即将点 B 借助菱形的对称性转移到点 D。如图,连接 DE 交 AC 于点 P,易知 $ PB = PD $,此时 $ PE + PB $ 最小,最小值为 DE 的长。因为四边形 ABCD 是菱形,所以 $ AD = AB = 2 $。因为 E 是 AB 的中点,所以 $ AE = \frac{1}{2}AB = 1 $。易知 DE 垂直平分 AB,在 $ \mathrm{Rt} \triangle ADE $ 中,$ DE = \sqrt{AD^{2} - AE^{2}} = \sqrt{3} $,即 $ PE + PB $ 的最小值为 $ \sqrt{3} $。

14 推理能力[2024九江十一中月考]在菱形ABCD中,$ ∠ABC = 60^{\circ} $,E是对角线AC上一点,F是线段BC的延长线上一点,且$ CF = AE $,连接BE,EF. 如图1,当点E是线段AC的中点时,易证$ BE = EF $.
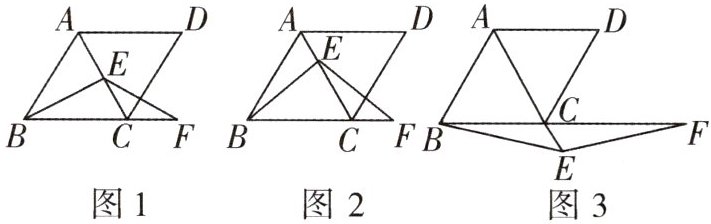
(1)如图2,当点E不是线段AC的中点,其他条件不变时,请你判断结论:$ BE = EF $______
(2)如图3,当点E是线段AC的延长线上一点,其他条件不变时,结论$ BE = EF $是否成立? 若成立,请给予证明;若不成立,请说明理由.

(1)如图2,当点E不是线段AC的中点,其他条件不变时,请你判断结论:$ BE = EF $______
成立
.(填“成立”或“不成立”)(2)如图3,当点E是线段AC的延长线上一点,其他条件不变时,结论$ BE = EF $是否成立? 若成立,请给予证明;若不成立,请说明理由.
答案:
解:(1)成立
过点 E 作 $ EG // BC $ 交 AB 于点 G。
∵ 四边形 ABCD 为菱形,
∴ $ AB = BC $。
又
∵ $ \angle ABC = 60^{\circ} $,
∴ $ \triangle ABC $ 是等边三角形。
∴ $ AB = AC $,$ \angle BAC = \angle ACB = 60^{\circ} $。
∵ $ EG // BC $,
∴ $ \angle AGE = \angle ABC = 60^{\circ} $。
又
∵ $ \angle BAC = 60^{\circ} $,
∴ $ \triangle AGE $ 是等边三角形。
∴ $ AG = AE = GE $,
∴ $ BG = EC $。
∵ $ CF = AE $,
∴ $ GE = CF $。
∵ $ \angle AGE = \angle ACB = 60^{\circ} $,
∴ $ \angle BGE = \angle ECF = 120^{\circ} $。
∴ $ \triangle BGE \cong \triangle ECF $,
∴ $ BE = EF $。
(2)结论 $ BE = EF $ 成立。证明如下:
过点 E 作 $ EQ // BC $ 交 AB 的延长线于点 Q。
∵ 四边形 ABCD 为菱形,
∴ $ AB = BC $。
又
∵ $ \angle ABC = 60^{\circ} $,
∴ $ \triangle ABC $ 是等边三角形。
∴ $ AB = AC $,$ \angle BAC = \angle ACB = 60^{\circ} $。
∵ $ EQ // BC $,
∴ $ \angle AQE = \angle ABC = 60^{\circ} $。
又
∵ $ \angle BAC = 60^{\circ} $,
∴ $ \triangle AQE $ 是等边三角形。
∴ $ AQ = AE = QE $,
∴ $ BQ = EC $。
∵ $ CF = AE $,
∴ $ QE = CF $。
又
∵ $ \angle ECF = \angle ACB = 60^{\circ} $,
∴ $ \angle BQE = \angle ECF $。
∴ $ \triangle BQE \cong \triangle ECF $,
∴ $ BE = EF $。
过点 E 作 $ EG // BC $ 交 AB 于点 G。
∵ 四边形 ABCD 为菱形,
∴ $ AB = BC $。
又
∵ $ \angle ABC = 60^{\circ} $,
∴ $ \triangle ABC $ 是等边三角形。
∴ $ AB = AC $,$ \angle BAC = \angle ACB = 60^{\circ} $。
∵ $ EG // BC $,
∴ $ \angle AGE = \angle ABC = 60^{\circ} $。
又
∵ $ \angle BAC = 60^{\circ} $,
∴ $ \triangle AGE $ 是等边三角形。
∴ $ AG = AE = GE $,
∴ $ BG = EC $。
∵ $ CF = AE $,
∴ $ GE = CF $。
∵ $ \angle AGE = \angle ACB = 60^{\circ} $,
∴ $ \angle BGE = \angle ECF = 120^{\circ} $。
∴ $ \triangle BGE \cong \triangle ECF $,
∴ $ BE = EF $。
(2)结论 $ BE = EF $ 成立。证明如下:
过点 E 作 $ EQ // BC $ 交 AB 的延长线于点 Q。
∵ 四边形 ABCD 为菱形,
∴ $ AB = BC $。
又
∵ $ \angle ABC = 60^{\circ} $,
∴ $ \triangle ABC $ 是等边三角形。
∴ $ AB = AC $,$ \angle BAC = \angle ACB = 60^{\circ} $。
∵ $ EQ // BC $,
∴ $ \angle AQE = \angle ABC = 60^{\circ} $。
又
∵ $ \angle BAC = 60^{\circ} $,
∴ $ \triangle AQE $ 是等边三角形。
∴ $ AQ = AE = QE $,
∴ $ BQ = EC $。
∵ $ CF = AE $,
∴ $ QE = CF $。
又
∵ $ \angle ECF = \angle ACB = 60^{\circ} $,
∴ $ \angle BQE = \angle ECF $。
∴ $ \triangle BQE \cong \triangle ECF $,
∴ $ BE = EF $。
查看更多完整答案,请扫码查看


