第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
1 [2024大连中山区期末]如图,$l_{1}// l_{2}// l_{3}$,直线AC,DF与这三条平行线分别交于点A,B,C和点D,E,F,若$AB= 4$,$DE= 3$,$EF= 6$,则BC的长是(
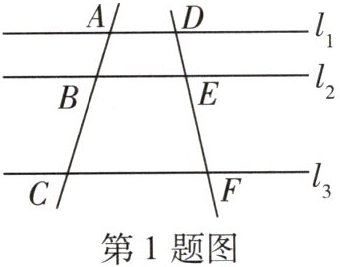
A. 4
B. 6
C. 8
D. 12
8
)
A. 4
B. 6
C. 8
D. 12
答案:
C
∵l₁//l₂//l₃,
∴$\frac{AB}{BC}$=$\frac{DE}{EF}$,
∴$\frac{4}{BC}$=$\frac{3}{6}$,
∴BC = 8.
∵l₁//l₂//l₃,
∴$\frac{AB}{BC}$=$\frac{DE}{EF}$,
∴$\frac{4}{BC}$=$\frac{3}{6}$,
∴BC = 8.
安溪雁塔,位于安溪县城凤城镇的东南面,是县级文物保护单位.如图是安溪雁塔及其部分示意图,已知$AD// BE// CF$,若$\frac {AB}{BC}= \frac {1}{2}$,则$\frac {EF}{DF}$的值为(
A. $\frac {1}{3}$
B. $\frac {1}{2}$
C. $\frac {2}{3}$
D. $\frac {3}{4}$
$\frac{2}{3}$
)A. $\frac {1}{3}$
B. $\frac {1}{2}$
C. $\frac {2}{3}$
D. $\frac {3}{4}$
答案:
变式 C
∵AD//BE//CF,
∴$\frac{DE}{EF}$=$\frac{AB}{BC}$=$\frac{1}{2}$,
∴EF = 2DE,
∴DF = 3DE,
∴$\frac{EF}{DF}$=$\frac{2DE}{3DE}$=$\frac{2}{3}$.
∵AD//BE//CF,
∴$\frac{DE}{EF}$=$\frac{AB}{BC}$=$\frac{1}{2}$,
∴EF = 2DE,
∴DF = 3DE,
∴$\frac{EF}{DF}$=$\frac{2DE}{3DE}$=$\frac{2}{3}$.
2 教材P84T1变式[2023北京中考]如图,直线AD,BC交于点O,$AB// EF// CD$,若$AO= 2$,$OF= 1$,$FD= 2$,则$\frac {BE}{EC}$的值为
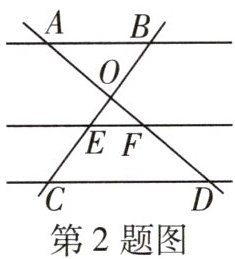
$\frac{3}{2}$
.
答案:
2 $\frac{3}{2}$
∵AO = 2,OF = 1,
∴AF = AO + OF = 2 + 1 = 3,
∵AB//EF//CD,
∴$\frac{BE}{EC}$=$\frac{AF}{FD}$=$\frac{3}{2}$.
∵AO = 2,OF = 1,
∴AF = AO + OF = 2 + 1 = 3,
∵AB//EF//CD,
∴$\frac{BE}{EC}$=$\frac{AF}{FD}$=$\frac{3}{2}$.
3 [2024上海松江区一模]如图,已知直线$l_{1}$,$l_{2}$,$l_{3}$分别交直线m于点A,B,C,交直线n于点D,E,F,且$l_{1}// l_{2}// l_{3}$,$AB= 2BC$,$DF= 6$,那么$EF= $
2
.
答案:
3 2
∵l₁//l₂//l₃,AB = 2BC,
∴$\frac{AB}{BC}$=$\frac{DE}{EF}$ = 2,
∵DE = DF - EF = 6 - EF,
∴$\frac{6 - EF}{EF}$ = 2, 解得 EF = 2.
∵l₁//l₂//l₃,AB = 2BC,
∴$\frac{AB}{BC}$=$\frac{DE}{EF}$ = 2,
∵DE = DF - EF = 6 - EF,
∴$\frac{6 - EF}{EF}$ = 2, 解得 EF = 2.
4 [2025长春108中月考]如图是一架梯子的示意图,其中$AA_{1}// BB_{1}// CC_{1}// DD_{1}$,且$AB= BC= CD$.为使其更稳固,在A,$D_{1}$间加绑一条安全绳(线段$AD_{1}$),$AD_{1}交BB_{1}$于点E,量得$AE= 0.4m$,则$AD_{1}= $
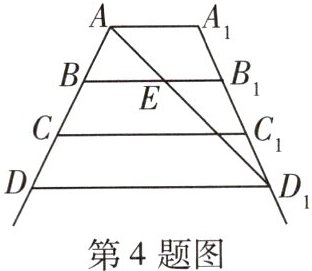
1.2
m.
答案:
4 1.2
∵AA₁//BB₁//CC₁//DD₁, 且 AB = BC = CD,
∴$\frac{AE}{AD₁}$=$\frac{AB}{AD}$=$\frac{1}{3}$, 又
∵AE = 0.4m,
∴AD₁ = 3AE = 1.2m.
∵AA₁//BB₁//CC₁//DD₁, 且 AB = BC = CD,
∴$\frac{AE}{AD₁}$=$\frac{AB}{AD}$=$\frac{1}{3}$, 又
∵AE = 0.4m,
∴AD₁ = 3AE = 1.2m.
5 [2023吉林中考]如图,在$\triangle ABC$中,点D在边AB上,过点D作$DE// BC$,交AC于点E.若$AD= 2$,$BD= 3$,则$\frac {AE}{AC}$的值是(
A. $\frac {2}{5}$
B. $\frac {1}{2}$
C. $\frac {3}{5}$
D. $\frac {2}{3}$
$\frac{2}{5}$
)A. $\frac {2}{5}$
B. $\frac {1}{2}$
C. $\frac {3}{5}$
D. $\frac {2}{3}$
答案:
5 A
∵DE//BC,
∴$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{AD}{AD + BD}$=$\frac{2}{2 + 3}$=$\frac{2}{5}$.
∵DE//BC,
∴$\frac{AE}{AC}$=$\frac{AD}{AB}$=$\frac{AD}{AD + BD}$=$\frac{2}{2 + 3}$=$\frac{2}{5}$.
如图,在$\triangle ABC$中,$DE// AB$,若$\frac {CD}{CA}= \frac {3}{5}$,$CE= 9$,则BE的长为(
A. 6
B. 9
C. 12
D. 15
6
)A. 6
B. 9
C. 12
D. 15
答案:
变式 A
∵DE//AB,$\frac{CD}{CA}$=$\frac{3}{5}$,
∴$\frac{CE}{CB}$=$\frac{CD}{CA}$=$\frac{3}{5}$.
∵CE = 9,
∴$\frac{9}{CB}$=$\frac{3}{5}$,
∴CB = 15,
∴BE = CB - CE = 15 - 9 = 6.
∵DE//AB,$\frac{CD}{CA}$=$\frac{3}{5}$,
∴$\frac{CE}{CB}$=$\frac{CD}{CA}$=$\frac{3}{5}$.
∵CE = 9,
∴$\frac{9}{CB}$=$\frac{3}{5}$,
∴CB = 15,
∴BE = CB - CE = 15 - 9 = 6.
如图,$DE// BC$,$DF// AC$,$AD= 4cm$,$AB= 12cm$,$DE= 5cm$,则线段BF的长为
10
cm.
答案:
6 10
∵DE//BC,DF//AC,
∴四边形DFCE为平行四边形,
∴FC = DE = 5cm.
∵DF//AC,
∴$\frac{AD}{AB}$=$\frac{FC}{CB}$, 即 $\frac{4}{12}$=$\frac{5}{CB}$, 解得CB = 15cm,
∴BF = CB - FC = 15 - 5 = 10(cm).
∵DE//BC,DF//AC,
∴四边形DFCE为平行四边形,
∴FC = DE = 5cm.
∵DF//AC,
∴$\frac{AD}{AB}$=$\frac{FC}{CB}$, 即 $\frac{4}{12}$=$\frac{5}{CB}$, 解得CB = 15cm,
∴BF = CB - FC = 15 - 5 = 10(cm).
7 教材P85T3变式如图,在$\triangle ABC$中,D为AC上一点,E为CB延长线上的一点,连接ED交AB于点F,且$\frac {AC}{BC}= \frac {EF}{FD}$,$DG// AB$.求证:$AD= EB$.
证明: ∵DG//AB,∴
证明: ∵DG//AB,∴
$\frac{AC}{AD}=\frac{BC}{BG}$
,$\frac{EF}{FD}=\frac{EB}{BG}$
,∴$\frac{AC}{BC}=\frac{AD}{BG}$.∵$\frac{AC}{BC}=\frac{EF}{FD}$,∴$\frac{AD}{BG}=\frac{EB}{BG}$
,∴AD = EB.
答案:
7 证明:
∵DG//AB,
∴$\frac{AC}{AD}$=$\frac{BC}{BG}$,$\frac{EF}{FD}$=$\frac{EB}{BG}$,
∴$\frac{AC}{BC}$=$\frac{AD}{BG}$.
∵$\frac{AC}{BC}$=$\frac{EF}{FD}$,
∴$\frac{AD}{BG}$=$\frac{EB}{BG}$,
∴AD = EB.
∵DG//AB,
∴$\frac{AC}{AD}$=$\frac{BC}{BG}$,$\frac{EF}{FD}$=$\frac{EB}{BG}$,
∴$\frac{AC}{BC}$=$\frac{AD}{BG}$.
∵$\frac{AC}{BC}$=$\frac{EF}{FD}$,
∴$\frac{AD}{BG}$=$\frac{EB}{BG}$,
∴AD = EB.
查看更多完整答案,请扫码查看


