《2025年同步精练广东人民出版社七年级数学下册北师大版》

3. 如图所示，一个游戏转盘中，红、黄、蓝三个扇形的圆心角度数分别为60°，90°，210°。让转盘自由转动，停止后指针落在红色区域的概率是________。

答案： $\frac{1}{6}$

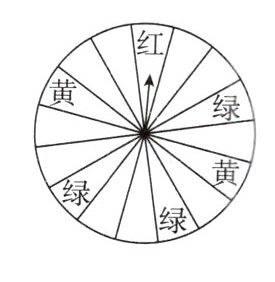
4. 某商场为了吸引顾客，设立了一个可以自由转动的转盘，如图所示，并规定顾客每购买200元商品，就能获得一次转动转盘的机会，若转盘停止后，指针对准红、黄、绿的区域，顾客就可以分别获得50元、20元、10元的奖金，对准无色区域则无奖金（转盘被等分成16份）。
（1）小明购物180元，他获得奖金的概率是多少？
（2）小德购物210元，他获得奖金的概率是多少？
（3）现商场想将获得10元奖金的概率调整为$\frac{1}{4}$，其他金额的获奖率不变，则需要将多少个无色区域涂上绿色？

答案： 解：
(1) 因为180＜200，所以小明购物180元，不能获得转动转盘的机会。所以小明获得奖金的概率为0。
(2) 小德购物210元，能获得一次转动转盘的机会，获得奖金的概率是$\frac{6}{16}=\frac{3}{8}$。
(3) 设需要将x个无色区域涂上绿色，则有$\frac{x + 3}{16}=\frac{1}{4}$，解得x = 1，所以需要将1个无色区域涂上绿色。

1.（2023连云港）如图所示是由16个相同的小正方形和4个相同的大正方形组成的图形，在这个图形内任取一点P，则点P落在阴影部分的概率为 （ ）

A. $\frac{5}{8}$
B. $\frac{13}{50}$
C. $\frac{13}{32}$
D. $\frac{5}{16}$

答案： B

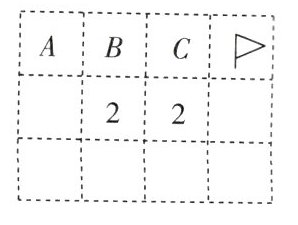
2. 如图所示是扫雷游戏的一部分（说明：图中数字2表示在以该数字为中心相邻的8个方格中有2个地雷）。小旗表示该方格已被探明有地雷，现在还剩下A，B，C三个方格未被探明，其他地方为安全区（包括有数字的方格）。
（1）现在还剩下几个地雷？
（2）A，B，C三个方格中有地雷的概率分别是多大？

答案： 解：由B下面的数字2，可知未被探明的A，B，C中必有2个地雷；由C下面的数字2，以及C右边已探明一个地雷，可知B，C中必有1个地雷；因此，A必有地雷，B或C中有一个地雷。
(1) 现在还剩2个地雷。
(2) $P(A有地雷)=1$，$P(B有地雷)=\frac{1}{2}$，$P(C有地雷)=\frac{1}{2}$。