《2025年同步精练广东人民出版社七年级数学下册北师大版》

1. 三角形全等的判定方法包括（ ）
①SSS；②SAS；③AAA；④AAS；⑤ASA。
A. ①②③④
B. ①③④⑤
C. ①②④⑤
D. ②③④⑤

答案： C

2. 如图所示，要使△AOB≌△AOC，在∠1 = ∠2 的情况下，还需添加一个条件是______（填一个即可）。

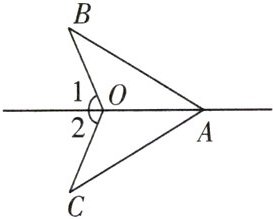
答案： OB = OC（答案不唯一）

3. 某校数学小组为测量校内攀岩墙 AM 的高度，设计了如下方案：如图所示，首先找一根长度大于 AM 的直杆，使直杆斜靠在墙上，且顶端与点 A 重合，记录直杆与地面的夹角∠ABM = 55°，然后使直杆顶端沿墙面竖直缓慢下滑，直到∠MDC = 35°，标记此时直杆的底端点 D，最后测得 DM = 7 m，则攀岩墙的高度 AM = ______ m。

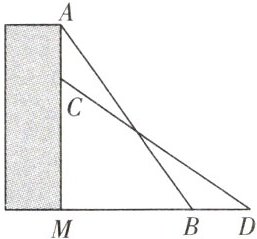
答案： 7

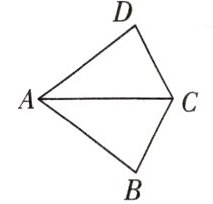
例1 如图所示，在△ABC 与△ADC 中，已知 AD = AB。
（1）在不添加任何辅助线的前提下，以下条件中，能使△ABC≌△ADC 的条件有______（填序号）。
①DC = BC；②∠D = ∠B；③∠DAC = ∠BAC；④∠DCA = ∠BCA。
（2）分别在（1）中添加条件的情况下说明△ABC≌△ADC，并指出两个三角形全等的判定依据。

答案： 解：（1）①③ （2）当添加①DC = BC， 在△ABC和△ADC中， 因为AB = AD，AC = AC，BC = DC， 所以△ABC≌△ADC（SSS）。 当添加③∠DAC = ∠BAC时， 在△ABC和△ADC中， 因为AB = AD，∠BAC = ∠DAC，AC = AC， 所以△ABC≌△ADC（SAS）。

1. （2024 九江期末）如图所示，∠ABC = ∠BAD，请你添加一个条件：____________，使△ABC≌△BAD（只添一个即可）。

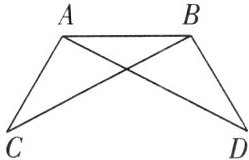
答案： BC = AD（答案不唯一）

2. 如图所示，四边形 ABCD 中，AD//BC，点 E 在对角线 BD 上，且 BE = DA，如果______，那么△ADB≌△EBC。请填上能使结论成立的一个条件，并说明理由。

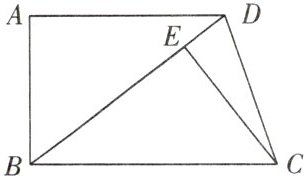
答案： 解：（答案不唯一）添加条件：BD = BC。 理由如下：因为AD//BC， 所以∠ADB = ∠CBE。 在△ADB和△EBC中， $\begin{cases}AD = BE,\\\angle ADB = \angle CBE,\\BD = BC,\end{cases}$ 所以△ADB≌△EBC（SAS）。