《2025年同步精练广东人民出版社七年级数学下册北师大版》

例1 如图所示，$AC// DF$，$AB// EF$，点$D$，$E$分别在$AB$，$AC$上。若$\angle2 = 50^{\circ}$，求$\angle1$的度数。

答案： 解：因为AB//EF，所以∠A = ∠2 = 50°。因为AC//DF，所以∠1 = ∠A = 50°。

例2 如图所示，某科学兴趣小组发现，将光线$AB$照在平面镜$MN$上会形成反射光线$BP$，且两条光线与$MN$形成的夹角相等，即$\angle MBA=\angle NBP$。将一条平行于$AB$的光线$CD$照在平面镜$EF$上，两条反射光线交于点$P$，若$\angle CDP = 40^{\circ}$，$\angle BPD = 70^{\circ}$，求$AB$与$MN$形成的夹角（锐角）的度数。

答案： 解：如图所示，过点P作PQ//AB，则PQ//CD。因为∠CDP = 40°，所以∠DPQ = ∠CDP = 40°。因为∠BPD = 70°，所以∠BPQ = 30°，所以∠ABP = ∠BPQ = 30°。因为∠MBA = ∠NBP，所以∠MBA = $\frac{1}{2}$(180° - ∠ABP) = 75°，即AB与MN形成的夹角（锐角）的度数为75°。

3. 如图所示的是一个探照灯灯碗的纵剖面，从位于$O$点的灯泡发出的两束光线$OB$，$OC$经灯碗反射后平行射出。若$\angle ABO = 30^{\circ}$，$\angle DCO = 80^{\circ}$，则$\angle BOC$的度数为_____。

答案： 110°

4. 如图所示，已知直线$AB// CD$，直线$EF$分别交直线$AB$，$CD$于点$E$，$F$，点$G$为$AB$上一点，连接$FG$，$FG$平分$\angle EFD$，$\angle EGF = 35^{\circ}$，求$\angle1$的度数。

答案： 解：因为AB//CD，∠EGF = 35°，所以∠EGF = ∠GFD = 35°。因为FG平分∠EFD交AB于点G，所以∠EFD = 2∠GFD = 2×35° = 70°。因为AB//CD，所以∠1 = ∠EFD = 70°。

例3 如图所示，已知$a// b$，若$AB$与$BC$的夹角为$105^{\circ}$，$\angle1 = 55^{\circ}$，求$\angle2$的度数。

答案： 解：如图所示，过点B作BD//a，因为a//b，所以a//BD//b，所以∠1 = ∠ABD = 55°，∠2 + ∠CBD = 180°。又因为AB与BC的夹角为105°，即∠ABC = 105°，所以∠CBD = 105° - 55° = 50°，所以∠2 = 180° - 50° = 130°。

5. 如图所示，$AB// CD$，$AE// CF$，若$\angle A = 40^{\circ}$，则$\angle C$的度数为________。

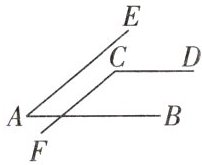
答案： 140°

6. 如图所示，在直角三角形$ABC$中，$\angle C = 90^{\circ}$，$DE\perp AC$交$AC$于点$E$，交$AB$于点$D$。
（1）请分别写出当$BC$，$DE$被$AB$所截时，$\angle B$的同位角、内错角和同旁内角。
（2）试说明$\angle1=\angle2=\angle B$。

答案： 解：（1）当BC，DE被AB所截时，∠B的同位角为∠1；∠B的内错角为∠2；∠B的同旁内角为∠BDE。（2）因为∠C = 90°，DE⊥AC，所以∠AED = ∠C，所以DE//BC，所以∠1 = ∠B。因为∠1 = ∠2，所以∠1 = ∠2 = ∠B。

1.（2024聊城期末）如图所示，$a// b$，$\angle1 = 140^{\circ}$，$\angle2 = 105^{\circ}$，则$\angle3$的度数是________。

答案： 65°

2.（2024济宁期中）如图所示的是某电动伸缩遮阳帘的形状示意图。已知$AF// CD$，小明观察分析该图形得出图中$\angle A$，$\angle ABC$，$\angle C$之间存在如下数量关系：$\angle ABC=\angle A+\angle C$。他的证明思路如下，请将他的证明过程补充完整。

证明：如图所示，过点$B$作直线$BM$，使$BM// AF$。
因为$BM// AF$，$AF// CD$，
所以$BM// CD$(________________)。
因为$BM// AF$，
所以$\angle A=\angle ABM$(________________)。
因为__________，
所以$\angle MBC=\angle C$(________________)。
因为$\angle ABC=\angle ABM+\angle MBC$，
所以$\angle ABC=$________（等量代换）。

答案： 平行于同一条直线的两条直线平行@@两直线平行，内错角相等@@BM//CD@@两直线平行，内错角相等@@∠A + ∠C