《2025年同步精练广东人民出版社七年级数学下册北师大版》

例1 计算：
- （1）$(-4x)(2x^{2}+3x - 1)$；
- （2）$(\frac{2}{3}ab^{2}-2ab)\cdot\frac{1}{2}ab$；
- （3）$(3x^{2}y - xy^{2})\cdot3xy$；
- （4）$(-3x^{2})\cdot(4x^{2}-\frac{4}{9}x + 1)$。

答案： 解：
(1) 原式$ = -8x^{3}-12x^{2}+4x$。
(2) 原式$ = \frac{1}{3}a^{2}b^{3}-a^{2}b^{2}$。
(3) 原式$ = 9x^{3}y^{2}-3x^{2}y^{3}$。
(4) 原式$ = -12x^{4}+\frac{4}{3}x^{3}-3x^{2}$。

例2 如图所示，一块长方形硬纸片，长为$5a^{2}+4b^{2}$，宽为$6a^{4}$，在它的四个角上分别剪去一个边长为$\frac{3}{2}a^{3}$的小正方形，然后折成一个无盖的盒子，求这个无盖盒子的表面积。

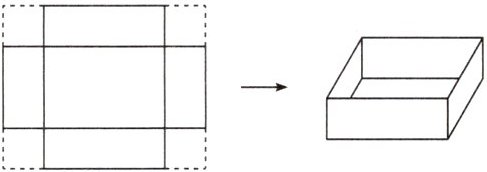
答案： 解：纸片的面积是$(5a^{2}+4b^{2})\cdot6a^{4}=30a^{6}+24a^{4}b^{2}$， 小正方形的面积是$(\frac{3}{2}a^{3})^{2}=\frac{9}{4}a^{6}$， 所以这个无盖盒子的表面积是$30a^{6}+24a^{4}b^{2}-4×\frac{9}{4}a^{6}=21a^{6}+24a^{4}b^{2}$。

3. 若三角形的底边长为$5m$，对应高为$2m - 1$，则此三角形的面积为 （ ）
A. $10m^{2}+5m$
B. $5m^{2}-1$
C. $10m^{2}-5m$
D. $5m^{2}-\frac{5}{2}m$

答案： D

4. 一段防洪堤坝的横断面是梯形，其上底为$a m$，下底为$(a + 2b)m$，坝高$2a m$。
（1）求这段防洪堤坝的横断面面积$S$。
（2）如果这段防洪堤坝长$200m$，那么这段防洪堤坝的体积是多少立方米？

答案： 解：
(1) $S=\frac{1}{2}\cdot2a\cdot(a + a + 2b)=a\cdot(2a + 2b)=(2a^{2}+2ab)(m^{2})$。
(2) $(2a^{2}+2ab)\cdot200=(400a^{2}+400ab)(m^{3})$。 所以这段防洪堤坝的体积是$(400a^{2}+400ab)m^{3}$。

1. （2024济南月考）某同学计算一个多项式乘$-3x^{2}$时，因抄错符号，算成了加上$-3x^{2}$，得到的答案是
$x^{2}-2x + 1$。
（1）求这个多项式；
（2）正确的计算结果应该是多少？

答案： 解：
(1) 这个多项式是$x^{2}-2x + 1-(-3x^{2})=x^{2}-2x + 1 + 3x^{2}=4x^{2}-2x + 1$。
(2) 正确的计算结果为$(4x^{2}-2x + 1)\cdot(-3x^{2})=-12x^{4}+6x^{3}-3x^{2}$。

2. 如图所示是用相同材料制作的A，B两种造型的长方形窗框，已知窗框的宽都是$x m$，长都是$y m$。
（1）制作这两种造型的窗框各一个，共需要多少材料？
（2）若一位用户需要A型的窗框5个，B型的窗框3个，且这种材料每米的价格为$a$元，这位用户共需要花多少钱（接缝处忽略不计）？

答案： 解：
(1) 根据题意，得制作一个A型窗框需要材料$(3x + 2y)m$，制作一个B型窗框需要材料$(2x + 3y)m$，则$(3x + 2y)+(2x + 3y)=(5x + 5y)(m)$， 即制作这两种造型的窗框各一个，共需要$(5x + 5y)m$的材料。
(2) 共需材料的长度为$5(3x + 2y)+3(2x + 3y)=15x + 10y + 6x + 9y=(21x + 19y)(m)$， $a(21x + 19y)=(21xa + 19ya)$（元）， 即这位用户共需要花$(21xa + 19ya)$元。