《2025年同步精练广东人民出版社七年级数学下册北师大版》

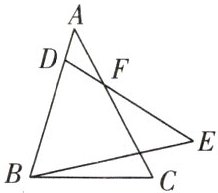
3. 如图所示，$BD = BC$，$BE = CA$，$\angle DBE = \angle C = 62^{\circ}$，$\angle BDE = 75^{\circ}$，则$\angle A$的度数等于______。

答案： 43°

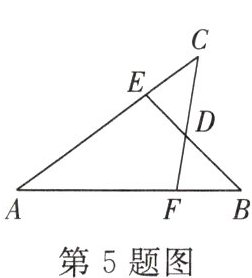
4. 如图所示，在$\triangle ABC$中，$D$是$BC$延长线上一点，满足$CD = BA$，过点$C$作$CE// AB$，且$CE = BC$，连接$DE$并延长，分别交$AC$，$AB$于点$F$，$G$。
（1）试说明$\angle D=\angle A$；
（2）若$BD = 12$，$AB = 8$，求$CE$的长。

答案： 解：
(1)因为CE//AB， 所以∠B = ∠ECD。 在△ABC与△DCE中，因为AB = DC，∠B = ∠ECD，BC = CE， 所以△ABC≌△DCE(SAS)。 所以∠D = ∠A。
(2)因为△ABC≌△DCE， 所以DC = AB = 8，CE = BC。 所以CE = BC = BD - DC = 12 - 8 = 4。

5. 如图所示，已知$AB = AC$，$AE = AF$，$BE$与$CF$交于点$D$，有下列结论：①$\triangle ABE\cong\triangle ACF$；②$\triangle BDF\cong\triangle CDE$；③点$D$在$\angle BAC$的平分线上。其中正确的是 （ ）

A. ①
B. ②
C. ①和②
D. ①②③

答案： D

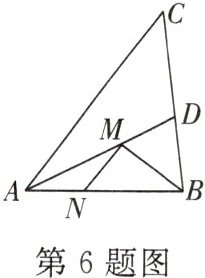
6. 如图所示，锐角三角形$ABC$的面积为$10$，$AC = 5$，$\angle BAC$的平分线交$BC$于点$D$，$M$，$N$分别是$AD$和$AB$上的动点，则$BM + MN$的最小值是______。

答案： 4

7. （2024深圳期末）【提出问题】仅用一把刻度尺，平分$\angle AOB$。

【设计方案】如图所示，已知$\angle AOB$，用刻度尺分别在$OA$，$OB$上截取$OC = OD$，$OE = OF$，连接$DE$，$CF$相交于点$G$，过点$O$，$G$作射线$OH$，则射线$OH$平分$\angle AOB$。

【解决问题】在$\triangle ODE$和$\triangle OCF$中，
$\begin{cases}OD = OC,\\(\ \ \ \ )=(\ \ \ \ )①,\\OE = OF,\end{cases}$
所以$\triangle ODE\cong\triangle OCF$（______）②，（填写全等的依据）
所以$\angle CEG=\angle DFG$。
因为$OC = OD$，$OE = OF$，
所以$OE - OC = OF - OD$，即______③。
又因为$\angle CEG=\angle DFG$，$\angle CGE=\angle DGF$，
所以______$\cong$______④，
所以______⑤。
又因为$OE = OF$，$\angle GEO=\angle GFO$，
所以$\triangle OEG\cong\triangle OFG(SAS)$，
所以______$=$______⑥，
即射线$OH$平分$\angle AOB$。

答案： \angle DOE@@\angle COF@@SAS@@CE = DF@@$\triangle CEG$@@$\triangle DFG$@@$EG = FG$@@$\angle EOG$@@$\angle FOG$

8. 如图所示，在$Rt\triangle ABC$中，$\angle ABC = 90^{\circ}$，$BD$是高，$E$是$\triangle ABC$外一点，$BE = BA$，$\angle E=\angle C$，若$DE = 5$，$AD = 12$，$BD\gt DE$，则$\triangle BDE$的面积为______。

答案： 30