《2025年同步精练广东人民出版社七年级数学下册北师大版》

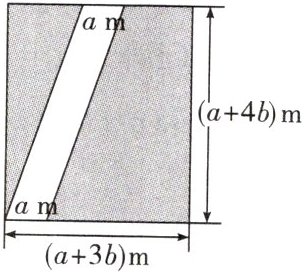
例2 为了更好地开展劳动教育，某学校暑期对学校闲置的地块进行规划改造，已知该地块（如图所示）是长为$(a + 4b)m$，宽为$(a + 3b)m$的长方形地块，学校准备在该地块内修一条平行四边形小路，小路的底边宽为$a m$，并计划将阴影部分改造为种植区。
（1）用含有$a$，$b$的式子分别表示出小路面积$S_{1}$和种植区的总面积$S_{2}$（结果化为最简）；
（2）若$a = 2$，$b = 4$，求出此时种植区的总面积$S_{2}$。

答案： 解：
(1) 由题意可得$S_{1}=a(a + 4b)=(a^{2}+4ab)(m^{2})$， $S_{2}=(a + 3b)(a + 4b)-(a^{2}+4ab)=a^{2}+4ab+3ab+12b^{2}-a^{2}-4ab=(3ab + 12b^{2})(m^{2})$。
(2) 当$a = 2$，$b = 4$时， $S_{2}=3ab + 12b^{2}=3×2×4+12×4^{2}=24 + 192=216(m^{2})$。

4. 一条水渠的横断面为梯形，它的上底为$a$，下底为$a + 2b$，高为$a - b$，则梯形的面积为 （ ）
A. $2a^{2}-2b^{2}$
B. $a^{2}-b^{2}$
C. $a^{2}-2b^{2}$
D. $\frac{1}{2}a^{2}-\frac{1}{2}b^{2}$

答案： B

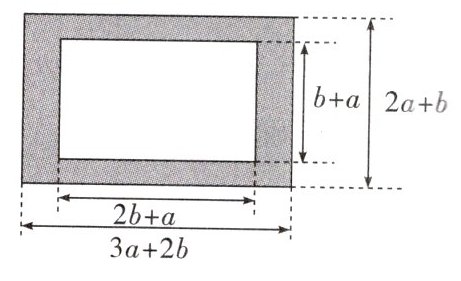
5. 计算图中阴影部分的面积。

答案： 解：大长方形的面积为$(3a + 2b)(2a + b)=6a^{2}+7ab+2b^{2}$， 小长方形的面积为$(2b + a)(b + a)=a^{2}+3ab+2b^{2}$， 所以阴影部分的面积为$(3a + 2b)(2a + b)-(2b + a)(b + a)=(6a^{2}+7ab+2b^{2})-(a^{2}+3ab+2b^{2})=5a^{2}+4ab$。

1. （2024郑州期末）观察图（1）中多项式乘多项式的运算规律，将之迁移到如图（2）所示的运算中，可得$m$，$n(m\lt n)$分别是 （ ）


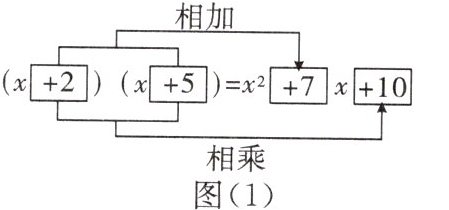
A. $-5$，$-2$
B. $-5$，$2$
C. $-2$，$5$
D. $5$，$2$

答案： B

2. [代数推理]李老伯把一块长为$a m$，宽为$b m$（$a\gt b\gt100$）的长方形土地租给租户张老伯，第二年，他对张老伯说：“我把这块地的长增加$10 m$，宽减少$10 m$，继续租给你，租金不变，你也没有吃亏，你看如何？”你觉得张老伯的租地面积会 （ ）

A. 变小了
B. 变大了
C. 没有变化
D. 无法确定

答案： A

3. 已知多项式$(x^{2}+px + q)(x^{2}-3x + 2)$的结果中不含$x^{3}$项和$x^{2}$项，求$p$和$q$的值。

答案： 解：因为$(x^{2}+px + q)(x^{2}-3x + 2)=x^{4}-3x^{3}+2x^{2}+px^{3}-3px^{2}+2px+qx^{2}-3qx + 2q=x^{4}-(3 - p)x^{3}+(2 - 3p + q)x^{2}+2px-3qx + 2q$。 因为多项式$(x^{2}+px + q)(x^{2}-3x + 2)$的结果中不含$x^{3}$项和$x^{2}$项， 所以$3 - p = 0$，$2 - 3p + q = 0$， 解得$p = 3$，$q = 7$。