《2025年同步精练广东人民出版社七年级数学下册北师大版》

4. 在同一平面内，直线 $AB$ 与直线 $CD$ 相交于点 $O$，$\angle AOC = 30^{\circ}$，射线 $OE\perp CD$，则 $\angle BOE$ 的度数为 ______________。

答案： 60°或120°

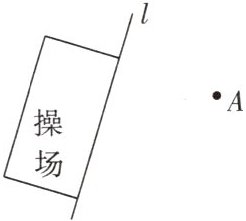
5.（1）如图所示，教学楼 $A$ 位于学校操场的一侧，为了节省学生课间到操场的时间，学校想修一条道路 $AO$（$O$ 在直线 $l$ 上），使得学生走到操场的距离最短，学校该如何修路？（只需在图中画出）
（2）请再举出两条日常生活中应用“垂线段最短”的例子。

答案： 解：
(1)过点A作直线l的垂线即可，图略。
(2)答案不唯一，如：①测量跳远成绩；②从河流引水浇远处的庄稼。

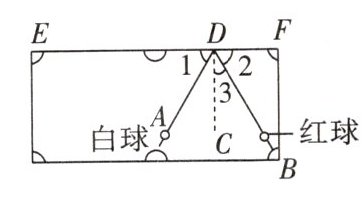
6. [教材习题变式]如图所示，打台球时，选择适当的方向击打白球，白球反弹后击中红球，红球会直接入袋。已知 $CD\perp EF$，$\angle 1 = 60^{\circ}$。
（1）要想白球反弹后能击中红球，则 $\angle 2$ 的度数为 ________；此时 $\angle 3 =$ ________ $^{\circ}$；
（2）直接写出与 $\angle 3$ 的度数大小相等的角。

答案： 60°@@30@@
(2)与∠3相等的角有∠ADC，∠DBF。

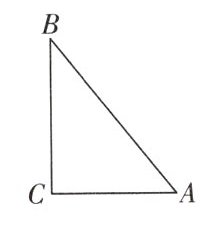
7. 如图所示，点 $A$ 表示小雨家，点 $B$ 表示小樱家，点 $C$ 表示小丽家，她们三家恰好组成了一个直角三角形，其中 $AC\perp BC$，$AC = 900$ 米，$BC = 1200$ 米，$AB = 1500$ 米。
（1）试说出小雨家到街道 $BC$ 的距离以及小樱家到街道 $AC$ 的距离。
（2）画出表示小丽家到街道 $AB$ 距离的线段。

答案：
解：
(1)因为AC⊥BC，AC = 900米，BC = 1200米， 所以小雨家到街道BC的距离为900米，小樱家到街道AC的距离为1200米。
(2)如图所示，CD即为小丽家到街道AB距离的线段。

8.（2024 汕头期中）如图所示，直线 $AB$、$CD$ 相交于点 $O$，$OE\perp AB$，$OF$ 平分 $\angle AOD$。
（1）若 $\angle COE = 50^{\circ}$，求 $\angle AOF$ 的度数；
（2）若 $\angle COE:\angle AOF = 2:3$，求 $\angle BOD$ 的度数。

答案： 解：因为OE⊥AB，所以∠AOE = 90°。 因为∠COE = 50°，所以∠AOC = 40°， 所以∠AOD = 180° - ∠AOC = 140°。 因为OF平分∠AOD， 所以∠AOF = $\frac{1}{2}$∠AOD = $\frac{1}{2}$×140° = 70°。
(2)因为OE⊥AB，所以∠AOE = 90°。 因为∠COE：∠AOF = 2：3， 设∠COE = 2x°，则∠AOF = 3x°， 所以∠AOC = (90 - 2x)°。 因为OF平分∠AOD， 所以∠AOD = 2∠AOF = 6x°。 因为∠AOC + ∠AOD = 180°， 所以90 - 2x + 6x = 180，解得x = $\frac{45}{2}$， 所以∠BOD = ∠AOC = (90 - 2x)° = 90° - 2×$\frac{45}{2}$ = 45°。