《2025年同步精练广东人民出版社七年级数学下册北师大版》

1.（2024 湛江期末）如图所示，一副三角尺（直角顶点重合）摆放在桌面上，若$\angle AOD = 160^{\circ}$，则$\angle BOC$等于（ ）

A. $20^{\circ}$
B. $30^{\circ}$
C. $40^{\circ}$
D. $50^{\circ}$

答案： A

2.（2024 高州月考）若一个角的度数是$50^{\circ}$，则它的余角的度数是（ ）
A. $140^{\circ}$
B. $40^{\circ}$
C. $130^{\circ}$
D. $30^{\circ}$

答案： B

3.（2024 阳江期中）如图所示，直线$AB$，$CD$相交于点$O$，$OE$平分$\angle BOD$。
（1）若$\angle BOD = 68^{\circ}$，$\angle DOF = 90^{\circ}$，求$\angle EOF$的度数；
（2）若$OF$平分$\angle COE$，$\angle BOF = 30^{\circ}$，求$\angle BOD$的度数。

答案： 解：（1）因为∠DOF = 90°，∠BOD = 68°， 所以∠BOF = ∠DOF - ∠BOD = 90° - 68° = 22°。 因为OE平分∠BOD， 所以∠BOE = 1/2∠BOD = 34°， 所以∠EOF = ∠BOF + ∠BOE = 22° + 34° = 56°。 （2）因为OE平分∠BOD， 所以∠BOE = ∠DOE = 1/2∠BOD， 所以∠COE = 180° - ∠DOE = 180° - 1/2∠BOD。 因为OF平分∠COE， 所以∠EOF = 1/2∠COE = 1/2(180° - 1/2∠BOD) = 90° - 1/4∠BOD。 因为∠BOF = ∠EOF - ∠BOE， 所以30° = 90° - 1/4∠BOD - 1/2∠BOD， 所以∠BOD = 80°。

4.（2024 青海）如图所示，一个弯曲管道$AB// CD$，$\angle ABC = 120^{\circ}$，则$\angle BCD$的度数是（ ）

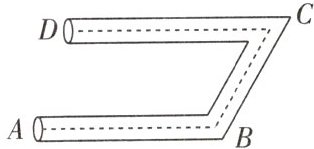
A. $120^{\circ}$
B. $30^{\circ}$
C. $60^{\circ}$
D. $150^{\circ}$

答案： C

5.（2024 南充）如图所示，两个平面镜平行放置，光线经过平面镜反射时，$\angle 1 = \angle 2 = 40^{\circ}$，则$\angle 3$的度数为（ ）

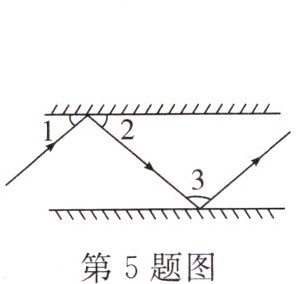
A. $80^{\circ}$
B. $90^{\circ}$
C. $100^{\circ}$
D. $120^{\circ}$

答案： C

6.（2024 通辽）将三角尺$ABC$按如图所示位置摆放，顶点$A$落在直线$l_1$上，顶点$B$落在直线$l_2$上，若$l_1// l_2$，$\angle 1 = 25^{\circ}$，则$\angle 2$的度数是（ ）

A. $45^{\circ}$
B. $35^{\circ}$
C. $30^{\circ}$
D. $25^{\circ}$

答案： B

7.（2024 达州）当光线从空气射入水中时，光线的传播方向发生了改变，这就是光的折射现象（如图所示）。图中$\angle 1 = 80^{\circ}$，$\angle 2 = 40^{\circ}$，则$\angle 3$的度数为（ ）

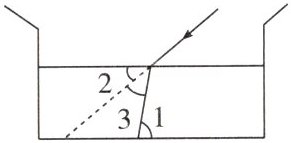
A. $30^{\circ}$
B. $40^{\circ}$
C. $50^{\circ}$
D. $70^{\circ}$

答案： B

8.（2024 潮州月考）完成下面的证明：已知，如图所示，$AB// CD// GH$，$EG$平分$\angle BEF$，$FG$平分$\angle EFD$。求证：$\angle EGF = 90^{\circ}$。
证明：因为$HG// AB$（已知），
所以$\angle 1 =$ _______（_______）。
又因为$HG// CD$（已知），
所以$\angle 2 = \angle 4$。
因为$AB// CD$（已知），
所以$\angle BEF +$ _______$ = 180^{\circ}$（_______）。
又因为$EG$平分$\angle BEF$（已知），
所以$\angle 1 = \frac{1}{2}\angle$ _______。
又因为$FG$平分$\angle EFD$（已知），
所以$\angle 2 = \frac{1}{2}\angle$ _______，
所以$\angle 1 + \angle 2 = \frac{1}{2}$（_______），
所以$\angle 1 + \angle 2 = 90^{\circ}$，
所以$\angle 3 + \angle 4 = 90^{\circ}$（_______），
即$\angle EGF = 90^{\circ}$。

答案： ∠3@@两直线平行，内错角相等@@∠DFE@@两直线平行，同旁内角互补@@BEF@@DFE@@∠BEF + ∠DFE@@等量代换