第95页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
1. 新考法 分类讨论法 如图,一次函数$y = \frac{3}{4}x + 6$的图象与$x$轴交于点$A$,与$y$轴交于点$B$,$OC\perp AB$于点$C$,点$P$在直线$AB$上运动,点$Q$在$y$轴的正半轴上运动.
(1)求点$A$,$B$的坐标;
(2)求$OC$的长;
(3)若以$O$,$P$,$Q$为顶点的三角形与$\triangle OCP$全等,求点$Q$的坐标.

(1)求点$A$,$B$的坐标;
(2)求$OC$的长;
(3)若以$O$,$P$,$Q$为顶点的三角形与$\triangle OCP$全等,求点$Q$的坐标.

答案:
【解】
(1)在$y = \frac{3}{4}x + 6$中,令$x = 0$,得$y = 6$;令$y = 0$,得$x = - 8$。 $\therefore A(-8,0)$,$B(0,6)$。
(2)由
(1)知$A(-8,0)$,$B(0,6)$, $\therefore OA = 8$,$OB = 6$, $\therefore AB=\sqrt{OA^{2}+OB^{2}} = 10$。 $\because S_{\triangle AOB}=\frac{1}{2}OA\cdot OB=\frac{1}{2}AB\cdot OC$, $\therefore OC=\frac{OA\cdot OB}{AB}=\frac{8\times6}{10}=\frac{24}{5}$。
(3)$\because$以$O$,$P$,$Q$为顶点的三角形与$\triangle OCP$全等, $\therefore OP$是$\triangle POQ$的斜边,$Q$为直角顶点。 设$P(m,\frac{3}{4}m + 6)$,则易得$Q(0,\frac{3}{4}m + 6)$。 当$\triangle OCP\cong\triangle PQO$,$P$在$C$下方时,如图①, 则$OC = PQ$,$\therefore PQ=\frac{24}{5}$,$\therefore m = -\frac{24}{5}$, $\therefore\frac{3}{4}m + 6=\frac{3}{4}\times(-\frac{24}{5})+6=\frac{12}{5}$,$\therefore Q(0,\frac{12}{5})$; 当$\triangle OCP\cong\triangle PQO$,$P$在$B$上方时,如图②。 $\because PQ = OC$,$\therefore PQ=\frac{24}{5}$,$\therefore m=\frac{24}{5}$, $\therefore\frac{3}{4}m + 6=\frac{3}{4}\times\frac{24}{5}+6=\frac{48}{5}$,$\therefore Q(0,\frac{48}{5})$; 当$\triangle OCP\cong\triangle OQP$,$P$在$C$,$B$之间时,如图③, 则$OQ = OC=\frac{24}{5}$,$\therefore Q(0,\frac{24}{5})$。 综上所述,点$Q$的坐标为$(0,\frac{12}{5})$或$(0,\frac{48}{5})$或$(0,\frac{24}{5})$。
【解】
(1)在$y = \frac{3}{4}x + 6$中,令$x = 0$,得$y = 6$;令$y = 0$,得$x = - 8$。 $\therefore A(-8,0)$,$B(0,6)$。
(2)由
(1)知$A(-8,0)$,$B(0,6)$, $\therefore OA = 8$,$OB = 6$, $\therefore AB=\sqrt{OA^{2}+OB^{2}} = 10$。 $\because S_{\triangle AOB}=\frac{1}{2}OA\cdot OB=\frac{1}{2}AB\cdot OC$, $\therefore OC=\frac{OA\cdot OB}{AB}=\frac{8\times6}{10}=\frac{24}{5}$。
(3)$\because$以$O$,$P$,$Q$为顶点的三角形与$\triangle OCP$全等, $\therefore OP$是$\triangle POQ$的斜边,$Q$为直角顶点。 设$P(m,\frac{3}{4}m + 6)$,则易得$Q(0,\frac{3}{4}m + 6)$。 当$\triangle OCP\cong\triangle PQO$,$P$在$C$下方时,如图①, 则$OC = PQ$,$\therefore PQ=\frac{24}{5}$,$\therefore m = -\frac{24}{5}$, $\therefore\frac{3}{4}m + 6=\frac{3}{4}\times(-\frac{24}{5})+6=\frac{12}{5}$,$\therefore Q(0,\frac{12}{5})$; 当$\triangle OCP\cong\triangle PQO$,$P$在$B$上方时,如图②。 $\because PQ = OC$,$\therefore PQ=\frac{24}{5}$,$\therefore m=\frac{24}{5}$, $\therefore\frac{3}{4}m + 6=\frac{3}{4}\times\frac{24}{5}+6=\frac{48}{5}$,$\therefore Q(0,\frac{48}{5})$; 当$\triangle OCP\cong\triangle OQP$,$P$在$C$,$B$之间时,如图③, 则$OQ = OC=\frac{24}{5}$,$\therefore Q(0,\frac{24}{5})$。 综上所述,点$Q$的坐标为$(0,\frac{12}{5})$或$(0,\frac{48}{5})$或$(0,\frac{24}{5})$。

2. 新视角 存在性探究题 如图,在平面直角坐标系中,正比例函数$y = kx(k\neq0)$与一次函数$y = -x + 7$的图象相交于点$A(t,3)$,过点$P(0,4)$作$x$轴的平行线,交$y = kx$的图象于点$B$,交$y = -x + 7$的图象于点$C$,连接$OC$.
(1)求$t$与$k$的值.
(2)求$\triangle OBC$的面积.
(3)在$x$轴上是否存在点$M$,使$\triangle AOM$是以$OA$为腰的等腰三角形?若存在,求出所有点$M$的坐标;若不存在,请说明理由.
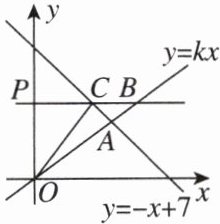
(1)求$t$与$k$的值.
(2)求$\triangle OBC$的面积.
(3)在$x$轴上是否存在点$M$,使$\triangle AOM$是以$OA$为腰的等腰三角形?若存在,求出所有点$M$的坐标;若不存在,请说明理由.

答案:
【解】
(1)把点$A(t,3)$的坐标代入一次函数$y = - x + 7$, 得$3 = - t + 7$, 解得$t = 4$,$\therefore A(4,3)$。 把$A(4,3)$的坐标代入正比例函数$y = kx(k\neq0)$,得$4k = 3$, $\therefore k=\frac{3}{4}$。
(2)$\because PC// x$轴,$P(0,4)$, $\therefore$把$y = 4$代入$y=\frac{3}{4}x$中, 解得$x=\frac{16}{3}$,$\therefore B(\frac{16}{3},4)$。 把$y = 4$代入$y = - x + 7$中,解得$x = 3$, $\therefore C(3,4)$,$\therefore BC=\frac{16}{3}-3=\frac{7}{3}$。 $\because P(0,4)$,$\therefore OP = 4$。 $\therefore S_{\triangle PBC}=\frac{1}{2}BC\cdot OP=\frac{1}{2}\times\frac{7}{3}\times4=\frac{14}{3}$。
(3)存在。 设点$M$的坐标为$(m,0)$。 $\because A(4,3)$,$\therefore$易知$AO=\sqrt{4^{2}+3^{2}} = 5$。 $\because\triangle AOM$是以$OA$为腰的等腰三角形, $\therefore$分及两种情况考虑: 当$AO = OM$时,有$5 = |m|$,解得$m=\pm5$, $\therefore$点$M$的坐标为$(-5,0)$或$(5,0)$; 当$AO = AM$时,有$5=\sqrt{(m - 4)^{2}+3^{2}}$, 解得$m_1 = 8$,$m_2 = 0$(舍去)。 $\therefore$点$M$的坐标为$(-5,0)$或$(5,0)$或$(8,0)$。
(1)把点$A(t,3)$的坐标代入一次函数$y = - x + 7$, 得$3 = - t + 7$, 解得$t = 4$,$\therefore A(4,3)$。 把$A(4,3)$的坐标代入正比例函数$y = kx(k\neq0)$,得$4k = 3$, $\therefore k=\frac{3}{4}$。
(2)$\because PC// x$轴,$P(0,4)$, $\therefore$把$y = 4$代入$y=\frac{3}{4}x$中, 解得$x=\frac{16}{3}$,$\therefore B(\frac{16}{3},4)$。 把$y = 4$代入$y = - x + 7$中,解得$x = 3$, $\therefore C(3,4)$,$\therefore BC=\frac{16}{3}-3=\frac{7}{3}$。 $\because P(0,4)$,$\therefore OP = 4$。 $\therefore S_{\triangle PBC}=\frac{1}{2}BC\cdot OP=\frac{1}{2}\times\frac{7}{3}\times4=\frac{14}{3}$。
(3)存在。 设点$M$的坐标为$(m,0)$。 $\because A(4,3)$,$\therefore$易知$AO=\sqrt{4^{2}+3^{2}} = 5$。 $\because\triangle AOM$是以$OA$为腰的等腰三角形, $\therefore$分及两种情况考虑: 当$AO = OM$时,有$5 = |m|$,解得$m=\pm5$, $\therefore$点$M$的坐标为$(-5,0)$或$(5,0)$; 当$AO = AM$时,有$5=\sqrt{(m - 4)^{2}+3^{2}}$, 解得$m_1 = 8$,$m_2 = 0$(舍去)。 $\therefore$点$M$的坐标为$(-5,0)$或$(5,0)$或$(8,0)$。
3. 新视角 动点探究题 如图①,在平面直角坐标系中,一次函数$y = kx + b$分别与$x$轴和$y$轴交于点$A$和点$B$,$OA = OB = 6$.
(1)直线$l$经过$AB$两点,求直线$AB$的表达式.
(2)以$AB$为腰,$B$为直角顶点,在第一象限构造等腰直角三角形$ABC$,求$BC$所在直线的表达式.
(3)如图②,$P$为点$A$右侧$x$轴上的一动点,以$P$为直角顶点,$BP$为腰在第一象限内作等腰直角三角形$BPQ$,连接$QA$并延长交$y$轴于点$K$. 当点$P$运动时,点$K$的位置是否发生变化?如果不变,请求出它的坐标;如果变化,请说明理由.

(1)直线$l$经过$AB$两点,求直线$AB$的表达式.
(2)以$AB$为腰,$B$为直角顶点,在第一象限构造等腰直角三角形$ABC$,求$BC$所在直线的表达式.
(3)如图②,$P$为点$A$右侧$x$轴上的一动点,以$P$为直角顶点,$BP$为腰在第一象限内作等腰直角三角形$BPQ$,连接$QA$并延长交$y$轴于点$K$. 当点$P$运动时,点$K$的位置是否发生变化?如果不变,请求出它的坐标;如果变化,请说明理由.

答案:
【解】
(1)$\because OA = OB = 6$,$\therefore A(6,0)$,$B(0,6)$。 设直线$AB$的表达式为$y = kx + 6$, $\therefore 0 = 6k + 6$,解得$k = - 1$, $\therefore$直线$AB$的表达式为$y = - x + 6$。
(2)如图①,过点$C$作$CF\perp y$轴于点$F$。 $\because\triangle ABC$是等腰直角三角形, $\therefore\angle ABC = 90^{\circ}$,$AB = BC$, $\therefore\angle ABO = 90^{\circ}-\angle FBC=\angle BCF$。 又$\because\angle BFC=\angle AOB = 90^{\circ}$, $\therefore\triangle BFC\cong\triangle AOB(AAS)$, $\therefore CF = OB = 6$,$BF = AO = 6$, $\therefore OF = 12$,$\therefore C(6,12)$。 同
(1)易知$BC$所在直线的表达式为$y = x + 6$。
(3)点$K$的位置不发生变化。 如图②,过点$Q$作$QH\perp x$轴于点$H$。 $\because\triangle BPQ$是等腰直角三角形,$\angle BPQ = 90^{\circ}$, $\therefore BP = QP$, $\therefore\angle OPB+\angle HPQ = 90^{\circ}$。 又$\because\angle OPB+\angle OBP = 90^{\circ}$, $\therefore\angle OBP=\angle HPQ$。 又$\because\angle BOP=\angle PHQ = 90^{\circ}$,$BP = QP$, $\therefore\triangle BOP\cong\triangle PHQ(AAS)$, $\therefore OB = PH$,$OP = QH$, $\therefore PH + PO = BO + OP$,$\therefore OA + AH = BO + QH$。 又$\because OA = OB$, $\therefore AH = QH$, $\therefore\triangle AHQ$是等腰直角三角形, $\therefore\angle QAH = 45^{\circ}$,$\therefore\angle OAK = 45^{\circ}$, $\therefore\triangle OAK$为等腰直角三角形, $\therefore OK = OA = 6$,$\therefore K(0,-6)$。

【解】
(1)$\because OA = OB = 6$,$\therefore A(6,0)$,$B(0,6)$。 设直线$AB$的表达式为$y = kx + 6$, $\therefore 0 = 6k + 6$,解得$k = - 1$, $\therefore$直线$AB$的表达式为$y = - x + 6$。
(2)如图①,过点$C$作$CF\perp y$轴于点$F$。 $\because\triangle ABC$是等腰直角三角形, $\therefore\angle ABC = 90^{\circ}$,$AB = BC$, $\therefore\angle ABO = 90^{\circ}-\angle FBC=\angle BCF$。 又$\because\angle BFC=\angle AOB = 90^{\circ}$, $\therefore\triangle BFC\cong\triangle AOB(AAS)$, $\therefore CF = OB = 6$,$BF = AO = 6$, $\therefore OF = 12$,$\therefore C(6,12)$。 同
(1)易知$BC$所在直线的表达式为$y = x + 6$。
(3)点$K$的位置不发生变化。 如图②,过点$Q$作$QH\perp x$轴于点$H$。 $\because\triangle BPQ$是等腰直角三角形,$\angle BPQ = 90^{\circ}$, $\therefore BP = QP$, $\therefore\angle OPB+\angle HPQ = 90^{\circ}$。 又$\because\angle OPB+\angle OBP = 90^{\circ}$, $\therefore\angle OBP=\angle HPQ$。 又$\because\angle BOP=\angle PHQ = 90^{\circ}$,$BP = QP$, $\therefore\triangle BOP\cong\triangle PHQ(AAS)$, $\therefore OB = PH$,$OP = QH$, $\therefore PH + PO = BO + OP$,$\therefore OA + AH = BO + QH$。 又$\because OA = OB$, $\therefore AH = QH$, $\therefore\triangle AHQ$是等腰直角三角形, $\therefore\angle QAH = 45^{\circ}$,$\therefore\angle OAK = 45^{\circ}$, $\therefore\triangle OAK$为等腰直角三角形, $\therefore OK = OA = 6$,$\therefore K(0,-6)$。


查看更多完整答案,请扫码查看


