《2025年综合应用创新题典中点七年级数学下册鲁教版五四制》

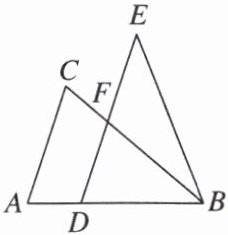
9. [2024·青岛高新区模拟] 如图，在△ABC中，AB＞AC，点D在边AB上，且BD = CA，过点D作DE//AC交BC于点F，连接BE，且∠DFB = ∠ABE，求证：△ABC≌△DEB.

答案： 【证明】因为DE//AC，所以∠A = ∠BDE，∠C = ∠DFB。 因为∠DFB = ∠ABE，所以∠C = ∠DBE。 在△ABC和△DEB中，$\begin{cases}  ∠C = ∠DBE \\ AC = BD \\ ∠A = ∠BDE  \end{cases}$所以△ABC≌△DEB（ASA）。

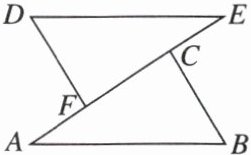
10. 新视角 开放题 如图，A，F，C，E在同一直线上，AB//DE，AF = CE，在下列四个条件：①∠A = ∠E；②∠B = ∠D；③DF//BC；④BC = DF中，选择一个合适的条件证明△ABC与△EDF全等.

答案： 【解】选②∠B = ∠D。 证明：因为AB//DE，所以∠A = ∠E， 因为AF = CE，所以AF + FC = CE + FC，即AC = EF， 在△ABC和△EDF中，$\begin{cases}∠B = ∠D \\ ∠A = ∠E \\ AC = EF \end{cases}$ 所以△ABC≌△EDF（AAS）。 选③DF//BC。 证明：因为AB//DE，所以∠A = ∠E。 因为AF = CE，所以AF + FC = CE + FC，即AC = EF。 因为DF//BC，所以∠DFE = ∠BCA。 在△ABC和△EDF中，$\begin{cases} ∠BCA = ∠DFE \\ AC = EF \\ ∠A = ∠E  \end{cases}$ 所以△ABC≌△EDF（ASA）。（任选其一）

11. 如图，把一张长方形纸片ABCD折叠，使点C与点A重合，折痕为EF.
(1)如果∠DEF = 120°，求∠BAF的度数；
(2)判断△ABF和△AGE是否全等，请说明理由.

答案： 【解】（1）因为四边形ABCD是长方形，所以AD//BC， 所以∠CFE = 180° - ∠DEF = 60°。由折叠知，∠AFE = ∠CFE = 60°，所以∠AFB = 180° - ∠AFE - ∠CFE = 60°。 因为∠B = 90°，所以∠BAF = 90° - ∠AFB = 30°。 （2）△ABF≌△AGE。理由：由折叠知，AG = CD，∠G = ∠D = 90°，∠GAF = ∠C = 90°。因为∠B = 90°，AB = CD， 所以∠B = ∠G，AB = AG。因为∠BAD = 90°，∠GAF = 90°， 所以∠BAD - ∠EAF = ∠GAF - ∠EAF，即∠BAF = ∠GAE。 在△ABF和△AGE中，$\begin{cases}∠B = ∠G = 90° \\ AB = AC \\ ∠BAF = ∠GAE  \end{cases}$ 所以△ABF≌△AGE（ASA）。

12. 如图，AB = 8 cm，AC = BD = 5 cm，∠CAB = ∠DBA = 60°，点P在线段AB上以1 cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动. 它们运动的时间为t s，当点Q的运动速度为多少时，A，C，P三点构成的三角形与B，P，Q三点构成的三角形全等？

答案： 【解】设点Q的运动速度为x cm/s，则AP = t cm，BQ = xt cm，所以BP = AB - AP = (8 - t)cm。 因为∠CAB = ∠DBA = 60°， 所以可分两种情况讨论：①当AP = BQ，AC = BP，即△ACP≌△BPQ时， 所以t = xt，5 = 8 - t，解得t = 3，x = 1； ②当AP = BP，AC = BQ，即△ACP≌△BQP时， 所以t = 8 - t，5 = xt，解得t = 4，x = $\frac{5}{4}$。 综上可知，当点Q的运动速度为1 cm/s或$\frac{5}{4}$ cm/s时，A，C，P三点构成的三角形与B，P，Q三点构成的三角形全等。