《2025年综合应用创新题典中点七年级数学下册鲁教版五四制》

10. [2024·广州白云区期末] 完成下面的证明：
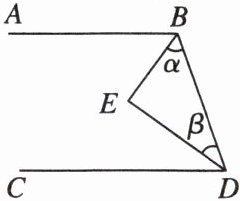
如图，BE平分∠ABD，DE平分∠BDC，且∠α + ∠β = 90°.
求证：AB//CD.

答案： 【证明】
∵BE 平分∠ABD，
∴∠ABD = 2∠α.
∵DE 平分∠BDC，
∴∠BDC = 2∠β.
∴∠ABD + ∠BDC = 2∠α + 2∠β = 2(∠α + ∠β).
∵∠α + ∠β = 90°，
∴∠ABD + ∠BDC = 180°.
∴AB//CD.

11. 如图，已知AF平分∠BAC，DE平分∠BDF，且∠BDE = ∠CAF.
（1）DF与AC平行吗？为什么？
（2）请判断DE与AF的位置关系，并说明理由.

答案： 【解】
(1)DF//AC，理由如下：
∵AF 平分∠BAC，DE 平分∠BDF，
∴∠BAC = 2∠CAF，∠BDF = 2∠BDE. 又
∵∠BDE = ∠CAF，
∴∠BDF = ∠BAC，
∴DF//AC.
(2)DE//AF，理由如下：
∵AF 平分∠BAC，
∴∠BAF = ∠CAF. 又
∵∠BDE = ∠CAF，
∴∠BDE = ∠BAF.
∴DE//AF.

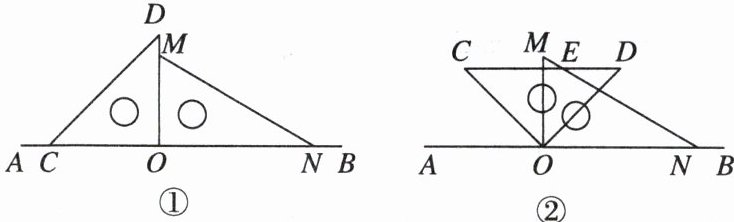
12. 新考法 分类讨论法 如图，将一副直角三角板放在同一条直线上，其中∠ONM = 30°，∠OCD = 45°.
（1）将图①中的三角板OCD绕点O按顺时针方向旋转，使一边OD在∠MON的内部，如图②，且OD恰好平分∠MON，CD与MN相交于点E，求∠CEN的度数.
（2）将图①中的三角板OCD绕点O按5°/s的速度沿顺时针方向旋转一周，在旋转过程中，在第几秒时，边CD恰好与边MN平行？

答案：
【解】
(1)当 OD 平分∠MON 时，∠DON = 45°. 由题意知∠D = 45°.
∴∠D = ∠DON.
∴CD//ON.
∴∠CEN + ∠MNO = 180°. 又
∵∠MNO = 30°，
∴∠CEN = 150°.
(2)①如图①，当 CD 在直线 AB 上方时，设 OD 交 MN 于 F.
∵CD//MN，
∴∠OFM = ∠D = 45°.
∵∠OFM = 180° - ∠OFN = ∠MNO + ∠FON，
∴∠FON = 45° - 30° = 15°.
∴∠MOF = 75°. 此时三角尺 OCD 旋转了 75°. 75°÷5° = 15(s)；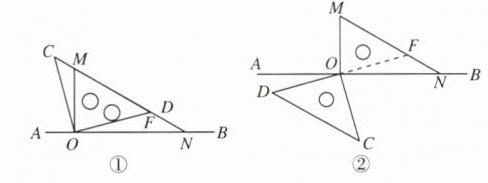
②如图②，当 CD 在直线 AB 下方时，延长 DO 交 MN 于 F. 同理可得∠MOF = 75°. 此时三角尺 OCD 旋转了 75° + 180° = 255°. 255°÷5° = 51(s). 综上，在第 15 s 或第 51 s 时，边 CD 恰好与边 MN 平行.